Neural PDE Solvers for Irregular Domains

Neural network-based approaches for solving partial differential equations (PDEs) have recently received special attention. However, the large majority of neural PDE solvers only apply to rectilinear domains, and do not systematically address the imposition of Dirichlet/Neumann boundary conditions over irregular domain boundaries. In this paper, we present a framework to neurally solve partial differential equations over domains with irregularly shaped (non-rectilinear) geometric boundaries. Our network takes in the shape of the domain as an input (represented using an unstructured point cloud, or any other parametric representation such as Non-Uniform Rational B-Splines) and is able to generalize to novel (unseen) irregular domains; the key technical ingredient to realizing this model is a novel approach for identifying the interior and exterior of the computational grid in a differentiable manner. We also perform a careful error analysis which reveals theoretical insights into several sources of error incurred in the model-building process. Finally, we showcase a wide variety of applications, along with favorable comparisons with ground truth solutions.

NeuFENet: Neural Finite Element Solutions with Theoretical Bounds for Parametric PDEs

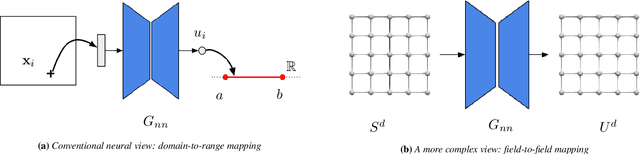
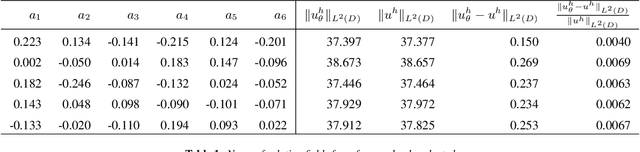
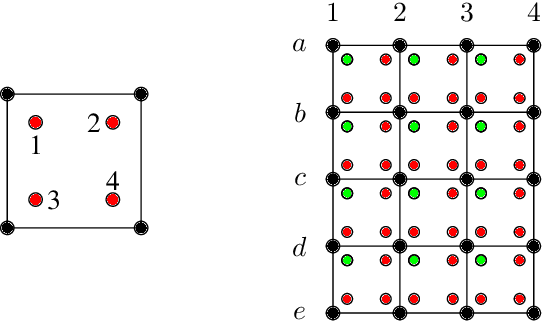
We consider a mesh-based approach for training a neural network to produce field predictions of solutions to parametric partial differential equations (PDEs). This approach contrasts current approaches for "neural PDE solvers" that employ collocation-based methods to make point-wise predictions of solutions to PDEs. This approach has the advantage of naturally enforcing different boundary conditions as well as ease of invoking well-developed PDE theory -- including analysis of numerical stability and convergence -- to obtain capacity bounds for our proposed neural networks in discretized domains. We explore our mesh-based strategy, called NeuFENet, using a weighted Galerkin loss function based on the Finite Element Method (FEM) on a parametric elliptic PDE. The weighted Galerkin loss (FEM loss) is similar to an energy functional that produces improved solutions, satisfies a priori mesh convergence, and can model Dirichlet and Neumann boundary conditions. We prove theoretically, and illustrate with experiments, convergence results analogous to mesh convergence analysis deployed in finite element solutions to PDEs. These results suggest that a mesh-based neural network approach serves as a promising approach for solving parametric PDEs with theoretical bounds.

Differentiable Spline Approximations

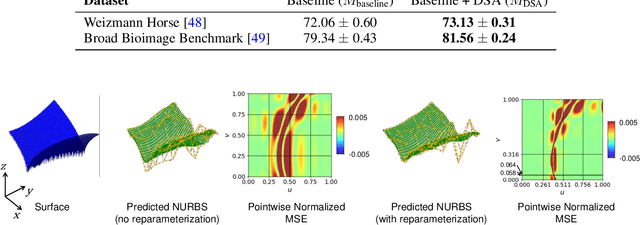
The paradigm of differentiable programming has significantly enhanced the scope of machine learning via the judicious use of gradient-based optimization. However, standard differentiable programming methods (such as autodiff) typically require that the machine learning models be differentiable, limiting their applicability. Our goal in this paper is to use a new, principled approach to extend gradient-based optimization to functions well modeled by splines, which encompass a large family of piecewise polynomial models. We derive the form of the (weak) Jacobian of such functions and show that it exhibits a block-sparse structure that can be computed implicitly and efficiently. Overall, we show that leveraging this redesigned Jacobian in the form of a differentiable "layer" in predictive models leads to improved performance in diverse applications such as image segmentation, 3D point cloud reconstruction, and finite element analysis.

Distributed Multigrid Neural Solvers on Megavoxel Domains

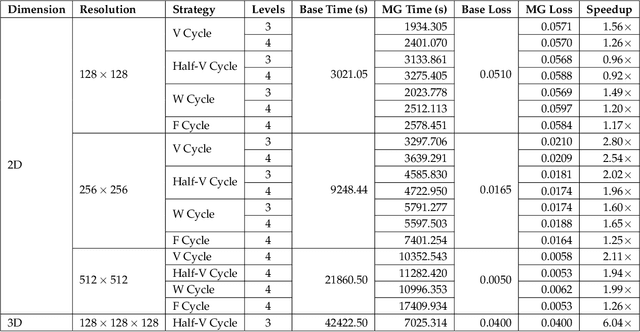
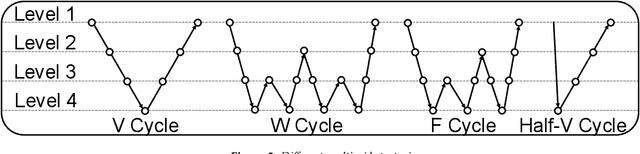
We consider the distributed training of large-scale neural networks that serve as PDE solvers producing full field outputs. We specifically consider neural solvers for the generalized 3D Poisson equation over megavoxel domains. A scalable framework is presented that integrates two distinct advances. First, we accelerate training a large model via a method analogous to the multigrid technique used in numerical linear algebra. Here, the network is trained using a hierarchy of increasing resolution inputs in sequence, analogous to the 'V', 'W', 'F', and 'Half-V' cycles used in multigrid approaches. In conjunction with the multi-grid approach, we implement a distributed deep learning framework which significantly reduces the time to solve. We show the scalability of this approach on both GPU (Azure VMs on Cloud) and CPU clusters (PSC Bridges2). This approach is deployed to train a generalized 3D Poisson solver that scales well to predict output full-field solutions up to the resolution of 512x512x512 for a high dimensional family of inputs.

Deep Generative Models that Solve PDEs: Distributed Computing for Training Large Data-Free Models

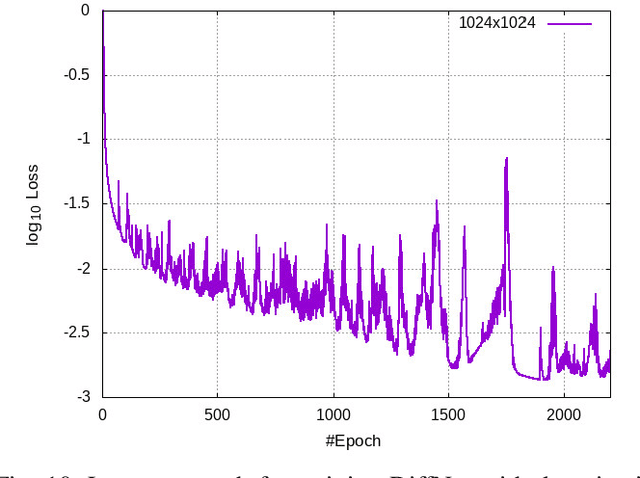
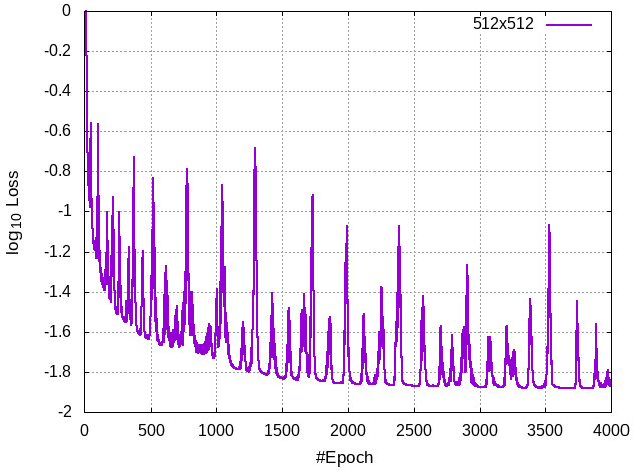
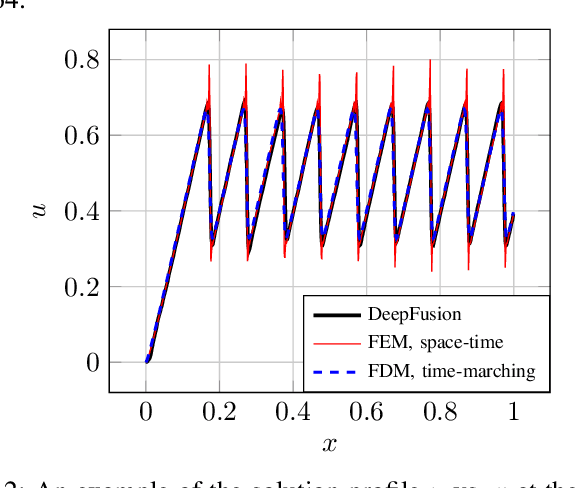
Recent progress in scientific machine learning (SciML) has opened up the possibility of training novel neural network architectures that solve complex partial differential equations (PDEs). Several (nearly data free) approaches have been recently reported that successfully solve PDEs, with examples including deep feed forward networks, generative networks, and deep encoder-decoder networks. However, practical adoption of these approaches is limited by the difficulty in training these models, especially to make predictions at large output resolutions ($\geq 1024 \times 1024$). Here we report on a software framework for data parallel distributed deep learning that resolves the twin challenges of training these large SciML models - training in reasonable time as well as distributing the storage requirements. Our framework provides several out of the box functionality including (a) loss integrity independent of number of processes, (b) synchronized batch normalization, and (c) distributed higher-order optimization methods. We show excellent scalability of this framework on both cloud as well as HPC clusters, and report on the interplay between bandwidth, network topology and bare metal vs cloud. We deploy this approach to train generative models of sizes hitherto not possible, showing that neural PDE solvers can be viably trained for practical applications. We also demonstrate that distributed higher-order optimization methods are $2-3\times$ faster than stochastic gradient-based methods and provide minimal convergence drift with higher batch-size.