Benjamin Recht
Minimax Lower Bounds for $\mathcal{H}_\infty$-Norm Estimation
Sep 28, 2018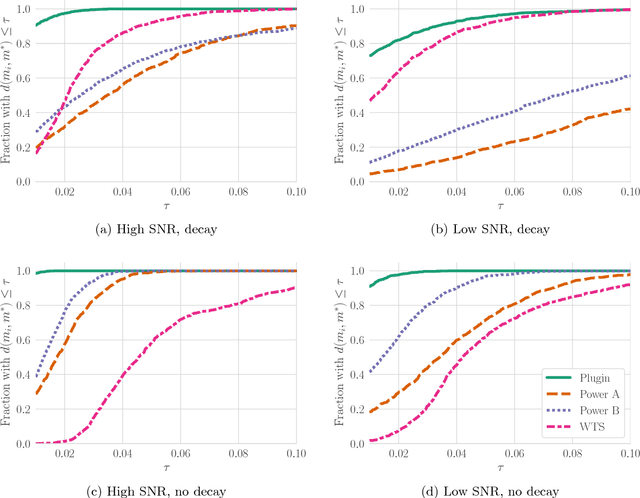
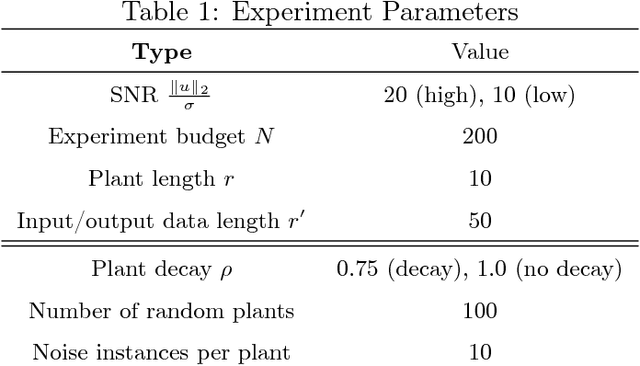
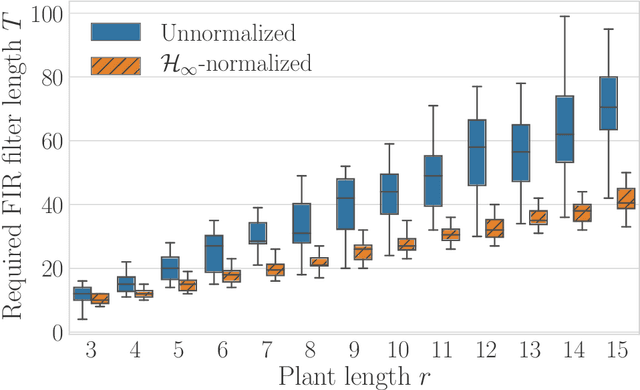
Abstract:The problem of estimating the $\mathcal{H}_\infty$-norm of an LTI system from noisy input/output measurements has attracted recent attention as an alternative to parameter identification for bounding unmodeled dynamics in robust control. In this paper, we study lower bounds for $\mathcal{H}_\infty$-norm estimation under a query model where at each iteration the algorithm chooses a bounded input signal and receives the response of the chosen signal corrupted by white noise. We prove that when the underlying system is an FIR filter, $\mathcal{H}_\infty$-norm estimation is no more efficient than model identification for passive sampling. For active sampling, we show that norm estimation is at most a factor of $\log{r}$ more sample efficient than model identification, where $r$ is the length of the filter. We complement our theoretical results with experiments which demonstrate that a simple non-adaptive estimator of the norm is competitive with state-of-the-art adaptive norm estimation algorithms.
A Successive-Elimination Approach to Adaptive Robotic Sensing
Sep 27, 2018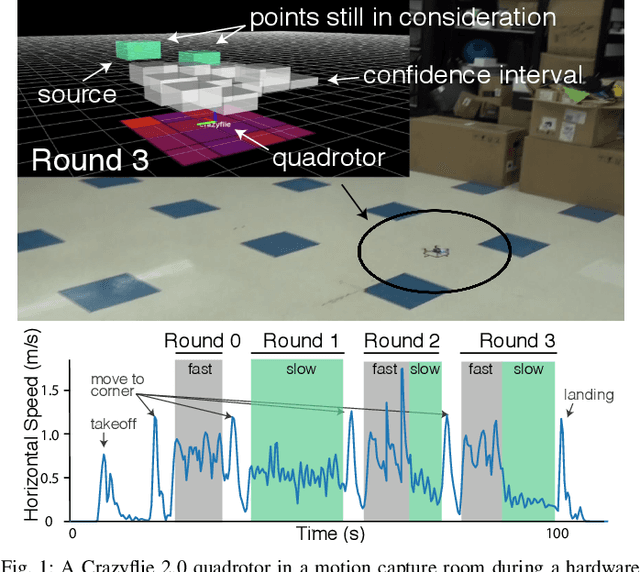
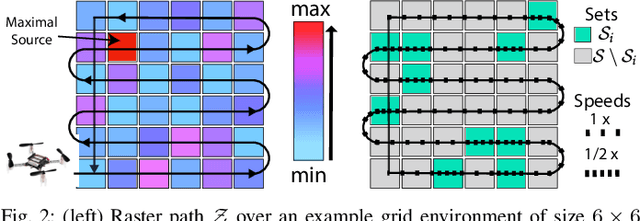
Abstract:We study the adaptive sensing problem for the multiple source seeking problem, where a mobile robot must identify the strongest emitters in an environment with background emissions. Background signals may be highly heterogeneous, and can mislead algorithms which are based on receding horizon control, greedy heuristics, or smooth background priors. We propose AdaSearch, a general algorithm for adaptive sensing. AdaSearch combines global trajectory planning with principled confidence intervals in order to concentrate measurements in promising regions while still guaranteeing sufficient coverage of the entire area. Theoretical analysis shows that AdaSearch significantly outperforms a uniform sampling strategy when the distribution of background signals is highly variable. Simulation studies demonstrate that when applied to the problem of radioactive source-seeking, AdaSearch outperforms both uniform sampling and a receding time horizon information-maximization approach based on the current literature. We corroborate these findings with a hardware demonstration, using a small quadrotor helicopter in a motion-capture arena.
Safely Learning to Control the Constrained Linear Quadratic Regulator
Sep 26, 2018
Abstract:We study the constrained linear quadratic regulator with unknown dynamics, addressing the tension between safety and exploration in data-driven control techniques. We present a framework which allows for system identification through persistent excitation, while maintaining safety by guaranteeing the satisfaction of state and input constraints. This framework involves a novel method for synthesizing robust constraint-satisfying feedback controllers, leveraging newly developed tools from system level synthesis. We connect statistical results with cost sub-optimality bounds to give non-asymptotic guarantees on both estimation and controller performance.
A Tour of Reinforcement Learning: The View from Continuous Control
Jun 25, 2018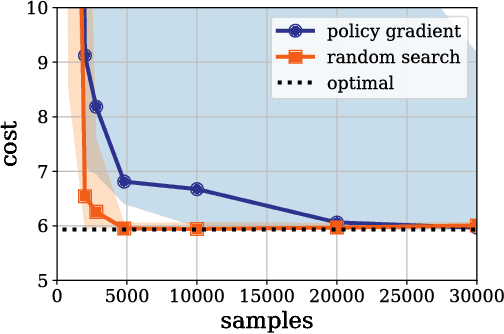
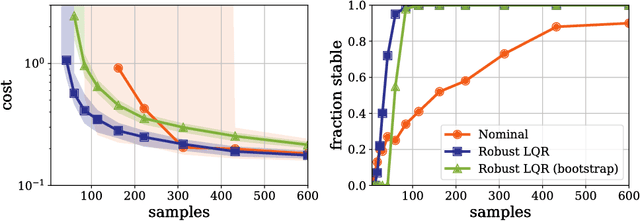
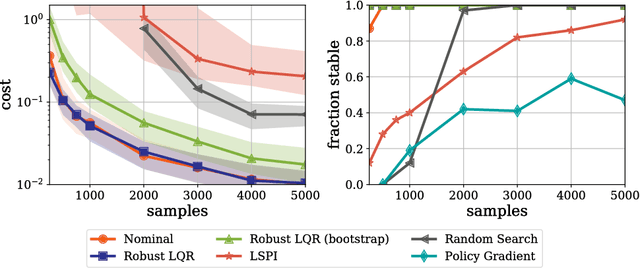
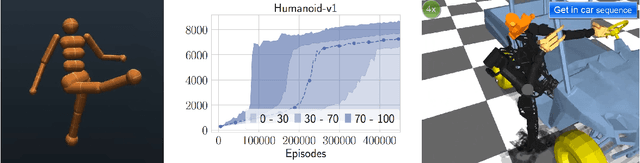
Abstract:This manuscript surveys reinforcement learning from the perspective of optimization and control with a focus on continuous control applications. It surveys the general formulation, terminology, and typical experimental implementations of reinforcement learning and reviews competing solution paradigms. In order to compare the relative merits of various techniques, this survey presents a case study of the Linear Quadratic Regulator (LQR) with unknown dynamics, perhaps the simplest and best studied problem in optimal control. The manuscript describes how merging techniques from learning theory and control can provide non-asymptotic characterizations of LQR performance and shows that these characterizations tend to match experimental behavior. In turn, when revisiting more complex applications, many of the observed phenomena in LQR persist. In particular, theory and experiment demonstrate the role and importance of models and the cost of generality in reinforcement learning algorithms. This survey concludes with a discussion of some of the challenges in designing learning systems that safely and reliably interact with complex and uncertain environments and how tools from reinforcement learning and controls might be combined to approach these challenges.
Do CIFAR-10 Classifiers Generalize to CIFAR-10?
Jun 01, 2018
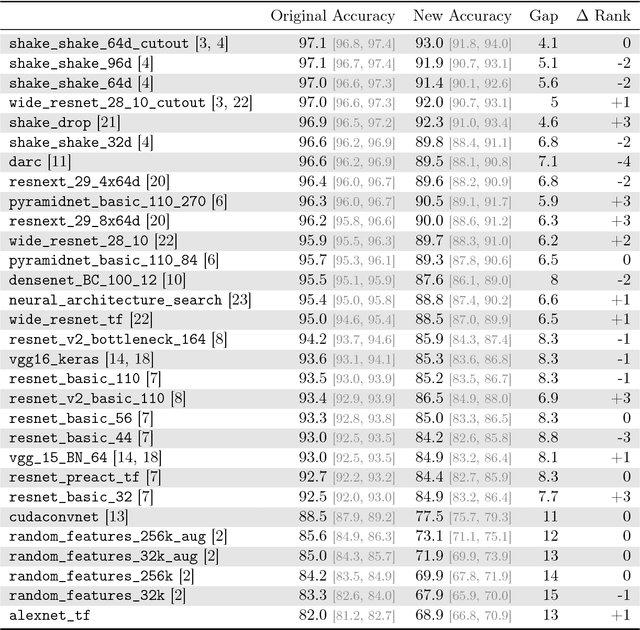
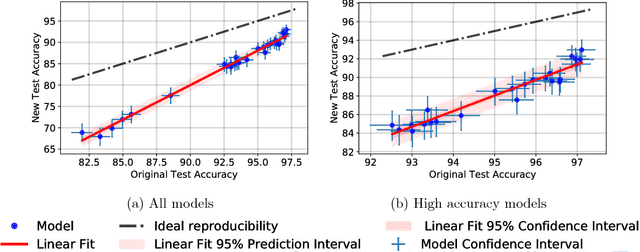

Abstract:Machine learning is currently dominated by largely experimental work focused on improvements in a few key tasks. However, the impressive accuracy numbers of the best performing models are questionable because the same test sets have been used to select these models for multiple years now. To understand the danger of overfitting, we measure the accuracy of CIFAR-10 classifiers by creating a new test set of truly unseen images. Although we ensure that the new test set is as close to the original data distribution as possible, we find a large drop in accuracy (4% to 10%) for a broad range of deep learning models. Yet more recent models with higher original accuracy show a smaller drop and better overall performance, indicating that this drop is likely not due to overfitting based on adaptivity. Instead, we view our results as evidence that current accuracy numbers are brittle and susceptible to even minute natural variations in the data distribution.
Learning Without Mixing: Towards A Sharp Analysis of Linear System Identification
May 24, 2018Abstract:We prove that the ordinary least-squares (OLS) estimator attains nearly minimax optimal performance for the identification of linear dynamical systems from a single observed trajectory. Our upper bound relies on a generalization of Mendelson's small-ball method to dependent data, eschewing the use of standard mixing-time arguments. Our lower bounds reveal that these upper bounds match up to logarithmic factors. In particular, we capture the correct signal-to-noise behavior of the problem, showing that more unstable linear systems are easier to estimate. This behavior is qualitatively different from arguments which rely on mixing-time calculations that suggest that unstable systems are more difficult to estimate. We generalize our technique to provide bounds for a more general class of linear response time-series.
Regret Bounds for Robust Adaptive Control of the Linear Quadratic Regulator
May 23, 2018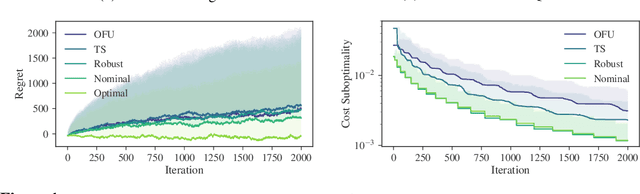
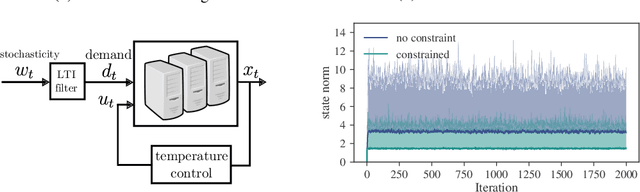
Abstract:We consider adaptive control of the Linear Quadratic Regulator (LQR), where an unknown linear system is controlled subject to quadratic costs. Leveraging recent developments in the estimation of linear systems and in robust controller synthesis, we present the first provably polynomial time algorithm that provides high probability guarantees of sub-linear regret on this problem. We further study the interplay between regret minimization and parameter estimation by proving a lower bound on the expected regret in terms of the exploration schedule used by any algorithm. Finally, we conduct a numerical study comparing our robust adaptive algorithm to other methods from the adaptive LQR literature, and demonstrate the flexibility of our proposed method by extending it to a demand forecasting problem subject to state constraints.
The Marginal Value of Adaptive Gradient Methods in Machine Learning
May 22, 2018
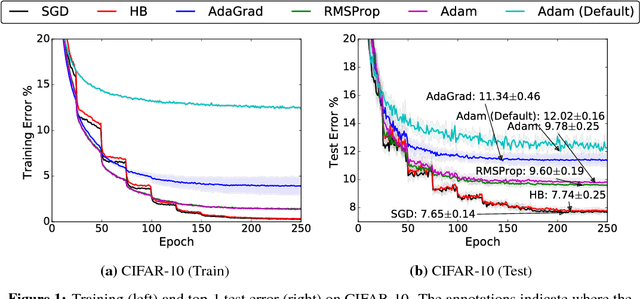

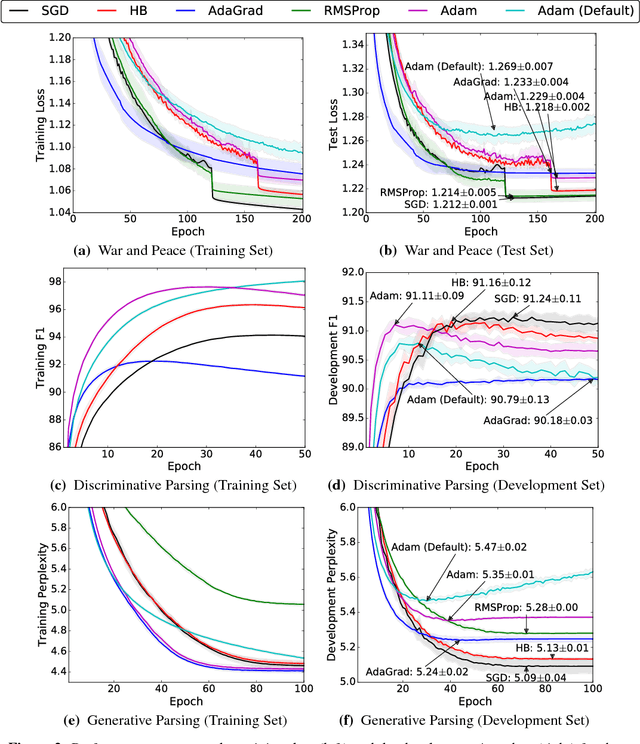
Abstract:Adaptive optimization methods, which perform local optimization with a metric constructed from the history of iterates, are becoming increasingly popular for training deep neural networks. Examples include AdaGrad, RMSProp, and Adam. We show that for simple overparameterized problems, adaptive methods often find drastically different solutions than gradient descent (GD) or stochastic gradient descent (SGD). We construct an illustrative binary classification problem where the data is linearly separable, GD and SGD achieve zero test error, and AdaGrad, Adam, and RMSProp attain test errors arbitrarily close to half. We additionally study the empirical generalization capability of adaptive methods on several state-of-the-art deep learning models. We observe that the solutions found by adaptive methods generalize worse (often significantly worse) than SGD, even when these solutions have better training performance. These results suggest that practitioners should reconsider the use of adaptive methods to train neural networks.
Tight Query Complexity Lower Bounds for PCA via Finite Sample Deformed Wigner Law
Apr 04, 2018Abstract:We prove a \emph{query complexity} lower bound for approximating the top $r$ dimensional eigenspace of a matrix. We consider an oracle model where, given a symmetric matrix $\mathbf{M} \in \mathbb{R}^{d \times d}$, an algorithm $\mathsf{Alg}$ is allowed to make $\mathsf{T}$ exact queries of the form $\mathsf{w}^{(i)} = \mathbf{M} \mathsf{v}^{(i)}$ for $i$ in $\{1,...,\mathsf{T}\}$, where $\mathsf{v}^{(i)}$ is drawn from a distribution which depends arbitrarily on the past queries and measurements $\{\mathsf{v}^{(j)},\mathsf{w}^{(i)}\}_{1 \le j \le i-1}$. We show that for every $\mathtt{gap} \in (0,1/2]$, there exists a distribution over matrices $\mathbf{M}$ for which 1) $\mathrm{gap}_r(\mathbf{M}) = \Omega(\mathtt{gap})$ (where $\mathrm{gap}_r(\mathbf{M})$ is the normalized gap between the $r$ and $r+1$-st largest-magnitude eigenvector of $\mathbf{M}$), and 2) any algorithm $\mathsf{Alg}$ which takes fewer than $\mathrm{const} \times \frac{r \log d}{\sqrt{\mathtt{gap}}}$ queries fails (with overwhelming probability) to identity a matrix $\widehat{\mathsf{V}} \in \mathbb{R}^{d \times r}$ with orthonormal columns for which $\langle \widehat{\mathsf{V}}, \mathbf{M} \widehat{\mathsf{V}}\rangle \ge (1 - \mathrm{const} \times \mathtt{gap})\sum_{i=1}^r \lambda_i(\mathbf{M})$. Our bound requires only that $d$ is a small polynomial in $1/\mathtt{gap}$ and $r$, and matches the upper bounds of Musco and Musco '15. Moreover, it establishes a strict separation between convex optimization and \emph{randomized}, "strict-saddle" non-convex optimization of which PCA is a canonical example: in the former, first-order methods can have dimension-free iteration complexity, whereas in PCA, the iteration complexity of gradient-based methods must necessarily grow with the dimension.
Finite-Data Performance Guarantees for the Output-Feedback Control of an Unknown System
Mar 25, 2018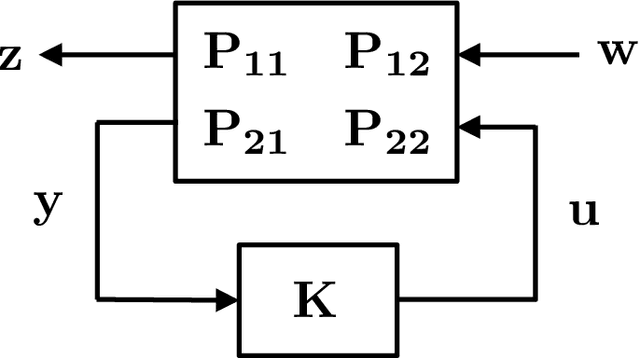
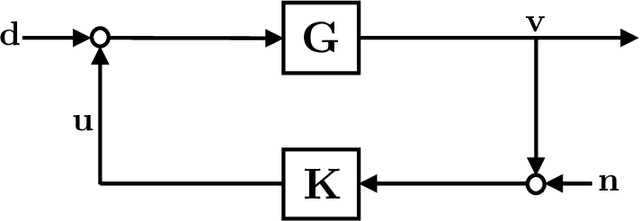
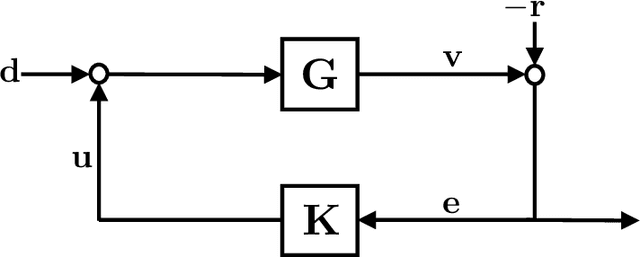
Abstract:As the systems we control become more complex, first-principle modeling becomes either impossible or intractable, motivating the use of machine learning techniques for the control of systems with continuous action spaces. As impressive as the empirical success of these methods have been, strong theoretical guarantees of performance, safety, or robustness are few and far between. This paper takes a step towards such providing such guarantees by establishing finite-data performance guarantees for the robust output-feedback control of an unknown FIR SISO system. In particular, we introduce the "Coarse-ID control" pipeline, which is composed of a system identification step followed by a robust controller synthesis procedure, and analyze its end-to-end performance, providing quantitative bounds on the performance degradation suffered due to model uncertainty as a function of the number of experiments run to identify the system. We conclude with numerical examples demonstrating the effectiveness of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge