Robust Guarantees for Perception-Based Control

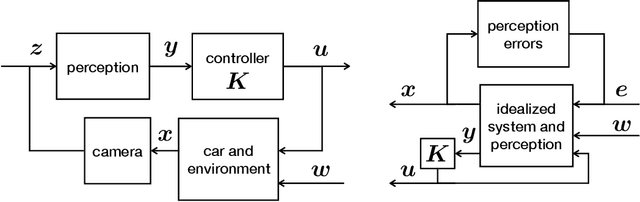
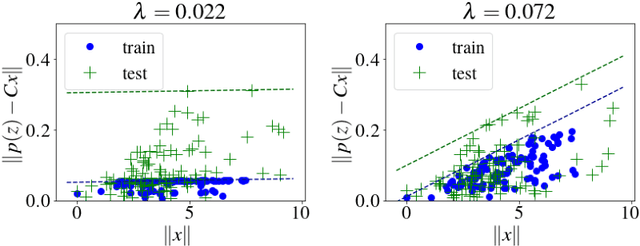
Motivated by vision based control of autonomous vehicles, we consider the problem of controlling a known linear dynamical system for which partial state information, such as vehicle position, can only be extracted from high-dimensional data, such as an image. Our approach is to learn a perception map from high-dimensional data to partial-state observation and its corresponding error profile, and then design a robust controller. We show that under suitable smoothness assumptions on the perception map and generative model relating state to high-dimensional data, an affine error model is sufficiently rich to capture all possible error profiles, and can further be learned via a robust regression problem. We then show how to integrate the learned perception map and error model into a novel robust control synthesis procedure, and prove that the resulting perception and control loop has favorable generalization properties. Finally, we illustrate the usefulness of our approach on a synthetic example and on the self-driving car simulation platform CARLA.

A systematic framework for natural perturbations from videos

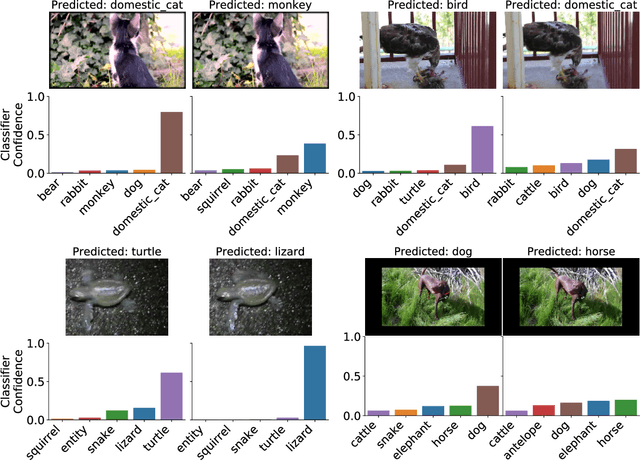
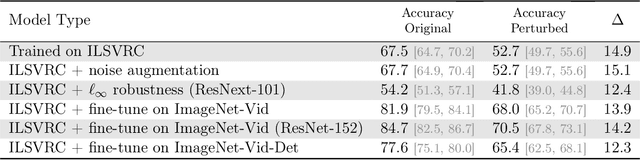
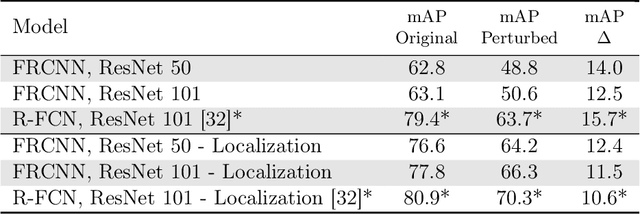
We introduce a systematic framework for quantifying the robustness of classifiers to naturally occurring perturbations of images found in videos. As part of this framework, we construct Imagenet-Video-Robust, a human-expert--reviewed dataset of 22,178 images grouped into 1,109 sets of perceptually similar images derived from frames in the ImageNet Video Object Detection dataset. We evaluate a diverse array of classifiers trained on ImageNet, including models trained for robustness, and show a median classification accuracy drop of 16%. Additionally, we evaluate the Faster R-CNN and R-FCN models for detection, and show that natural perturbations induce both classification as well as localization errors, leading to a median drop in detection mAP of 14 points. Our analysis shows that natural perturbations in the real world are heavily problematic for current CNNs, posing a significant challenge to their deployment in safety-critical environments that require reliable, low-latency predictions.

Finite-time Analysis of Approximate Policy Iteration for the Linear Quadratic Regulator

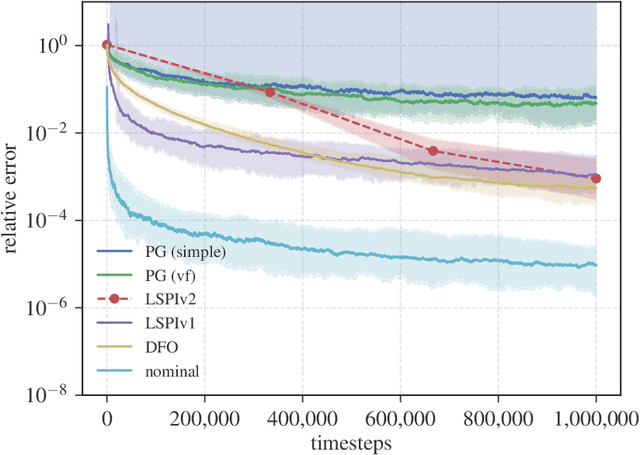
We study the sample complexity of approximate policy iteration (PI) for the Linear Quadratic Regulator (LQR), building on a recent line of work using LQR as a testbed to understand the limits of reinforcement learning (RL) algorithms on continuous control tasks. Our analysis quantifies the tension between policy improvement and policy evaluation, and suggests that policy evaluation is the dominant factor in terms of sample complexity. Specifically, we show that to obtain a controller that is within $\varepsilon$ of the optimal LQR controller, each step of policy evaluation requires at most $(n+d)^3/\varepsilon^2$ samples, where $n$ is the dimension of the state vector and $d$ is the dimension of the input vector. On the other hand, only $\log(1/\varepsilon)$ policy improvement steps suffice, resulting in an overall sample complexity of $(n+d)^3 \varepsilon^{-2} \log(1/\varepsilon)$. We furthermore build on our analysis and construct a simple adaptive procedure based on $\varepsilon$-greedy exploration which relies on approximate PI as a sub-routine and obtains $T^{2/3}$ regret, improving upon a recent result of Abbasi-Yadkori et al.

Model Similarity Mitigates Test Set Overuse

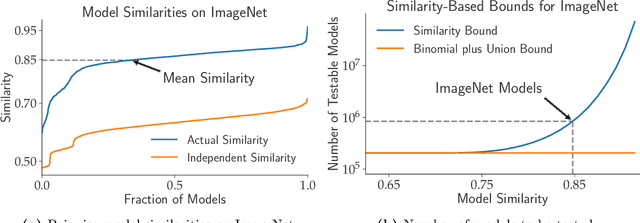
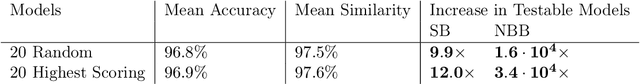
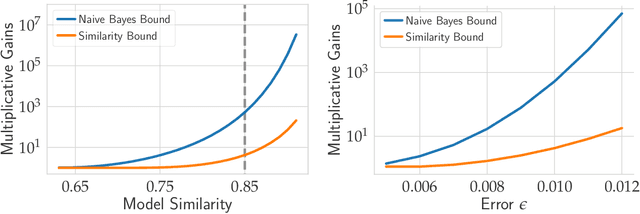
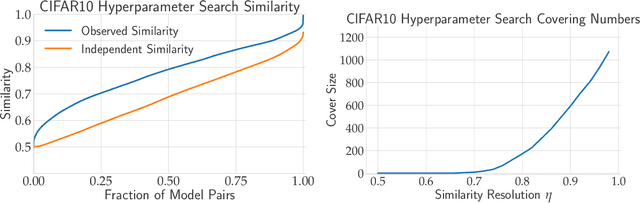
Excessive reuse of test data has become commonplace in today's machine learning workflows. Popular benchmarks, competitions, industrial scale tuning, among other applications, all involve test data reuse beyond guidance by statistical confidence bounds. Nonetheless, recent replication studies give evidence that popular benchmarks continue to support progress despite years of extensive reuse. We proffer a new explanation for the apparent longevity of test data: Many proposed models are similar in their predictions and we prove that this similarity mitigates overfitting. Specifically, we show empirically that models proposed for the ImageNet ILSVRC benchmark agree in their predictions well beyond what we can conclude from their accuracy levels alone. Likewise, models created by large scale hyperparameter search enjoy high levels of similarity. Motivated by these empirical observations, we give a non-asymptotic generalization bound that takes similarity into account, leading to meaningful confidence bounds in practical settings.

Certainty Equivalent Control of LQR is Efficient

We study the performance of the certainty equivalent controller on the Linear Quadratic Regulator (LQR) with unknown transition dynamics. We show that the sub-optimality gap between the cost incurred by playing the certainty equivalent controller on the true system and the cost incurred by using the optimal LQR controller enjoys a fast statistical rate, scaling as the square of the parameter error. Our result improves upon recent work by Dean et al. (2017), who present an algorithm achieving a sub-optimality gap linear in the parameter error. A key part of our analysis relies on perturbation bounds for discrete Riccati equations. We provide two new perturbation bounds, one that expands on an existing result from Konstantinov et al. (1993), and another based on a new elementary proof strategy. Our results show that certainty equivalent control with $\varepsilon$-greedy exploration achieves $\tilde{\mathcal{O}}(\sqrt{T})$ regret in the adaptive LQR setting, yielding the first guarantee of a computationally tractable algorithm that achieves nearly optimal regret for adaptive LQR.

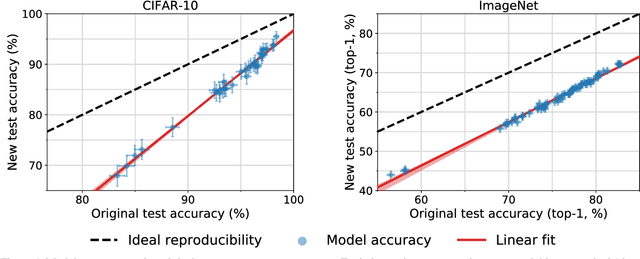
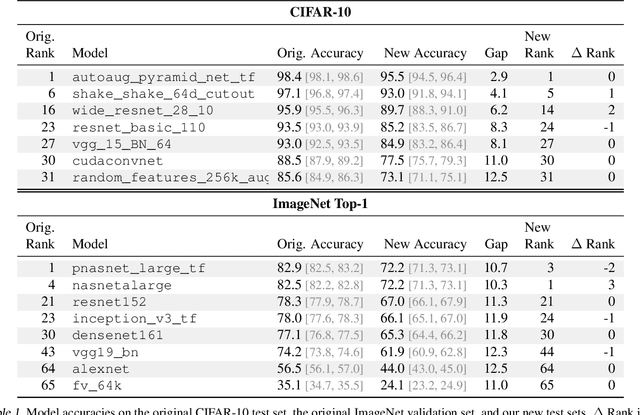
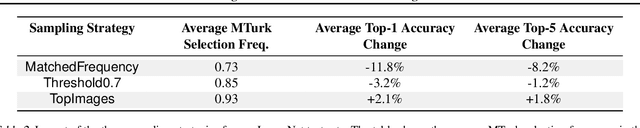
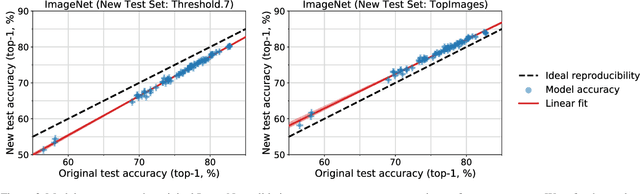
Do ImageNet Classifiers Generalize to ImageNet?

We build new test sets for the CIFAR-10 and ImageNet datasets. Both benchmarks have been the focus of intense research for almost a decade, raising the danger of overfitting to excessively re-used test sets. By closely following the original dataset creation processes, we test to what extent current classification models generalize to new data. We evaluate a broad range of models and find accuracy drops of 3% - 15% on CIFAR-10 and 11% - 14% on ImageNet. However, accuracy gains on the original test sets translate to larger gains on the new test sets. Our results suggest that the accuracy drops are not caused by adaptivity, but by the models' inability to generalize to slightly "harder" images than those found in the original test sets.

Learning Linear Dynamical Systems with Semi-Parametric Least Squares

We analyze a simple prefiltered variation of the least squares estimator for the problem of estimation with biased, semi-parametric noise, an error model studied more broadly in causal statistics and active learning. We prove an oracle inequality which demonstrates that this procedure provably mitigates the variance introduced by long-term dependencies. We then demonstrate that prefiltered least squares yields, to our knowledge, the first algorithm that provably estimates the parameters of partially-observed linear systems that attains rates which do not not incur a worst-case dependence on the rate at which these dependencies decay. The algorithm is provably consistent even for systems which satisfy the weaker marginal stability condition obeyed by many classical models based on Newtonian mechanics. In this context, our semi-parametric framework yields guarantees for both stochastic and worst-case noise.

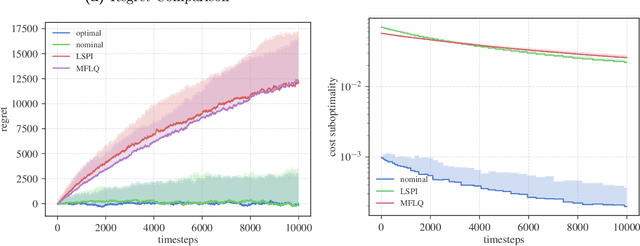
The Gap Between Model-Based and Model-Free Methods on the Linear Quadratic Regulator: An Asymptotic Viewpoint

The effectiveness of model-based versus model-free methods is a long-standing question in reinforcement learning (RL). Motivated by recent empirical success of RL on continuous control tasks, we study the sample complexity of popular model-based and model-free algorithms on the Linear Quadratic Regulator (LQR). We show that for policy evaluation, a simple model-based plugin method requires asymptotically less samples than the classical least-squares temporal difference (LSTD) estimator to reach the same quality of solution; the sample complexity gap between the two methods can be at least a factor of state dimension. For policy evaluation, we study a simple family of problem instances and show that nominal (certainty equivalence principle) control also requires a factor of state dimension fewer samples than the policy gradient method to reach the same level of control performance on these instances. Furthermore, the gap persists even when employing baselines commonly used in practice. To the best of our knowledge, this is the first theoretical result which demonstrates a separation in the sample complexity between model-based and model-free methods on a continuous control task.

Massively Parallel Hyperparameter Tuning

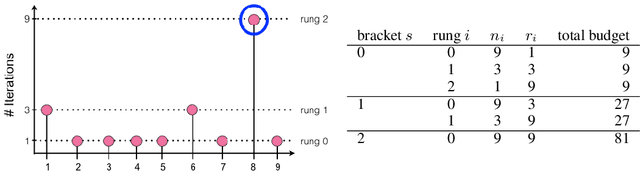
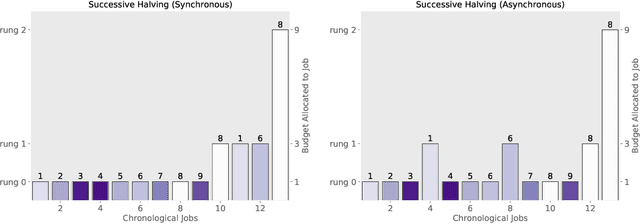
Modern learning models are characterized by large hyperparameter spaces. In order to adequately explore these large spaces, we must evaluate a large number of configurations, typically orders of magnitude more configurations than available parallel workers. Given the growing costs of model training, we would ideally like to perform this search in roughly the same wall-clock time needed to train a single model. In this work, we tackle this challenge by introducing ASHA, a simple and robust hyperparameter tuning algorithm with solid theoretical underpinnings that exploits parallelism and aggressive early-stopping. Our extensive empirical results show that ASHA slightly outperforms Fabolas and Population Based Tuning, state-of-the hyperparameter tuning methods; scales linearly with the number of workers in distributed settings; converges to a high quality configuration in half the time taken by Vizier (Google's internal hyperparameter tuning service) in an experiment with 500 workers; and beats the published result for a near state-of-the-art LSTM architecture in under 2x the time to train a single model.

Minimax Lower Bounds for $\mathcal{H}_\infty$-Norm Estimation

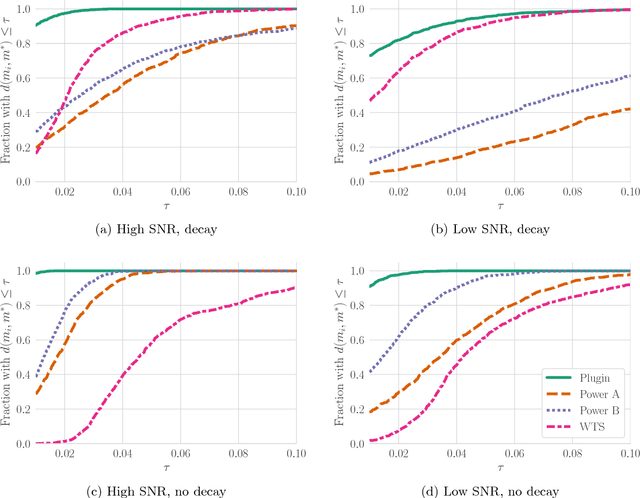
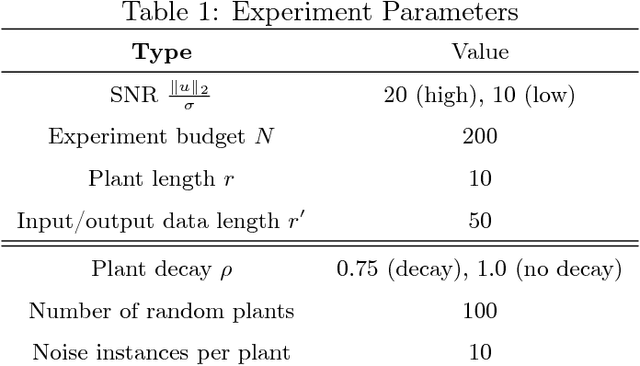
The problem of estimating the $\mathcal{H}_\infty$-norm of an LTI system from noisy input/output measurements has attracted recent attention as an alternative to parameter identification for bounding unmodeled dynamics in robust control. In this paper, we study lower bounds for $\mathcal{H}_\infty$-norm estimation under a query model where at each iteration the algorithm chooses a bounded input signal and receives the response of the chosen signal corrupted by white noise. We prove that when the underlying system is an FIR filter, $\mathcal{H}_\infty$-norm estimation is no more efficient than model identification for passive sampling. For active sampling, we show that norm estimation is at most a factor of $\log{r}$ more sample efficient than model identification, where $r$ is the length of the filter. We complement our theoretical results with experiments which demonstrate that a simple non-adaptive estimator of the norm is competitive with state-of-the-art adaptive norm estimation algorithms.