Universal Exact Compression of Differentially Private Mechanisms

To reduce the communication cost of differential privacy mechanisms, we introduce a novel construction, called Poisson private representation (PPR), designed to compress and simulate any local randomizer while ensuring local differential privacy. Unlike previous simulation-based local differential privacy mechanisms, PPR exactly preserves the joint distribution of the data and the output of the original local randomizer. Hence, the PPR-compressed privacy mechanism retains all desirable statistical properties of the original privacy mechanism such as unbiasedness and Gaussianity. Moreover, PPR achieves a compression size within a logarithmic gap from the theoretical lower bound. Using the PPR, we give a new order-wise trade-off between communication, accuracy, central and local differential privacy for distributed mean estimation. Experiment results on distributed mean estimation show that PPR consistently gives a better trade-off between communication, accuracy and central differential privacy compared to the coordinate subsampled Gaussian mechanism, while also providing local differential privacy.

Differentially Private Decoupled Graph Convolutions for Multigranular Topology Protection

Graph learning methods, such as Graph Neural Networks (GNNs) based on graph convolutions, are highly successful in solving real-world learning problems involving graph-structured data. However, graph learning methods expose sensitive user information and interactions not only through their model parameters but also through their model predictions. Consequently, standard Differential Privacy (DP) techniques that merely offer model weight privacy are inadequate. This is especially the case for node predictions that leverage neighboring node attributes directly via graph convolutions that create additional risks of privacy leakage. To address this problem, we introduce Graph Differential Privacy (GDP), a new formal DP framework tailored to graph learning settings that ensures both provably private model parameters and predictions. Furthermore, since there may be different privacy requirements for the node attributes and graph structure, we introduce a novel notion of relaxed node-level data adjacency. This relaxation can be used for establishing guarantees for different degrees of graph topology privacy while maintaining node attribute privacy. Importantly, this relaxation reveals a useful trade-off between utility and topology privacy for graph learning methods. In addition, our analysis of GDP reveals that existing DP-GNNs fail to exploit this trade-off due to the complex interplay between graph topology and attribute data in standard graph convolution designs. To mitigate this problem, we introduce the Differentially Private Decoupled Graph Convolution (DPDGC) model, which benefits from decoupled graph convolution while providing GDP guarantees. Extensive experiments on seven node classification benchmarking datasets demonstrate the superior privacy-utility trade-off of DPDGC over existing DP-GNNs based on standard graph convolution design.

Training generative models from privatized data

Local differential privacy (LDP) is a powerful method for privacy-preserving data collection. In this paper, we develop a framework for training Generative Adversarial Networks (GAN) on differentially privatized data. We show that entropic regularization of the Wasserstein distance -- a popular regularization method in the literature that has been often leveraged for its computational benefits -- can be used to denoise the data distribution when data is privatized by common additive noise mechanisms, such as Laplace and Gaussian. This combination uniquely enables the mitigation of both the regularization bias and the effects of privatization noise, thereby enhancing the overall efficacy of the model. We analyse the proposed method, provide sample complexity results and experimental evidence to support its efficacy.

Breaking The Dimension Dependence in Sparse Distribution Estimation under Communication Constraints

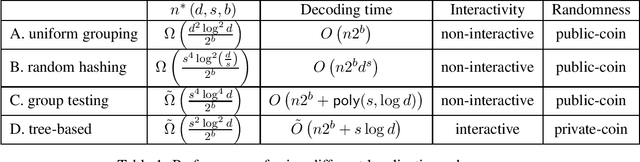
We consider the problem of estimating a $d$-dimensional $s$-sparse discrete distribution from its samples observed under a $b$-bit communication constraint. The best-known previous result on $\ell_2$ estimation error for this problem is $O\left( \frac{s\log\left( {d}/{s}\right)}{n2^b}\right)$. Surprisingly, we show that when sample size $n$ exceeds a minimum threshold $n^*(s, d, b)$, we can achieve an $\ell_2$ estimation error of $O\left( \frac{s}{n2^b}\right)$. This implies that when $n>n^*(s, d, b)$ the convergence rate does not depend on the ambient dimension $d$ and is the same as knowing the support of the distribution beforehand. We next ask the question: ``what is the minimum $n^*(s, d, b)$ that allows dimension-free convergence?''. To upper bound $n^*(s, d, b)$, we develop novel localization schemes to accurately and efficiently localize the unknown support. For the non-interactive setting, we show that $n^*(s, d, b) = O\left( \min \left( {d^2\log^2 d}/{2^b}, {s^4\log^2 d}/{2^b}\right) \right)$. Moreover, we connect the problem with non-adaptive group testing and obtain a polynomial-time estimation scheme when $n = \tilde{\Omega}\left({s^4\log^4 d}/{2^b}\right)$. This group testing based scheme is adaptive to the sparsity parameter $s$, and hence can be applied without knowing it. For the interactive setting, we propose a novel tree-based estimation scheme and show that the minimum sample-size needed to achieve dimension-free convergence can be further reduced to $n^*(s, d, b) = \tilde{O}\left( {s^2\log^2 d}/{2^b} \right)$.

Breaking the Communication-Privacy-Accuracy Trilemma

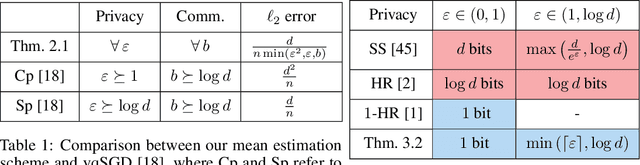
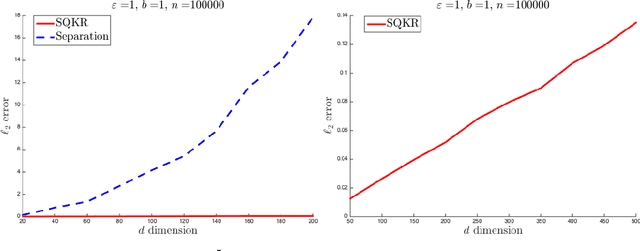
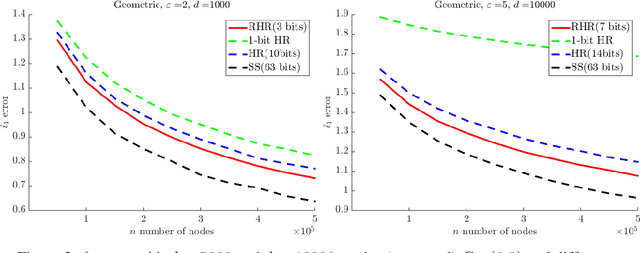
Two major challenges in distributed learning and estimation are 1) preserving the privacy of the local samples; and 2) communicating them efficiently to a central server, while achieving high accuracy for the end-to-end task. While there has been significant interest in addressing each of these challenges separately in the recent literature, treatments that simultaneously address both challenges are still largely missing. In this paper, we develop novel encoding and decoding mechanisms that simultaneously achieve optimal privacy and communication efficiency in various canonical settings. In particular, we consider the problems of mean estimation and frequency estimation under $\varepsilon$-local differential privacy and $b$-bit communication constraints. For mean estimation, we propose a scheme based on Kashin's representation and random sampling, with order-optimal estimation error under both constraints. For frequency estimation, we present a mechanism that leverages the recursive structure of Walsh-Hadamard matrices and achieves order-optimal estimation error for all privacy levels and communication budgets. As a by-product, we also construct a distribution estimation mechanism that is rate-optimal for all privacy regimes and communication constraints, extending recent work that is limited to $b=1$ and $\varepsilon=O(1)$. Our results demonstrate that intelligent encoding under joint privacy and communication constraints can yield a performance that matches the optimal accuracy achievable under either constraint alone.

Lower Bounds and a Near-Optimal Shrinkage Estimator for Least Squares using Random Projections

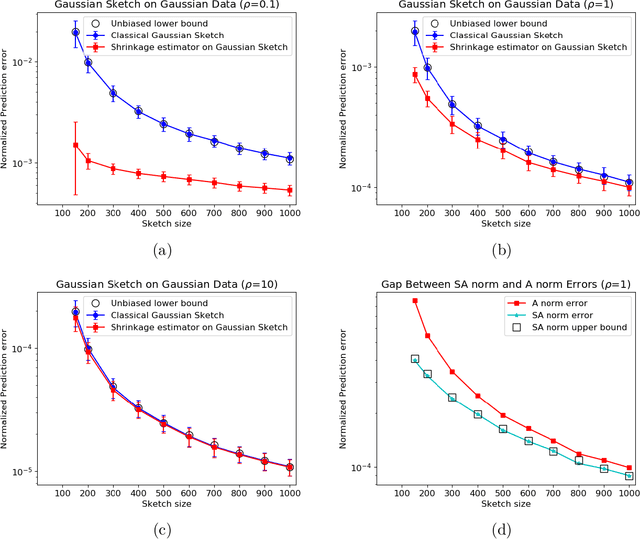
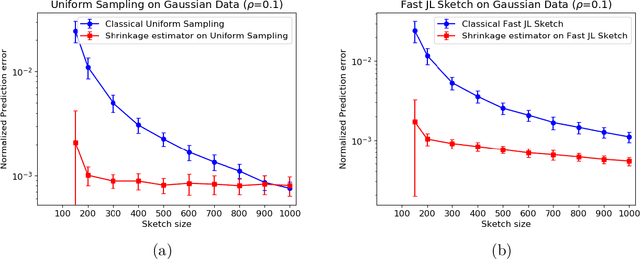
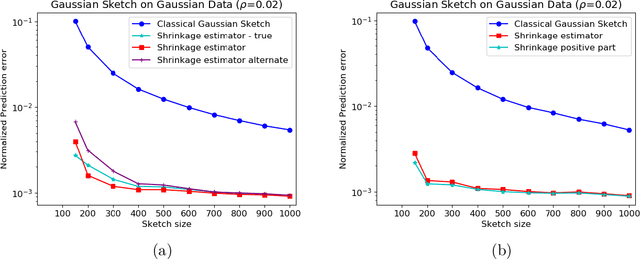
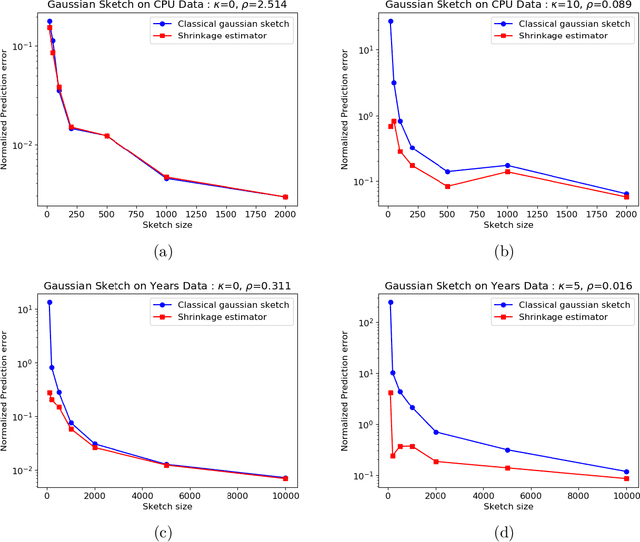
In this work, we consider the deterministic optimization using random projections as a statistical estimation problem, where the squared distance between the predictions from the estimator and the true solution is the error metric. In approximately solving a large scale least squares problem using Gaussian sketches, we show that the sketched solution has a conditional Gaussian distribution with the true solution as its mean. Firstly, tight worst case error lower bounds with explicit constants are derived for any estimator using the Gaussian sketch, and the classical sketching is shown to be the optimal unbiased estimator. For biased estimators, the lower bound also incorporates prior knowledge about the true solution. Secondly, we use the James-Stein estimator to derive an improved estimator for the least squares solution using the Gaussian sketch. An upper bound on the expected error of this estimator is derived, which is smaller than the error of the classical Gaussian sketch solution for any given data. The upper and lower bounds match when the SNR of the true solution is known to be small and the data matrix is well conditioned. Empirically, this estimator achieves smaller error on simulated and real datasets, and works for other common sketching methods as well.

Advances and Open Problems in Federated Learning

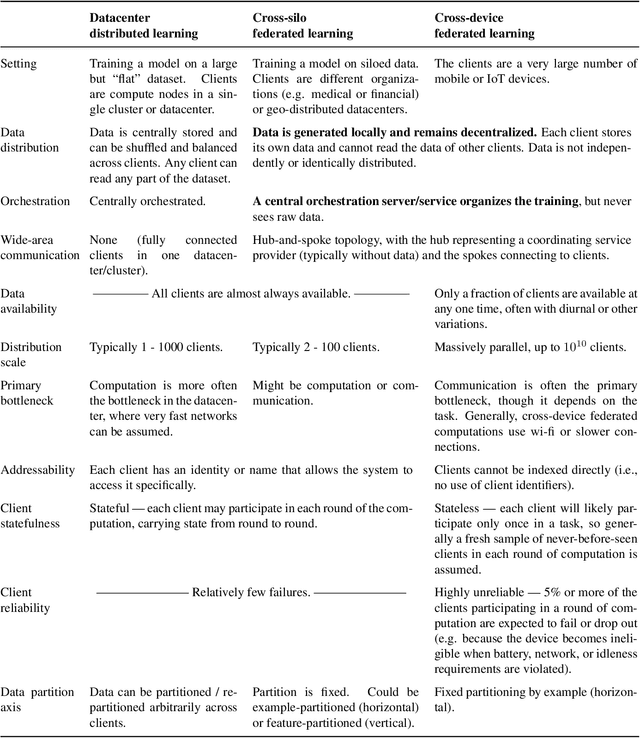
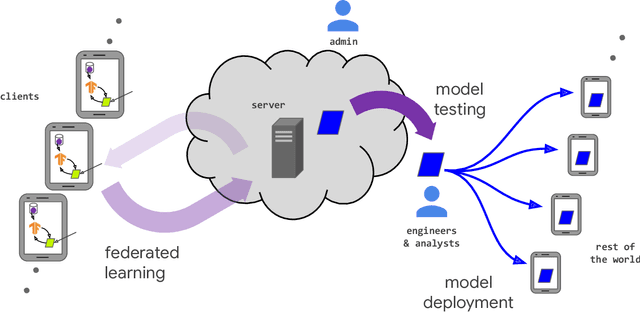
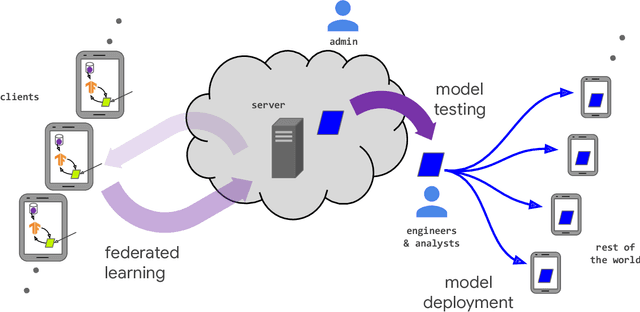
Federated learning (FL) is a machine learning setting where many clients (e.g. mobile devices or whole organizations) collaboratively train a model under the orchestration of a central server (e.g. service provider), while keeping the training data decentralized. FL embodies the principles of focused data collection and minimization, and can mitigate many of the systemic privacy risks and costs resulting from traditional, centralized machine learning and data science approaches. Motivated by the explosive growth in FL research, this paper discusses recent advances and presents an extensive collection of open problems and challenges.

Phase Retrieval via Incremental Truncated Wirtinger Flow

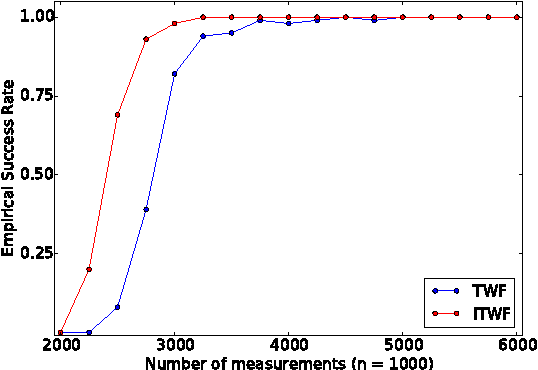
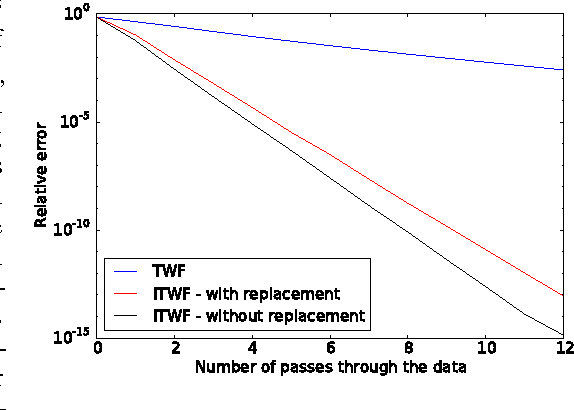
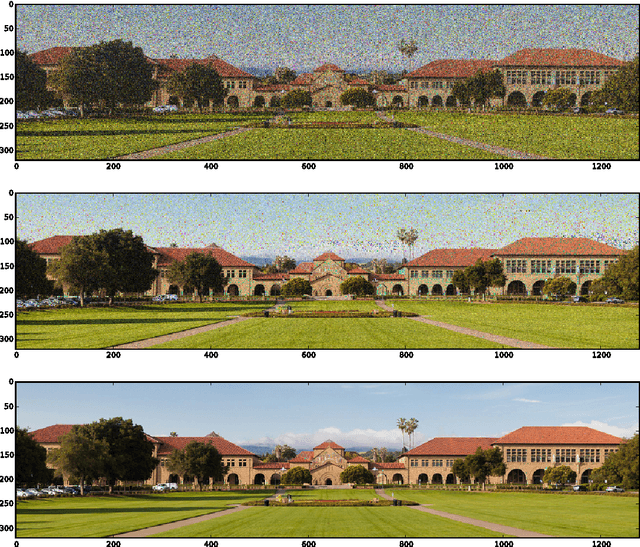
In the phase retrieval problem, an unknown vector is to be recovered given quadratic measurements. This problem has received considerable attention in recent times. In this paper, we present an algorithm to solve a nonconvex formulation of the phase retrieval problem, that we call $\textit{Incremental Truncated Wirtinger Flow}$. Given random Gaussian sensing vectors, we prove that it converges linearly to the solution, with an optimal sample complexity. We also provide stability guarantees of the algorithm under noisy measurements. Performance and comparisons with existing algorithms are illustrated via numerical experiments on simulated and real data, with both random and structured sensing vectors.