Variational Inference with Continuously-Indexed Normalizing Flows

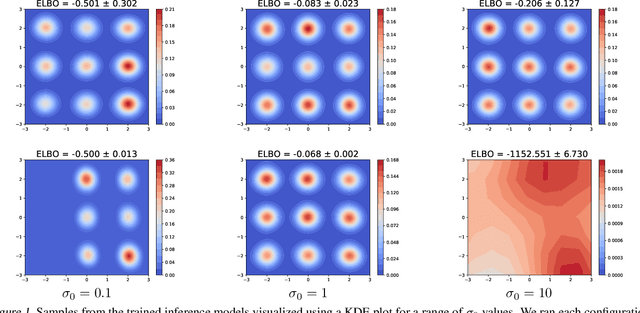
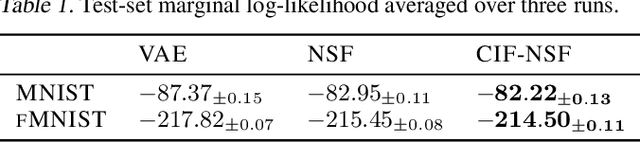
Continuously-indexed flows (CIFs) have recently achieved improvements over baseline normalizing flows in a variety of density estimation tasks. In this paper, we adapt CIFs to the task of variational inference (VI) through the framework of auxiliary VI, and demonstrate that the advantages of CIFs over baseline flows can also translate to the VI setting for both sampling from posteriors with complicated topology and performing maximum likelihood estimation in latent-variable models.

Pruning untrained neural networks: Principles and Analysis

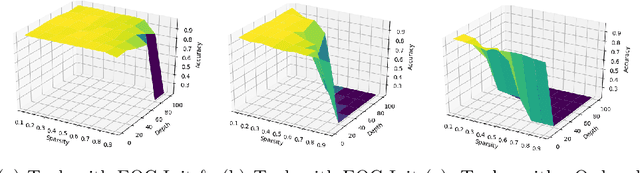
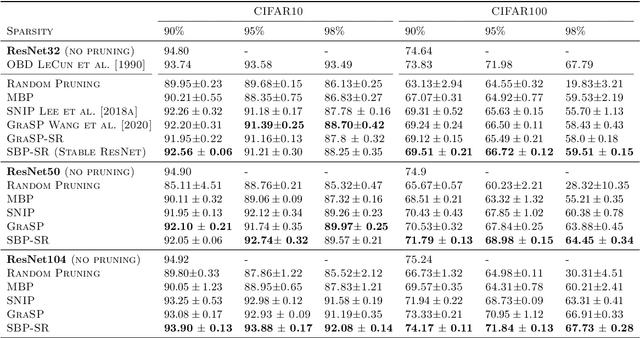
Overparameterized neural networks display state-of-the art performance. However, there is a growing need for smaller, energy-efficient, neural networks to be able to use machine learning applications on devices with limited computational resources. A popular approach consists of using pruning techniques. While these techniques have traditionally focused on pruning pre-trained neural networks (e.g. LeCun et al. (1990) and Hassabi et al. (1993)), recent work by Lee et al. (2018) showed promising results where pruning is performed at initialization. However, such procedures remain unsatisfactory as the resulting pruned networks can be difficult to train and, for instance, these procedures do not prevent one layer being fully pruned. In this paper we provide a comprehensive theoretical analysis of pruning at initialization and training sparse architectures. This analysis allows us to propose novel principled approaches which we validate experimentally on a variety of network architectures. We particularly show that we can prune up to 99.9% of the weights while keeping the model trainable.

Schrödinger Bridge Samplers

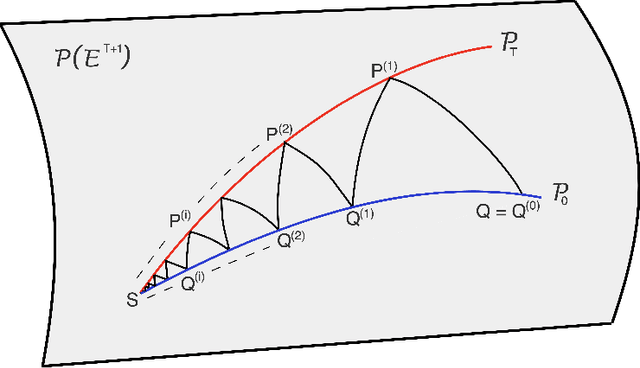
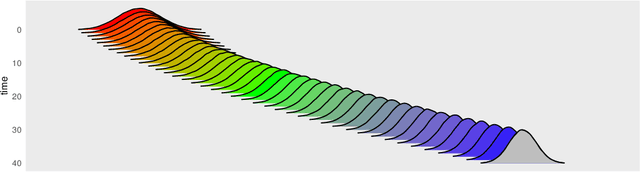
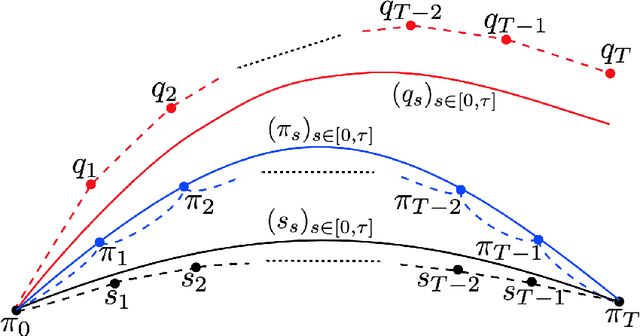
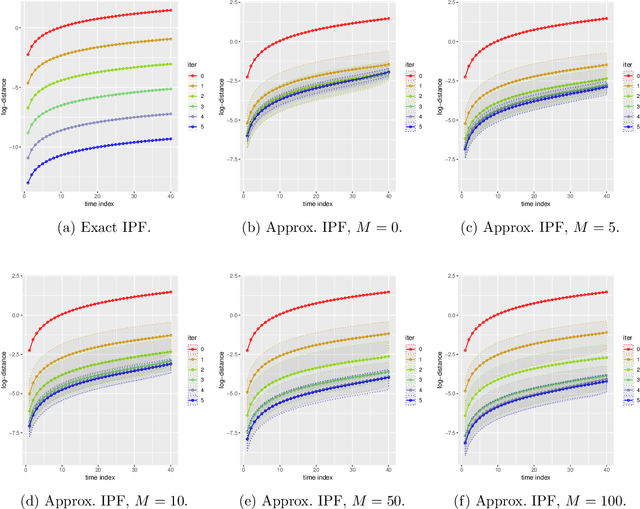
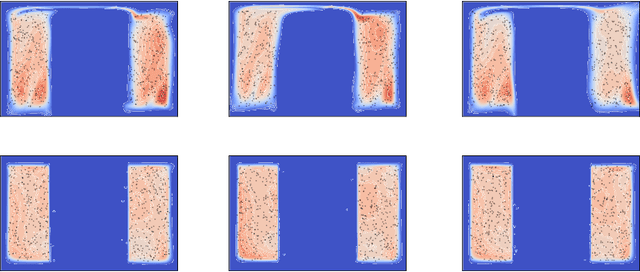
Consider a reference Markov process with initial distribution $\pi_{0}$ and transition kernels $\{M_{t}\}_{t\in[1:T]}$, for some $T\in\mathbb{N}$. Assume that you are given distribution $\pi_{T}$, which is not equal to the marginal distribution of the reference process at time $T$. In this scenario, Schr\"odinger addressed the problem of identifying the Markov process with initial distribution $\pi_{0}$ and terminal distribution equal to $\pi_{T}$ which is the closest to the reference process in terms of Kullback--Leibler divergence. This special case of the so-called Schr\"odinger bridge problem can be solved using iterative proportional fitting, also known as the Sinkhorn algorithm. We leverage these ideas to develop novel Monte Carlo schemes, termed Schr\"odinger bridge samplers, to approximate a target distribution $\pi$ on $\mathbb{R}^{d}$ and to estimate its normalizing constant. This is achieved by iteratively modifying the transition kernels of the reference Markov chain to obtain a process whose marginal distribution at time $T$ becomes closer to $\pi_T = \pi$, via regression-based approximations of the corresponding iterative proportional fitting recursion. We report preliminary experiments and make connections with other problems arising in the optimal transport, optimal control and physics literatures.

Localised Generative Flows

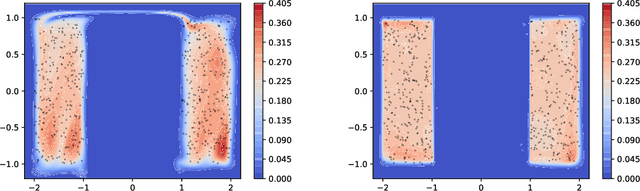
We argue that flow-based density models based on continuous bijections are limited in their ability to learn target distributions with complicated topologies, and propose Localised Generative Flows (LGFs) to address this problem. LGFs are composed of stacked continuous mixtures of bijections, which enables each bijection to learn a local region of the target rather than its entirety. Our method is a generalisation of existing flow-based methods, which can be used without modification as the basis for an LGF model. Unlike normalising flows, LGFs do not permit exact computation of log likelihoods, but we propose a simple variational scheme that performs well in practice. We show empirically that LGFs yield improved performance across a variety of density estimation tasks.

Modular Meta-Learning with Shrinkage

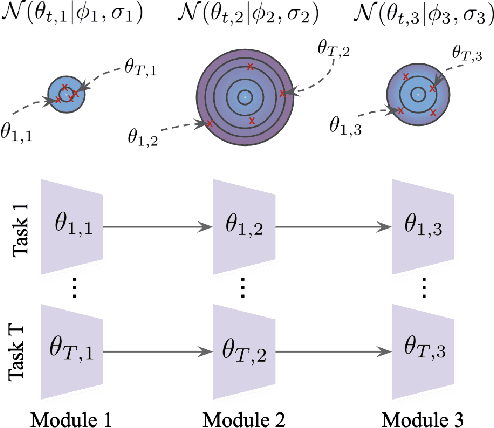
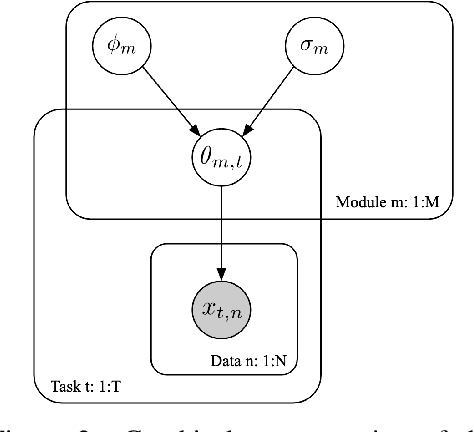
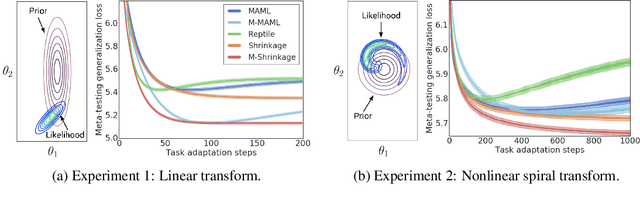
Most gradient-based approaches to meta-learning do not explicitly account for the fact that different parts of the underlying model adapt by different amounts when applied to a new task. For example, the input layers of an image classification convnet typically adapt very little, while the output layers can change significantly. This can cause parts of the model to begin to overfit while others underfit. To address this, we introduce a hierarchical Bayesian model with per-module shrinkage parameters, which we propose to learn by maximizing an approximation of the predictive likelihood using implicit differentiation. Our algorithm subsumes Reptile and outperforms variants of MAML on two synthetic few-shot meta-learning problems.

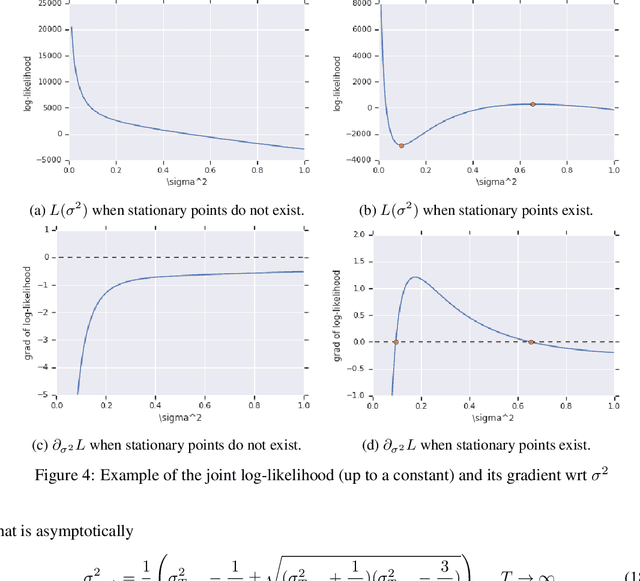
Training Dynamics of Deep Networks using Stochastic Gradient Descent via Neural Tangent Kernel

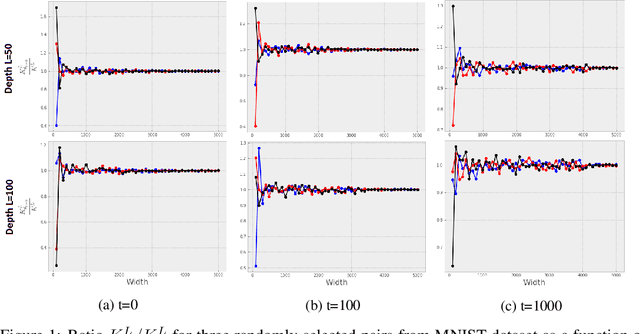
Stochastic Gradient Descent (SGD) is widely used to train deep neural networks. However, few theoretical results on the training dynamics of SGD are available. Recent work by Jacot et al. (2018) has showed that training a neural network of any kind with a full batch gradient descent in parameter space is equivalent to kernel gradient descent in function space with respect to the Neural Tangent Kernel (NTK). Lee et al. (2019) built on this result to show that the output of a neural network trained using full batch gradient descent can be approximated by a linear model for wide neural networks. We show here how these results can be extended to SGD. In this case, the resulting training dynamics is given by a stochastic differential equation dependent on the NTK which becomes a simple mean-reverting process for the squared loss. When the network depth is also large, we provide a comprehensive analysis on the impact of the initialization and the activation function on the NTK, and thus on the corresponding training dynamics under SGD. We provide experiments illustrating our theoretical results.

Efficient MCMC Sampling with Dimension-Free Convergence Rate using ADMM-type Splitting

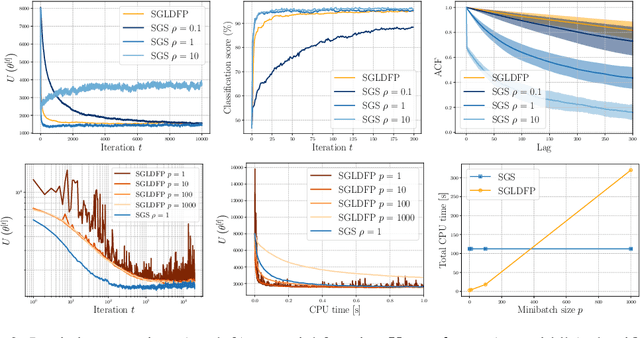
Performing exact Bayesian inference for complex models is intractable. Markov chain Monte Carlo (MCMC) algorithms can provide reliable approximations of the posterior distribution but are computationally expensive for large datasets. A standard approach to mitigate this complexity consists of using subsampling techniques or distributing the data across a cluster. However, these approaches are typically unreliable in high-dimensional scenarios. We focus here on an alternative class of MCMC schemes exploiting a splitting strategy akin to the one used by the celebrated ADMM optimization algorithm. These methods, proposed recently in [43, 51], appear to provide empirically state-of-the-art performance. We generalize here these ideas and propose a detailed theoretical study of one of these algorithms known as the Split Gibbs Sampler. Under regularity conditions, we establish explicit dimension-free convergence rates for this scheme using Ricci curvature and coupling ideas. We demonstrate experimentally the excellent performance of these MCMC schemes on various applications.

Augmented Neural ODEs

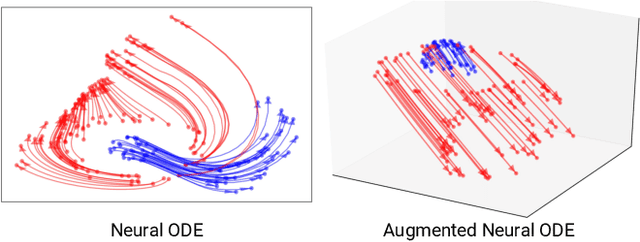
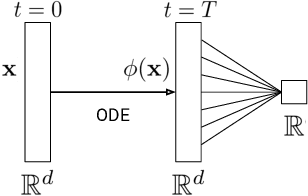
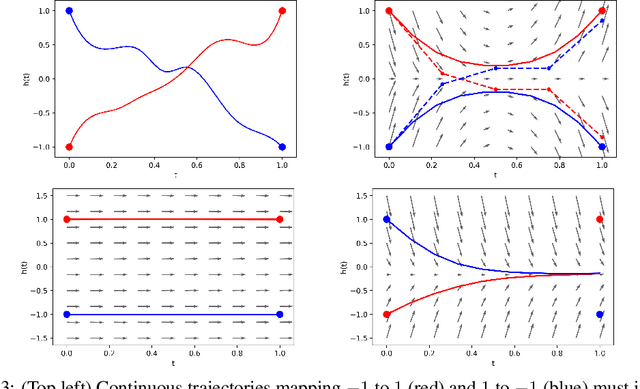
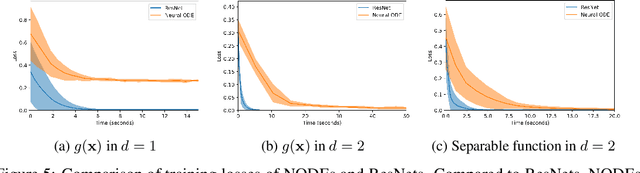
We show that Neural Ordinary Differential Equations (ODEs) learn representations that preserve the topology of the input space and prove that this implies the existence of functions Neural ODEs cannot represent. To address these limitations, we introduce Augmented Neural ODEs which, in addition to being more expressive models, are empirically more stable, generalize better and have a lower computational cost than Neural ODEs.

Bernoulli Race Particle Filters

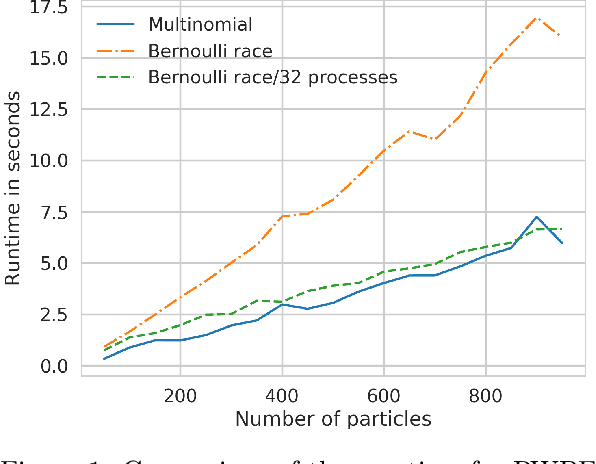
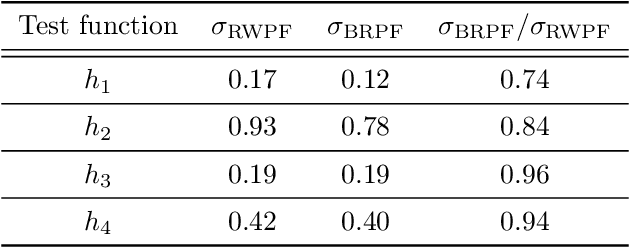
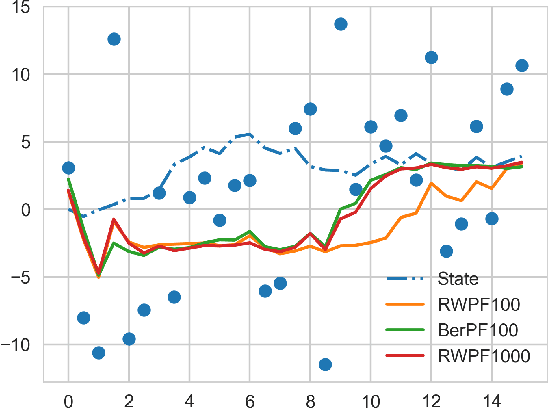
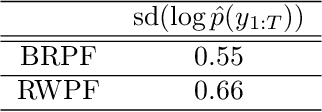
When the weights in a particle filter are not available analytically, standard resampling methods cannot be employed. To circumvent this problem state-of-the-art algorithms replace the true weights with non-negative unbiased estimates. This algorithm is still valid but at the cost of higher variance of the resulting filtering estimates in comparison to a particle filter using the true weights. We propose here a novel algorithm that allows for resampling according to the true intractable weights when only an unbiased estimator of the weights is available. We demonstrate our algorithm on several examples.

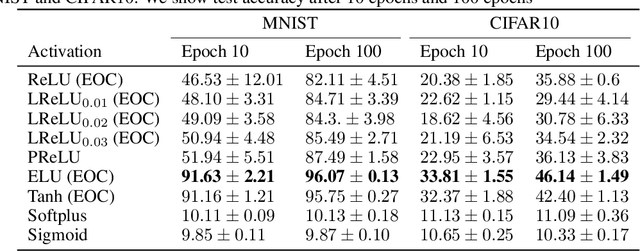
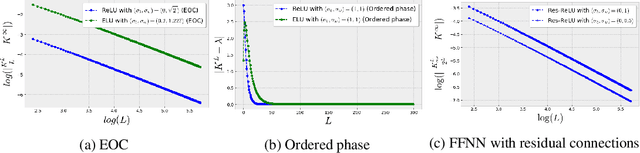
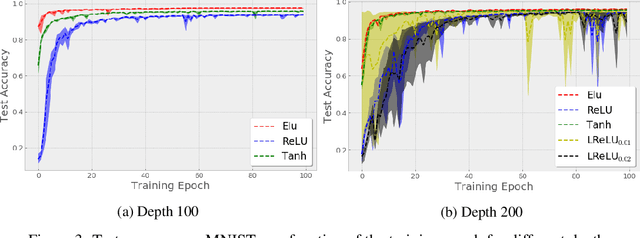
On the Impact of the Activation Function on Deep Neural Networks Training

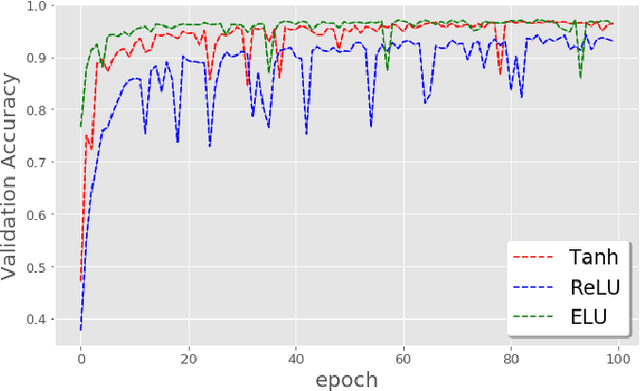
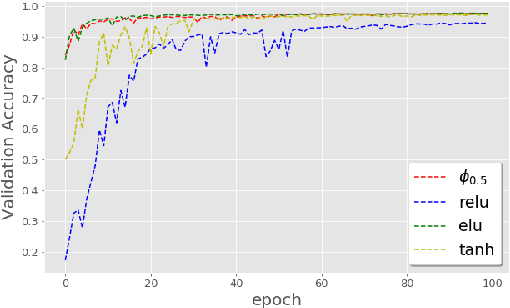
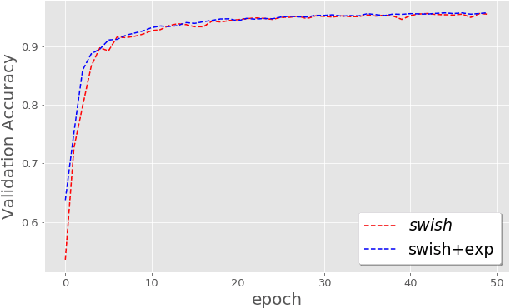
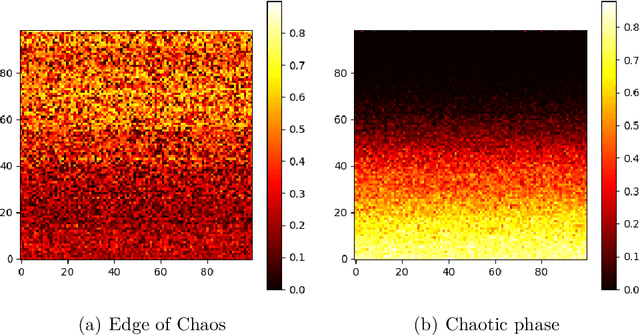
The weight initialization and the activation function of deep neural networks have a crucial impact on the performance of the training procedure. An inappropriate selection can lead to the loss of information of the input during forward propagation and the exponential vanishing/exploding of gradients during back-propagation. Understanding the theoretical properties of untrained random networks is key to identifying which deep networks may be trained successfully as recently demonstrated by Samuel et al (2017) who showed that for deep feedforward neural networks only a specific choice of hyperparameters known as the `Edge of Chaos' can lead to good performance. While the work by Samuel et al (2017) discuss trainability issues, we focus here on training acceleration and overall performance. We give a comprehensive theoretical analysis of the Edge of Chaos and show that we can indeed tune the initialization parameters and the activation function in order to accelerate the training and improve the performance.