Importance Weighting Approach in Kernel Bayes' Rule

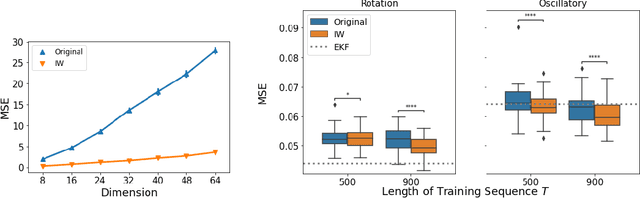
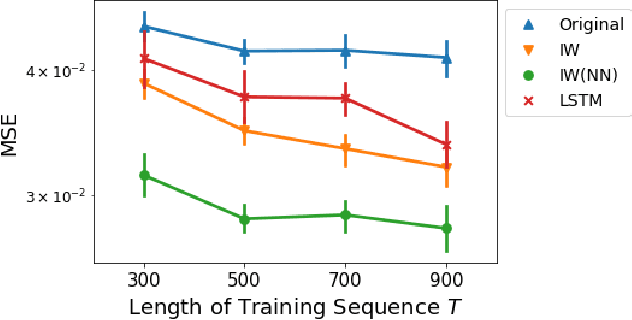
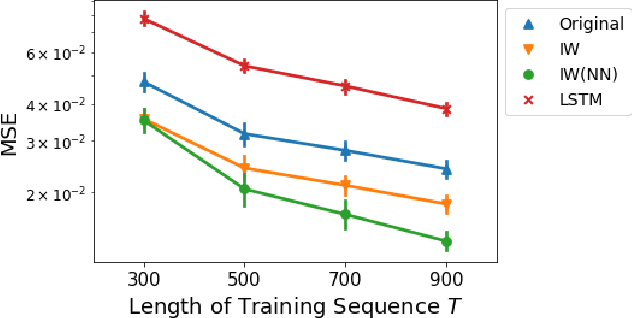
We study a nonparametric approach to Bayesian computation via feature means, where the expectation of prior features is updated to yield expected posterior features, based on regression from kernel or neural net features of the observations. All quantities involved in the Bayesian update are learned from observed data, making the method entirely model-free. The resulting algorithm is a novel instance of a kernel Bayes' rule (KBR). Our approach is based on importance weighting, which results in superior numerical stability to the existing approach to KBR, which requires operator inversion. We show the convergence of the estimator using a novel consistency analysis on the importance weighting estimator in the infinity norm. We evaluate our KBR on challenging synthetic benchmarks, including a filtering problem with a state-space model involving high dimensional image observations. The proposed method yields uniformly better empirical performance than the existing KBR, and competitive performance with other competing methods.

Continual Repeated Annealed Flow Transport Monte Carlo

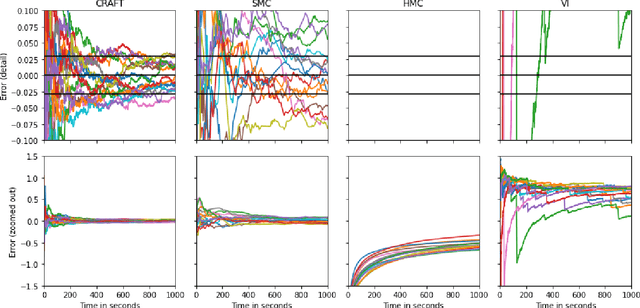
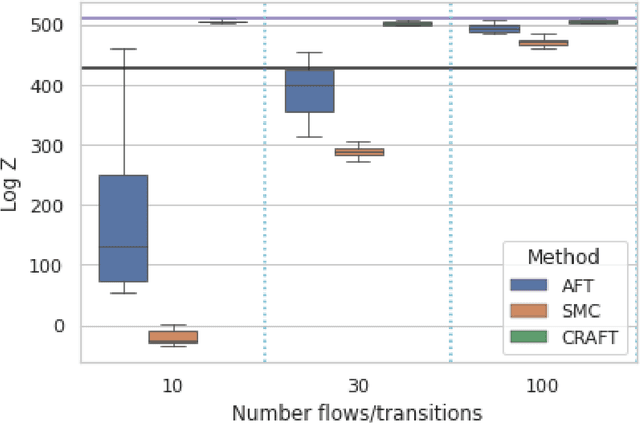
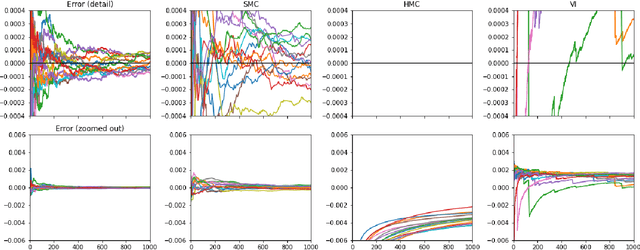
We propose Continual Repeated Annealed Flow Transport Monte Carlo (CRAFT), a method that combines a sequential Monte Carlo (SMC) sampler (itself a generalization of Annealed Importance Sampling) with variational inference using normalizing flows. The normalizing flows are directly trained to transport between annealing temperatures using a KL divergence for each transition. This optimization objective is itself estimated using the normalizing flow/SMC approximation. We show conceptually and using multiple empirical examples that CRAFT improves on Annealed Flow Transport Monte Carlo (Arbel et al., 2021), on which it builds and also on Markov chain Monte Carlo (MCMC) based Stochastic Normalizing Flows (Wu et al., 2020). By incorporating CRAFT within particle MCMC, we show that such learnt samplers can achieve impressively accurate results on a challenging lattice field theory example.

COIN++: Data Agnostic Neural Compression

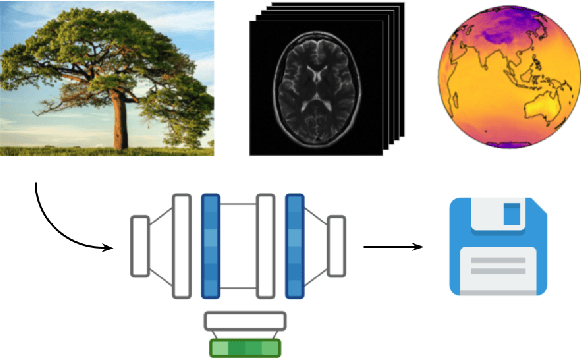
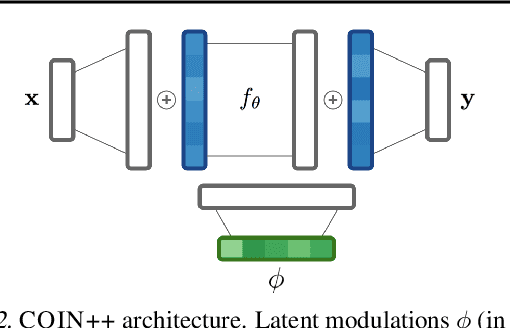
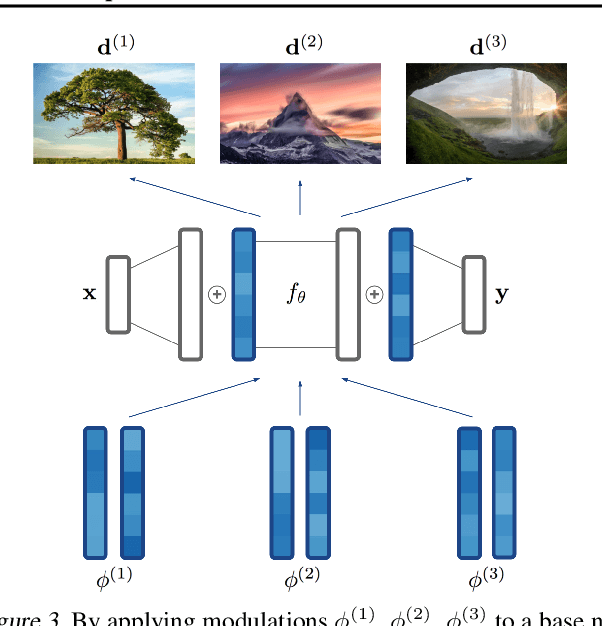
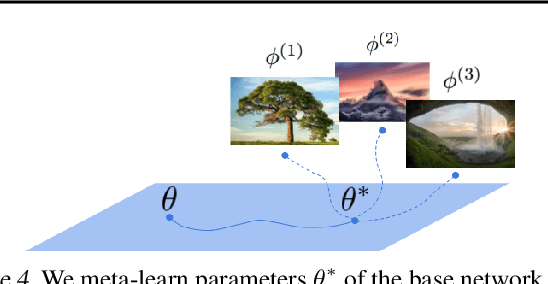
Neural compression algorithms are typically based on autoencoders that require specialized encoder and decoder architectures for different data modalities. In this paper, we propose COIN++, a neural compression framework that seamlessly handles a wide range of data modalities. Our approach is based on converting data to implicit neural representations, i.e. neural functions that map coordinates (such as pixel locations) to features (such as RGB values). Then, instead of storing the weights of the implicit neural representation directly, we store modulations applied to a meta-learned base network as a compressed code for the data. We further quantize and entropy code these modulations, leading to large compression gains while reducing encoding time by two orders of magnitude compared to baselines. We empirically demonstrate the effectiveness of our method by compressing various data modalities, from images to medical and climate data.

Simulating Diffusion Bridges with Score Matching

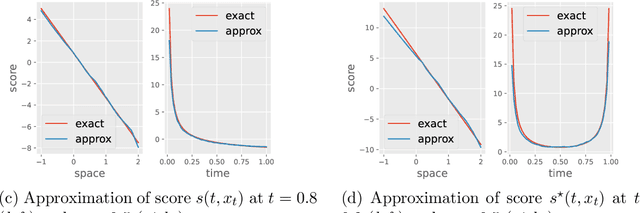
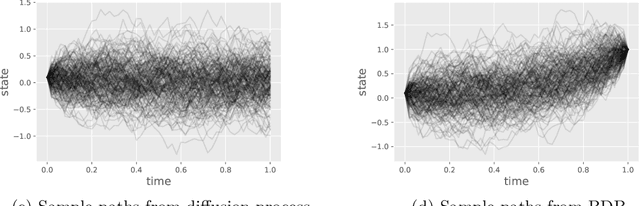
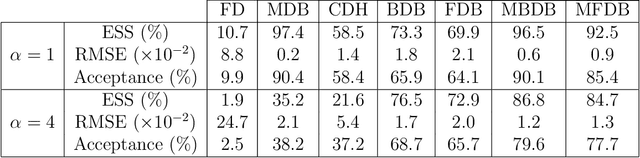
We consider the problem of simulating diffusion bridges, i.e. diffusion processes that are conditioned to initialize and terminate at two given states. Diffusion bridge simulation has applications in diverse scientific fields and plays a crucial role for statistical inference of discretely-observed diffusions. This is known to be a challenging problem that has received much attention in the last two decades. In this work, we first show that the time-reversed diffusion bridge process can be simulated if one can time-reverse the unconditioned diffusion process. We introduce a variational formulation to learn this time-reversal that relies on a score matching method to circumvent intractability. We then consider another iteration of our proposed methodology to approximate the Doob's $h$-transform defining the diffusion bridge process. As our approach is generally applicable under mild assumptions on the underlying diffusion process, it can easily be used to improve the proposal bridge process within existing methods and frameworks. We discuss algorithmic considerations and extensions, and present some numerical results.

Online Variational Filtering and Parameter Learning

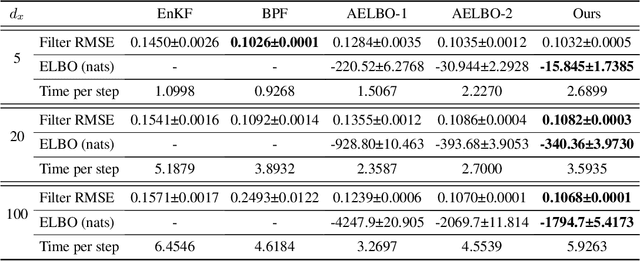
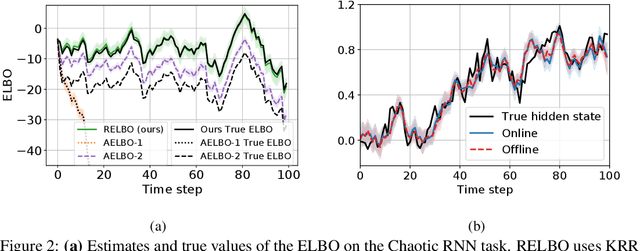
We present a variational method for online state estimation and parameter learning in state-space models (SSMs), a ubiquitous class of latent variable models for sequential data. As per standard batch variational techniques, we use stochastic gradients to simultaneously optimize a lower bound on the log evidence with respect to both model parameters and a variational approximation of the states' posterior distribution. However, unlike existing approaches, our method is able to operate in an entirely online manner, such that historic observations do not require revisitation after being incorporated and the cost of updates at each time step remains constant, despite the growing dimensionality of the joint posterior distribution of the states. This is achieved by utilizing backward decompositions of this joint posterior distribution and of its variational approximation, combined with Bellman-type recursions for the evidence lower bound and its gradients. We demonstrate the performance of this methodology across several examples, including high-dimensional SSMs and sequential Variational Auto-Encoders.

Conditional Gaussian PAC-Bayes

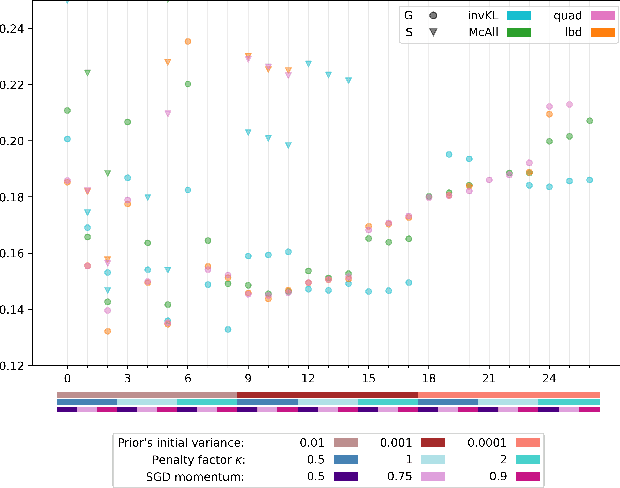
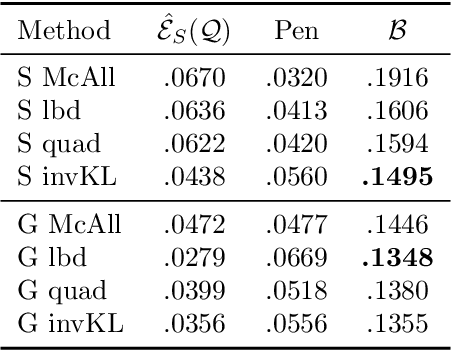
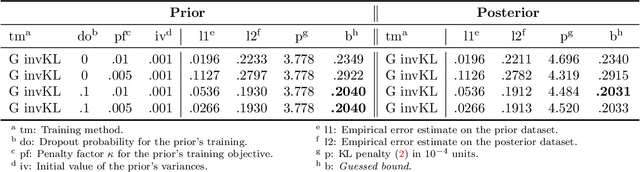
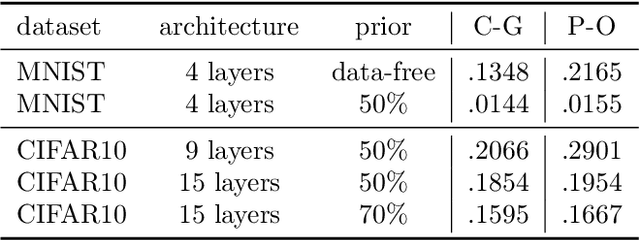
Recent studies have empirically investigated different methods to train a stochastic classifier by optimising a PAC-Bayesian bound via stochastic gradient descent. Most of these procedures need to replace the misclassification error with a surrogate loss, leading to a mismatch between the optimisation objective and the actual generalisation bound. The present paper proposes a novel training algorithm that optimises the PAC-Bayesian bound, without relying on any surrogate loss. Empirical results show that the bounds obtained with this approach are tighter than those found in the literature.

Learning Optimal Conformal Classifiers

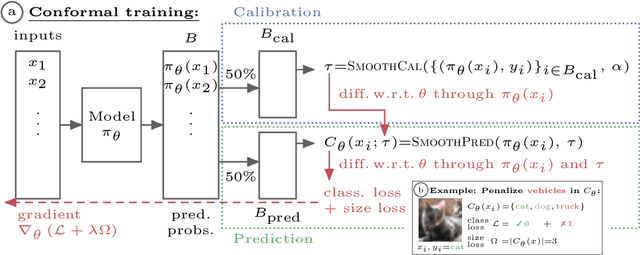
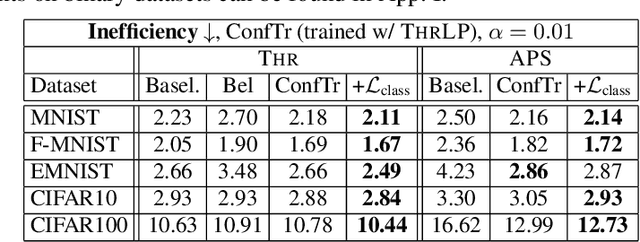
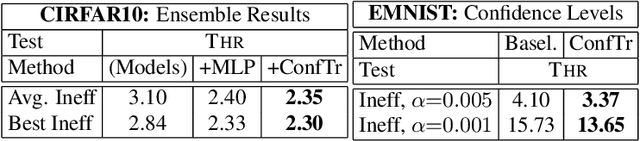
Modern deep learning based classifiers show very high accuracy on test data but this does not provide sufficient guarantees for safe deployment, especially in high-stake AI applications such as medical diagnosis. Usually, predictions are obtained without a reliable uncertainty estimate or a formal guarantee. Conformal prediction (CP) addresses these issues by using the classifier's probability estimates to predict confidence sets containing the true class with a user-specified probability. However, using CP as a separate processing step after training prevents the underlying model from adapting to the prediction of confidence sets. Thus, this paper explores strategies to differentiate through CP during training with the goal of training model with the conformal wrapper end-to-end. In our approach, conformal training (ConfTr), we specifically "simulate" conformalization on mini-batches during training. We show that CT outperforms state-of-the-art CP methods for classification by reducing the average confidence set size (inefficiency). Moreover, it allows to "shape" the confidence sets predicted at test time, which is difficult for standard CP. On experiments with several datasets, we show ConfTr can influence how inefficiency is distributed across classes, or guide the composition of confidence sets in terms of the included classes, while retaining the guarantees offered by CP.

Bias Mitigated Learning from Differentially Private Synthetic Data: A Cautionary Tale

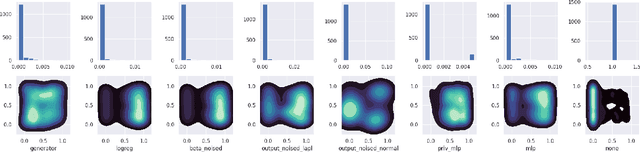
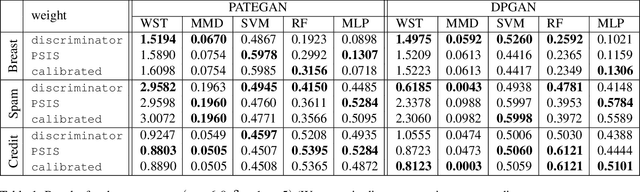
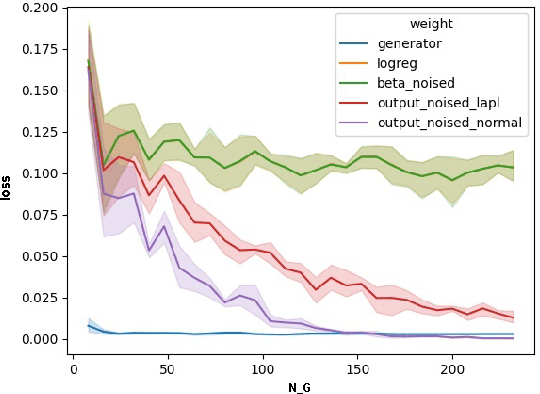
Increasing interest in privacy-preserving machine learning has led to new models for synthetic private data generation from undisclosed real data. However, mechanisms of privacy preservation introduce artifacts in the resulting synthetic data that have a significant impact on downstream tasks such as learning predictive models or inference. In particular, bias can affect all analyses as the synthetic data distribution is an inconsistent estimate of the real-data distribution. We propose several bias mitigation strategies using privatized likelihood ratios that have general applicability to differentially private synthetic data generative models. Through large-scale empirical evaluation, we show that bias mitigation provides simple and effective privacy-compliant augmentation for general applications of synthetic data. However, the work highlights that even after bias correction significant challenges remain on the usefulness of synthetic private data generators for tasks such as prediction and inference.

Quantitative Uniform Stability of the Iterative Proportional Fitting Procedure

We establish the uniform in time stability, w.r.t. the marginals, of the Iterative Proportional Fitting Procedure, also known as Sinkhorn algorithm, used to solve entropy-regularised Optimal Transport problems. Our result is quantitative and stated in terms of the 1-Wasserstein metric. As a corollary we establish a quantitative stability result for Schr\"odinger bridges.

Monte Carlo Variational Auto-Encoders

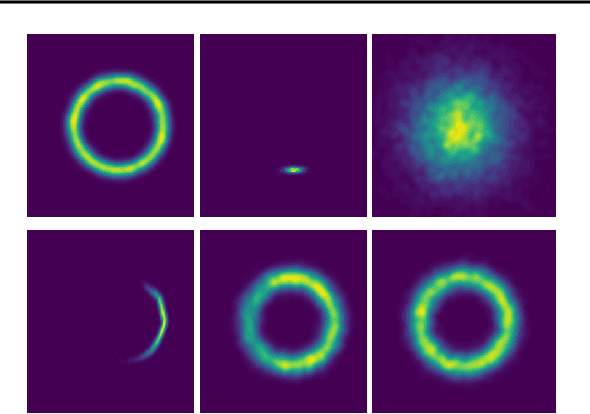
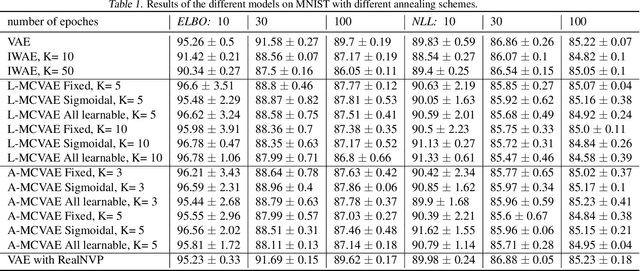
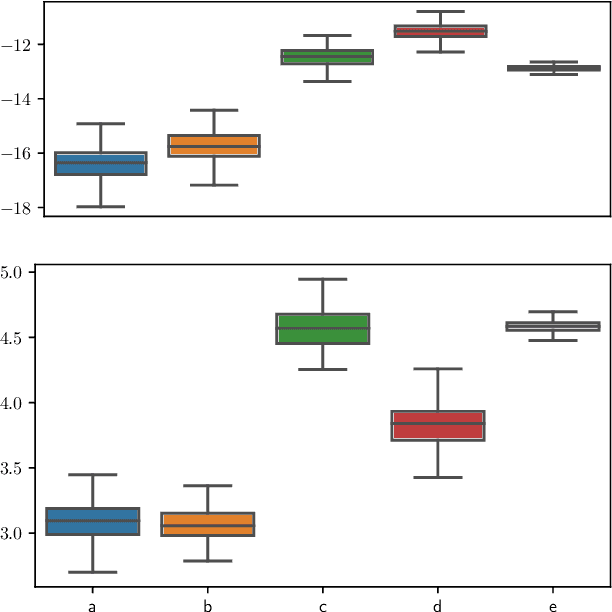
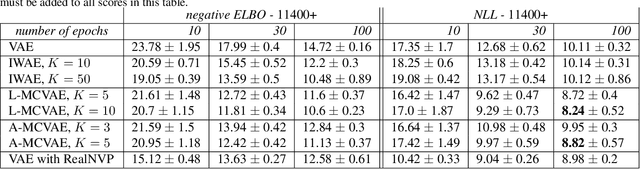
Variational auto-encoders (VAE) are popular deep latent variable models which are trained by maximizing an Evidence Lower Bound (ELBO). To obtain tighter ELBO and hence better variational approximations, it has been proposed to use importance sampling to get a lower variance estimate of the evidence. However, importance sampling is known to perform poorly in high dimensions. While it has been suggested many times in the literature to use more sophisticated algorithms such as Annealed Importance Sampling (AIS) and its Sequential Importance Sampling (SIS) extensions, the potential benefits brought by these advanced techniques have never been realized for VAE: the AIS estimate cannot be easily differentiated, while SIS requires the specification of carefully chosen backward Markov kernels. In this paper, we address both issues and demonstrate the performance of the resulting Monte Carlo VAEs on a variety of applications.