Provable Partially Observable Reinforcement Learning with Privileged Information

Partial observability of the underlying states generally presents significant challenges for reinforcement learning (RL). In practice, certain \emph{privileged information}, e.g., the access to states from simulators, has been exploited in training and has achieved prominent empirical successes. To better understand the benefits of privileged information, we revisit and examine several simple and practically used paradigms in this setting. Specifically, we first formalize the empirical paradigm of \emph{expert distillation} (also known as \emph{teacher-student} learning), demonstrating its pitfall in finding near-optimal policies. We then identify a condition of the partially observable environment, the \emph{deterministic filter condition}, under which expert distillation achieves sample and computational complexities that are \emph{both} polynomial. Furthermore, we investigate another useful empirical paradigm of \emph{asymmetric actor-critic}, and focus on the more challenging setting of observable partially observable Markov decision processes. We develop a belief-weighted asymmetric actor-critic algorithm with polynomial sample and quasi-polynomial computational complexities, in which one key component is a new provable oracle for learning belief states that preserve \emph{filter stability} under a misspecified model, which may be of independent interest. Finally, we also investigate the provable efficiency of partially observable multi-agent RL (MARL) with privileged information. We develop algorithms featuring \emph{centralized-training-with-decentralized-execution}, a popular framework in empirical MARL, with polynomial sample and (quasi-)polynomial computational complexities in both paradigms above. Compared with a few recent related theoretical studies, our focus is on understanding practically inspired algorithmic paradigms, without computationally intractable oracles.

COMAL: A Convergent Meta-Algorithm for Aligning LLMs with General Preferences

Many alignment methods, including reinforcement learning from human feedback (RLHF), rely on the Bradley-Terry reward assumption, which is insufficient to capture the full range of general human preferences. To achieve robust alignment with general preferences, we model the alignment problem as a two-player zero-sum game, where the Nash equilibrium policy guarantees a 50% win rate against any competing policy. However, previous algorithms for finding the Nash policy either diverge or converge to a Nash policy in a modified game, even in a simple synthetic setting, thereby failing to maintain the 50% win rate guarantee against all other policies. We propose a meta-algorithm, Convergent Meta Alignment Algorithm (COMAL), for language model alignment with general preferences, inspired by convergent algorithms in game theory. Theoretically, we prove that our meta-algorithm converges to an exact Nash policy in the last iterate. Additionally, our meta-algorithm is simple and can be integrated with many existing methods designed for RLHF and preference optimization with minimal changes. Experimental results demonstrate the effectiveness of the proposed framework when combined with existing preference policy optimization methods.

Injecting Undetectable Backdoors in Deep Learning and Language Models

As ML models become increasingly complex and integral to high-stakes domains such as finance and healthcare, they also become more susceptible to sophisticated adversarial attacks. We investigate the threat posed by undetectable backdoors in models developed by insidious external expert firms. When such backdoors exist, they allow the designer of the model to sell information to the users on how to carefully perturb the least significant bits of their input to change the classification outcome to a favorable one. We develop a general strategy to plant a backdoor to neural networks while ensuring that even if the model's weights and architecture are accessible, the existence of the backdoor is still undetectable. To achieve this, we utilize techniques from cryptography such as cryptographic signatures and indistinguishability obfuscation. We further introduce the notion of undetectable backdoors to language models and extend our neural network backdoor attacks to such models based on the existence of steganographic functions.

Curvature-Independent Last-Iterate Convergence for Games on Riemannian Manifolds

Numerous applications in machine learning and data analytics can be formulated as equilibrium computation over Riemannian manifolds. Despite the extensive investigation of their Euclidean counterparts, the performance of Riemannian gradient-based algorithms remain opaque and poorly understood. We revisit the original scheme of Riemannian gradient descent (RGD) and analyze it under a geodesic monotonicity assumption, which includes the well-studied geodesically convex-concave min-max optimization problem as a special case. Our main contribution is to show that, despite the phenomenon of distance distortion, the RGD scheme, with a step size that is agnostic to the manifold's curvature, achieves a curvature-independent and linear last-iterate convergence rate in the geodesically strongly monotone setting. To the best of our knowledge, the possibility of curvature-independent rates and/or last-iterate convergence in the Riemannian setting has not been considered before.

Accelerated Algorithms for Monotone Inclusions and Constrained Nonconvex-Nonconcave Min-Max Optimization

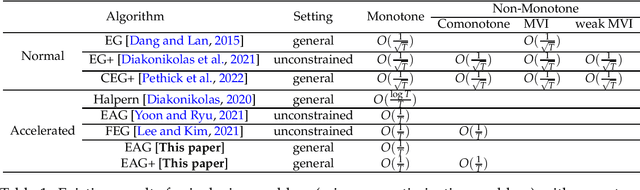
We study monotone inclusions and monotone variational inequalities, as well as their generalizations to non-monotone settings. We first show that the Extra Anchored Gradient (EAG) algorithm, originally proposed by Yoon and Ryu [2021] for unconstrained convex-concave min-max optimization, can be applied to solve the more general problem of Lipschitz monotone inclusion. More specifically, we prove that the EAG solves Lipschitz monotone inclusion problems with an \emph{accelerated convergence rate} of $O(\frac{1}{T})$, which is \emph{optimal among all first-order methods} [Diakonikolas, 2020, Yoon and Ryu, 2021]. Our second result is a new algorithm, called Extra Anchored Gradient Plus (EAG+), which not only achieves the accelerated $O(\frac{1}{T})$ convergence rate for all monotone inclusion problems, but also exhibits the same accelerated rate for a family of general (non-monotone) inclusion problems that concern negative comonotone operators. As a special case of our second result, EAG+ enjoys the $O(\frac{1}{T})$ convergence rate for solving a non-trivial class of nonconvex-nonconcave min-max optimization problems. Our analyses are based on simple potential function arguments, which might be useful for analysing other accelerated algorithms.

Tight Last-Iterate Convergence of the Extragradient Method for Constrained Monotone Variational Inequalities

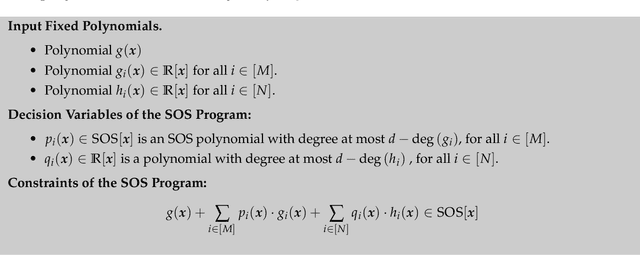
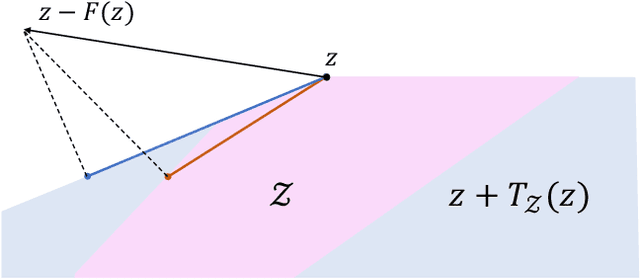
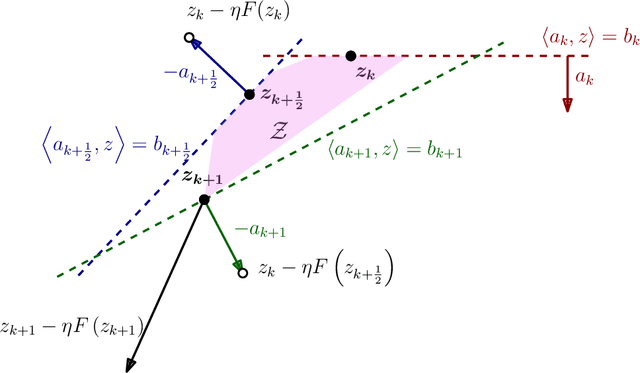
The monotone variational inequality is a central problem in mathematical programming that unifies and generalizes many important settings such as smooth convex optimization, two-player zero-sum games, convex-concave saddle point problems, etc. The extragradient method by Korpelevich [1976] is one of the most popular methods for solving monotone variational inequalities. Despite its long history and intensive attention from the optimization and machine learning community, the following major problem remains open. What is the last-iterate convergence rate of the extragradient method for monotone and Lipschitz variational inequalities with constraints? We resolve this open problem by showing a tight $O\left(\frac{1}{\sqrt{T}}\right)$ last-iterate convergence rate for arbitrary convex feasible sets, which matches the lower bound by Golowich et al. [2020]. Our rate is measured in terms of the standard gap function. The technical core of our result is the monotonicity of a new performance measure -- the tangent residual, which can be viewed as an adaptation of the norm of the operator that takes the local constraints into account. To establish the monotonicity, we develop a new approach that combines the power of the sum-of-squares programming with the low dimensionality of the update rule of the extragradient method. We believe our approach has many additional applications in the analysis of iterative methods.