Generative flow-based warm start of the variational quantum eigensolver

Hybrid quantum-classical algorithms like the variational quantum eigensolver (VQE) show promise for quantum simulations on near-term quantum devices, but are often limited by complex objective functions and expensive optimization procedures. Here, we propose Flow-VQE, a generative framework leveraging conditional normalizing flows with parameterized quantum circuits to efficiently generate high-quality variational parameters. By embedding a generative model into the VQE optimization loop through preference-based training, Flow-VQE enables quantum gradient-free optimization and offers a systematic approach for parameter transfer, accelerating convergence across related problems through warm-started optimization. We compare Flow-VQE to a number of standard benchmarks through numerical simulations on molecular systems, including hydrogen chains, water, ammonia, and benzene. We find that Flow-VQE outperforms baseline optimization algorithms, achieving computational accuracy with fewer circuit evaluations (improvements range from modest to more than two orders of magnitude) and, when used to warm-start the optimization of new systems, accelerates subsequent fine-tuning by up to 50-fold compared with Hartree--Fock initialization. Therefore, we believe Flow-VQE can become a pragmatic and versatile paradigm for leveraging generative modeling to reduce the costs of variational quantum algorithms.

Quantum computing and artificial intelligence: status and perspectives

This white paper discusses and explores the various points of intersection between quantum computing and artificial intelligence (AI). It describes how quantum computing could support the development of innovative AI solutions. It also examines use cases of classical AI that can empower research and development in quantum technologies, with a focus on quantum computing and quantum sensing. The purpose of this white paper is to provide a long-term research agenda aimed at addressing foundational questions about how AI and quantum computing interact and benefit one another. It concludes with a set of recommendations and challenges, including how to orchestrate the proposed theoretical work, align quantum AI developments with quantum hardware roadmaps, estimate both classical and quantum resources - especially with the goal of mitigating and optimizing energy consumption - advance this emerging hybrid software engineering discipline, and enhance European industrial competitiveness while considering societal implications.

Gradient-descent quantum process tomography by learning Kraus operators

We perform quantum process tomography (QPT) for both discrete- and continuous-variable quantum systems by learning a process representation using Kraus operators. The Kraus form ensures that the reconstructed process is completely positive. To make the process trace-preserving, we use a constrained gradient-descent (GD) approach on the so-called Stiefel manifold during optimization to obtain the Kraus operators. Our ansatz uses a few Kraus operators to avoid direct estimation of large process matrices, e.g., the Choi matrix, for low-rank quantum processes. The GD-QPT matches the performance of both compressed-sensing (CS) and projected least-squares (PLS) QPT in benchmarks with two-qubit random processes, but shines by combining the best features of these two methods. Similar to CS (but unlike PLS), GD-QPT can reconstruct a process from just a small number of random measurements, and similar to PLS (but unlike CS) it also works for larger system sizes, up to at least five qubits. We envisage that the data-driven approach of GD-QPT can become a practical tool that greatly reduces the cost and computational effort for QPT in intermediate-scale quantum systems.

Classification and reconstruction of optical quantum states with deep neural networks

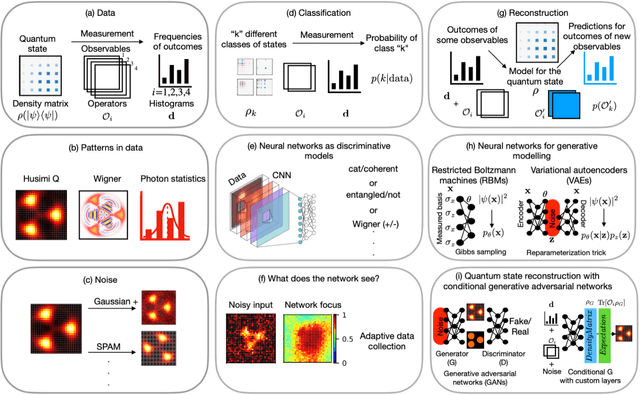
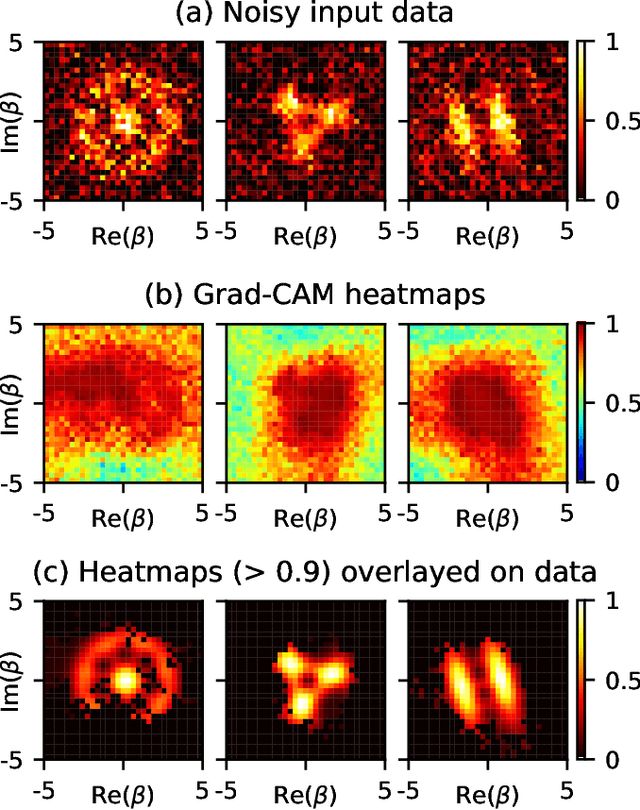
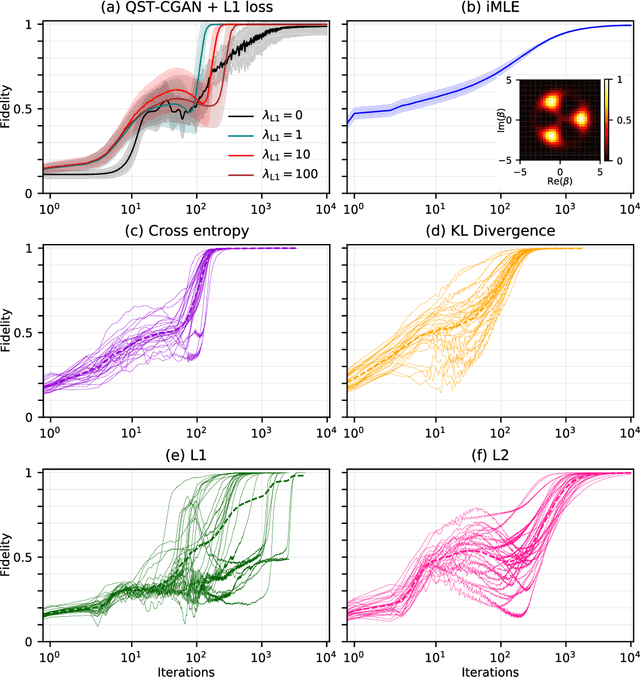
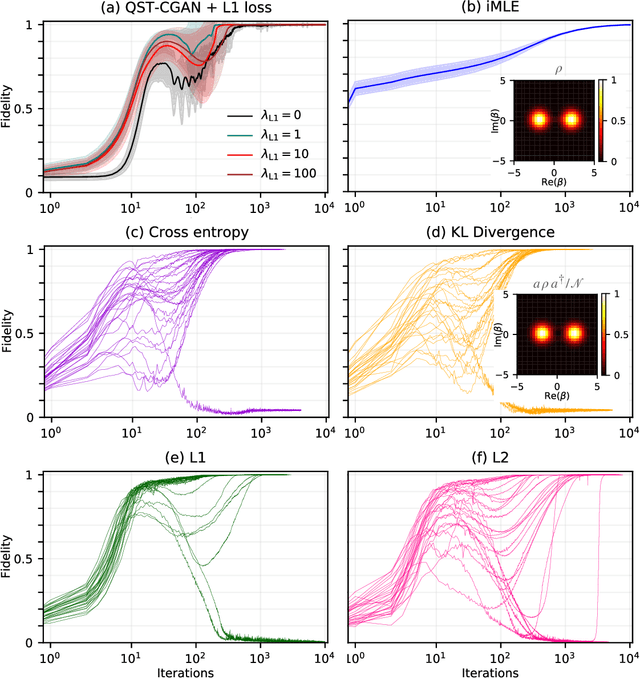
We apply deep-neural-network-based techniques to quantum state classification and reconstruction. We demonstrate high classification accuracies and reconstruction fidelities, even in the presence of noise and with little data. Using optical quantum states as examples, we first demonstrate how convolutional neural networks (CNNs) can successfully classify several types of states distorted by, e.g., additive Gaussian noise or photon loss. We further show that a CNN trained on noisy inputs can learn to identify the most important regions in the data, which potentially can reduce the cost of tomography by guiding adaptive data collection. Secondly, we demonstrate reconstruction of quantum-state density matrices using neural networks that incorporate quantum-physics knowledge. The knowledge is implemented as custom neural-network layers that convert outputs from standard feedforward neural networks to valid descriptions of quantum states. Any standard feed-forward neural-network architecture can be adapted for quantum state tomography (QST) with our method. We present further demonstrations of our proposed [arXiv:2008.03240] QST technique with conditional generative adversarial networks (QST-CGAN). We motivate our choice of a learnable loss function within an adversarial framework by demonstrating that the QST-CGAN outperforms, across a range of scenarios, generative networks trained with standard loss functions. For pure states with additive or convolutional Gaussian noise, the QST-CGAN is able to adapt to the noise and reconstruct the underlying state. The QST-CGAN reconstructs states using up to two orders of magnitude fewer iterative steps than a standard iterative maximum likelihood (iMLE) method. Further, the QST-CGAN can reconstruct both pure and mixed states from two orders of magnitude fewer randomly chosen data points than iMLE.

Quantum State Tomography with Conditional Generative Adversarial Networks

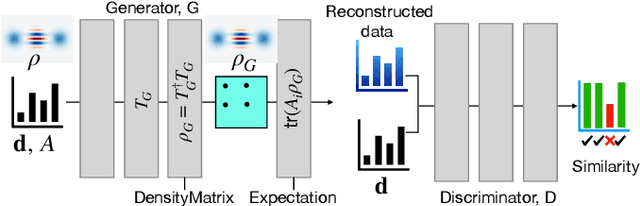
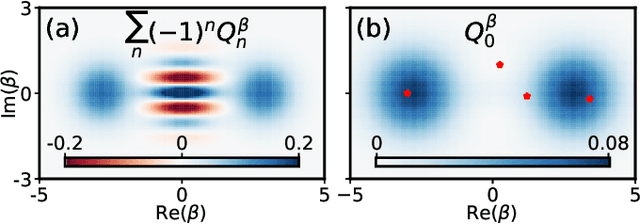
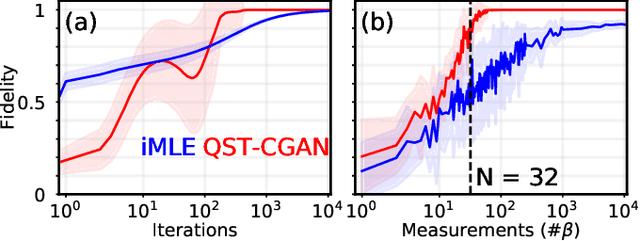
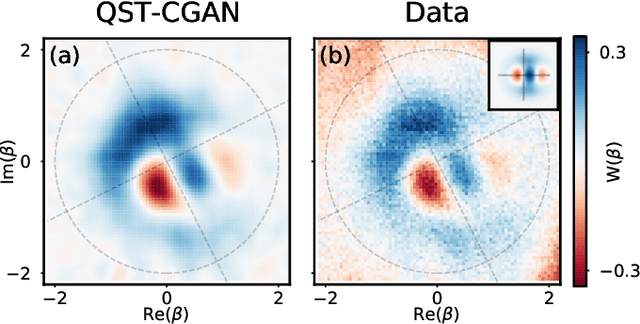
Quantum state tomography (QST) is a challenging task in intermediate-scale quantum devices. Here, we apply conditional generative adversarial networks (CGANs) to QST. In the CGAN framework, two duelling neural networks, a generator and a discriminator, learn multi-modal models from data. We augment a CGAN with custom neural-network layers that enable conversion of output from any standard neural network into a physical density matrix. To reconstruct the density matrix, the generator and discriminator networks train each other on data using standard gradient-based methods. We demonstrate that our QST-CGAN reconstructs optical quantum states with high fidelity orders of magnitude faster, and from less data, than a standard maximum-likelihood method. We also show that the QST-CGAN can reconstruct a quantum state in a single evaluation of the generator network if it has been pre-trained on similar quantum states.