Diffusion Model Predictive Control

We propose Diffusion Model Predictive Control (D-MPC), a novel MPC approach that learns a multi-step action proposal and a multi-step dynamics model, both using diffusion models, and combines them for use in online MPC. On the popular D4RL benchmark, we show performance that is significantly better than existing model-based offline planning methods using MPC and competitive with state-of-the-art (SOTA) model-based and model-free reinforcement learning methods. We additionally illustrate D-MPC's ability to optimize novel reward functions at run time and adapt to novel dynamics, and highlight its advantages compared to existing diffusion-based planning baselines.

DMC-VB: A Benchmark for Representation Learning for Control with Visual Distractors

Learning from previously collected data via behavioral cloning or offline reinforcement learning (RL) is a powerful recipe for scaling generalist agents by avoiding the need for expensive online learning. Despite strong generalization in some respects, agents are often remarkably brittle to minor visual variations in control-irrelevant factors such as the background or camera viewpoint. In this paper, we present theDeepMind Control Visual Benchmark (DMC-VB), a dataset collected in the DeepMind Control Suite to evaluate the robustness of offline RL agents for solving continuous control tasks from visual input in the presence of visual distractors. In contrast to prior works, our dataset (a) combines locomotion and navigation tasks of varying difficulties, (b) includes static and dynamic visual variations, (c) considers data generated by policies with different skill levels, (d) systematically returns pairs of state and pixel observation, (e) is an order of magnitude larger, and (f) includes tasks with hidden goals. Accompanying our dataset, we propose three benchmarks to evaluate representation learning methods for pretraining, and carry out experiments on several recently proposed methods. First, we find that pretrained representations do not help policy learning on DMC-VB, and we highlight a large representation gap between policies learned on pixel observations and on states. Second, we demonstrate when expert data is limited, policy learning can benefit from representations pretrained on (a) suboptimal data, and (b) tasks with stochastic hidden goals. Our dataset and benchmark code to train and evaluate agents are available at: https://github.com/google-deepmind/dmc_vision_benchmark.

Learning Cognitive Maps from Transformer Representations for Efficient Planning in Partially Observed Environments

Despite their stellar performance on a wide range of tasks, including in-context tasks only revealed during inference, vanilla transformers and variants trained for next-token predictions (a) do not learn an explicit world model of their environment which can be flexibly queried and (b) cannot be used for planning or navigation. In this paper, we consider partially observed environments (POEs), where an agent receives perceptually aliased observations as it navigates, which makes path planning hard. We introduce a transformer with (multiple) discrete bottleneck(s), TDB, whose latent codes learn a compressed representation of the history of observations and actions. After training a TDB to predict the future observation(s) given the history, we extract interpretable cognitive maps of the environment from its active bottleneck(s) indices. These maps are then paired with an external solver to solve (constrained) path planning problems. First, we show that a TDB trained on POEs (a) retains the near perfect predictive performance of a vanilla transformer or an LSTM while (b) solving shortest path problems exponentially faster. Second, a TDB extracts interpretable representations from text datasets, while reaching higher in-context accuracy than vanilla sequence models. Finally, in new POEs, a TDB (a) reaches near-perfect in-context accuracy, (b) learns accurate in-context cognitive maps (c) solves in-context path planning problems.

Schema-learning and rebinding as mechanisms of in-context learning and emergence

In-context learning (ICL) is one of the most powerful and most unexpected capabilities to emerge in recent transformer-based large language models (LLMs). Yet the mechanisms that underlie it are poorly understood. In this paper, we demonstrate that comparable ICL capabilities can be acquired by an alternative sequence prediction learning method using clone-structured causal graphs (CSCGs). Moreover, a key property of CSCGs is that, unlike transformer-based LLMs, they are {\em interpretable}, which considerably simplifies the task of explaining how ICL works. Specifically, we show that it uses a combination of (a) learning template (schema) circuits for pattern completion, (b) retrieving relevant templates in a context-sensitive manner, and (c) rebinding of novel tokens to appropriate slots in the templates. We go on to marshall evidence for the hypothesis that similar mechanisms underlie ICL in LLMs. For example, we find that, with CSCGs as with LLMs, different capabilities emerge at different levels of overparameterization, suggesting that overparameterization helps in learning more complex template (schema) circuits. By showing how ICL can be achieved with small models and datasets, we open up a path to novel architectures, and take a vital step towards a more general understanding of the mechanics behind this important capability.

Learning noisy-OR Bayesian Networks with Max-Product Belief Propagation

Noisy-OR Bayesian Networks (BNs) are a family of probabilistic graphical models which express rich statistical dependencies in binary data. Variational inference (VI) has been the main method proposed to learn noisy-OR BNs with complex latent structures (Jaakkola & Jordan, 1999; Ji et al., 2020; Buhai et al., 2020). However, the proposed VI approaches either (a) use a recognition network with standard amortized inference that cannot induce ``explaining-away''; or (b) assume a simple mean-field (MF) posterior which is vulnerable to bad local optima. Existing MF VI methods also update the MF parameters sequentially which makes them inherently slow. In this paper, we propose parallel max-product as an alternative algorithm for learning noisy-OR BNs with complex latent structures and we derive a fast stochastic training scheme that scales to large datasets. We evaluate both approaches on several benchmarks where VI is the state-of-the-art and show that our method (a) achieves better test performance than Ji et al. (2020) for learning noisy-OR BNs with hierarchical latent structures on large sparse real datasets; (b) recovers a higher number of ground truth parameters than Buhai et al. (2020) from cluttered synthetic scenes; and (c) solves the 2D blind deconvolution problem from Lazaro-Gredilla et al. (2021) and variant - including binary matrix factorization - while VI catastrophically fails and is up to two orders of magnitude slower.

Graphical Models with Attention for Context-Specific Independence and an Application to Perceptual Grouping

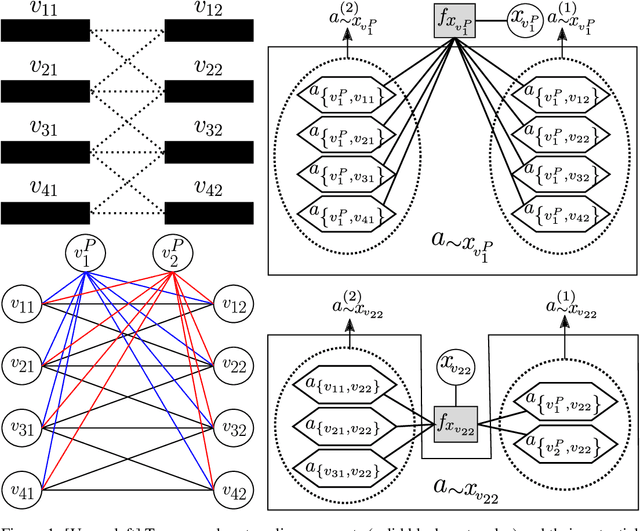
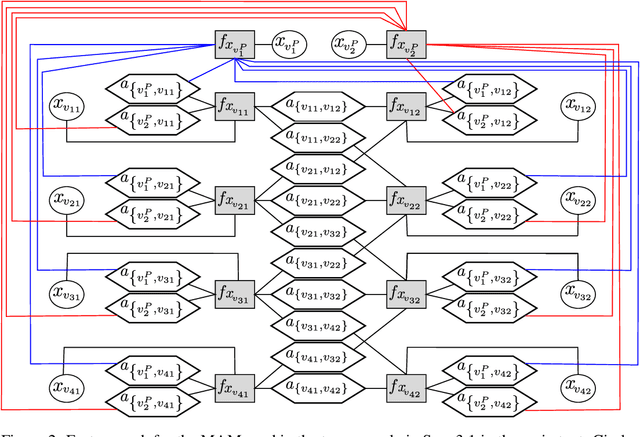
Discrete undirected graphical models, also known as Markov Random Fields (MRFs), can flexibly encode probabilistic interactions of multiple variables, and have enjoyed successful applications to a wide range of problems. However, a well-known yet little studied limitation of discrete MRFs is that they cannot capture context-specific independence (CSI). Existing methods require carefully developed theories and purpose-built inference methods, which limit their applications to only small-scale problems. In this paper, we propose the Markov Attention Model (MAM), a family of discrete MRFs that incorporates an attention mechanism. The attention mechanism allows variables to dynamically attend to some other variables while ignoring the rest, and enables capturing of CSIs in MRFs. A MAM is formulated as an MRF, allowing it to benefit from the rich set of existing MRF inference methods and scale to large models and datasets. To demonstrate MAM's capabilities to capture CSIs at scale, we apply MAMs to capture an important type of CSI that is present in a symbolic approach to recurrent computations in perceptual grouping. Experiments on two recently proposed synthetic perceptual grouping tasks and on realistic images demonstrate the advantages of MAMs in sample-efficiency, interpretability and generalizability when compared with strong recurrent neural network baselines, and validate MAM's capabilities to efficiently capture CSIs at scale.

Perturb-and-max-product: Sampling and learning in discrete energy-based models

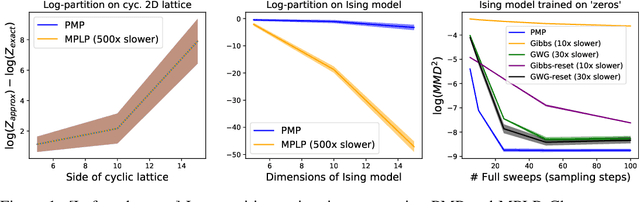
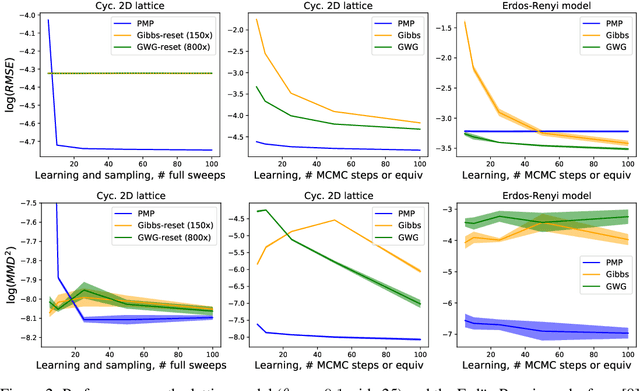
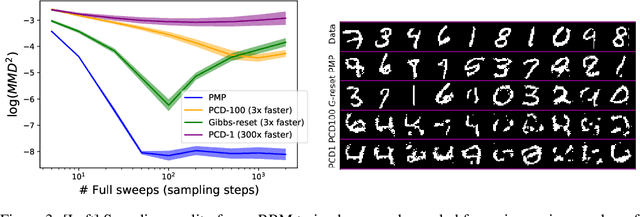
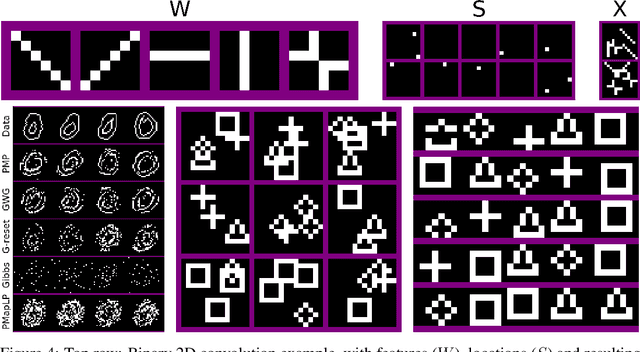
Perturb-and-MAP offers an elegant approach to approximately sample from a energy-based model (EBM) by computing the maximum-a-posteriori (MAP) configuration of a perturbed version of the model. Sampling in turn enables learning. However, this line of research has been hindered by the general intractability of the MAP computation. Very few works venture outside tractable models, and when they do, they use linear programming approaches, which as we will show, have several limitations. In this work we present perturb-and-max-product (PMP), a parallel and scalable mechanism for sampling and learning in discrete EBMs. Models can be arbitrary as long as they are built using tractable factors. We show that (a) for Ising models, PMP is orders of magnitude faster than Gibbs and Gibbs-with-Gradients (GWG) at learning and generating samples of similar or better quality; (b) PMP is able to learn and sample from RBMs; (c) in a large, entangled graphical model in which Gibbs and GWG fail to mix, PMP succeeds.

Sample-efficient L0-L2 constrained structure learning of sparse Ising models

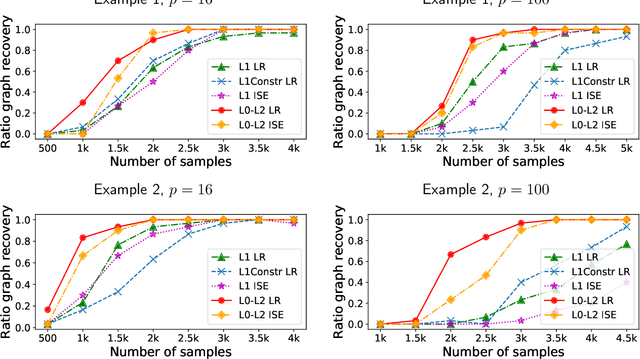
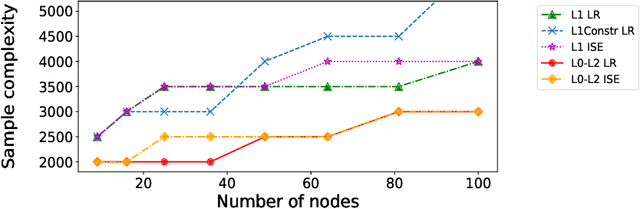
We consider the problem of learning the underlying graph of a sparse Ising model with $p$ nodes from $n$ i.i.d. samples. The most recent and best performing approaches combine an empirical loss (the logistic regression loss or the interaction screening loss) with a regularizer (an L1 penalty or an L1 constraint). This results in a convex problem that can be solved separately for each node of the graph. In this work, we leverage the cardinality constraint L0 norm, which is known to properly induce sparsity, and further combine it with an L2 norm to better model the non-zero coefficients. We show that our proposed estimators achieve an improved sample complexity, both (a) theoretically -- by reaching new state-of-the-art upper bounds for recovery guarantees -- and (b) empirically -- by showing sharper phase transitions between poor and full recovery for graph topologies studied in the literature -- when compared to their L1-based counterparts.

Query Training: Learning and inference for directed and undirected graphical models

Probabilistic graphical models (PGMs) provide a compact representation of knowledge that can be queried in a flexible way: after learning the parameters of a graphical model, new probabilistic queries can be answered at test time without retraining. However, learning undirected graphical models is notoriously hard due to the intractability of the partition function. For directed models, a popular approach is to use variational autoencoders, but there is no systematic way to choose the encoder architecture given the PGM, and the encoder only amortizes inference for a single probabilistic query (i.e., new queries require separate training). We introduce Query Training (QT), a systematic method to turn any PGM structure (directed or not, with or without hidden variables) into a trainable inference network. This single network can approximate any inference query. We demonstrate experimentally that QT can be used to learn a challenging 8-connected grid Markov random field with hidden variables and that it consistently outperforms the state-of-the-art AdVIL when tested on three undirected models across multiple datasets.

Learning Sparse Classifiers: Continuous and Mixed Integer Optimization Perspectives

We consider a discrete optimization based approach for learning sparse classifiers, where the outcome depends upon a linear combination of a small subset of features. Recent work has shown that mixed integer programming (MIP) can be used to solve (to optimality) $\ell_0$-regularized problems at scales much larger than what was conventionally considered possible in the statistics and machine learning communities. Despite their usefulness, MIP-based approaches are significantly slower compared to relatively mature algorithms based on $\ell_1$-regularization and relatives. We aim to bridge this computational gap by developing new MIP-based algorithms for $\ell_0$-regularized classification. We propose two classes of scalable algorithms: an exact algorithm that can handle $p\approx 50,000$ features in a few minutes, and approximate algorithms that can address instances with $p\approx 10^6$ in times comparable to fast $\ell_1$-based algorithms. Our exact algorithm is based on the novel idea of \textsl{integrality generation}, which solves the original problem (with $p$ binary variables) via a sequence of mixed integer programs that involve a small number of binary variables. Our approximate algorithms are based on coordinate descent and local combinatorial search. In addition, we present new estimation error bounds for a class of $\ell_0$-regularized estimators. Experiments on real and synthetic data demonstrate that our approach leads to models with considerably improved statistical performance (especially, variable selection) when compared to competing toolkits.