Towards Spectroscopy: Susceptibility Clusters in Language Models

Spectroscopy infers the internal structure of physical systems by measuring their response to perturbations. We apply this principle to neural networks: perturbing the data distribution by upweighting a token $y$ in context $x$, we measure the model's response via susceptibilities $χ_{xy}$, which are covariances between component-level observables and the perturbation computed over a localized Gibbs posterior via stochastic gradient Langevin dynamics (SGLD). Theoretically, we show that susceptibilities decompose as a sum over modes of the data distribution, explaining why tokens that follow their contexts "for similar reasons" cluster together in susceptibility space. Empirically, we apply this methodology to Pythia-14M, developing a conductance-based clustering algorithm that identifies 510 interpretable clusters ranging from grammatical patterns to code structure to mathematical notation. Comparing to sparse autoencoders, 50% of our clusters match SAE features, validating that both methods recover similar structure.

SCALAR: Benchmarking SAE Interaction Sparsity in Toy LLMs

Mechanistic interpretability aims to decompose neural networks into interpretable features and map their connecting circuits. The standard approach trains sparse autoencoders (SAEs) on each layer's activations. However, SAEs trained in isolation don't encourage sparse cross-layer connections, inflating extracted circuits where upstream features needlessly affect multiple downstream features. Current evaluations focus on individual SAE performance, leaving interaction sparsity unexamined. We introduce SCALAR (Sparse Connectivity Assessment of Latent Activation Relationships), a benchmark measuring interaction sparsity between SAE features. We also propose "Staircase SAEs", using weight-sharing to limit upstream feature duplication across downstream features. Using SCALAR, we compare TopK SAEs, Jacobian SAEs (JSAEs), and Staircase SAEs. Staircase SAEs improve relative sparsity over TopK SAEs by $59.67\% \pm 1.83\%$ (feedforward) and $63.15\% \pm 1.35\%$ (transformer blocks). JSAEs provide $8.54\% \pm 0.38\%$ improvement over TopK for feedforward layers but cannot train effectively across transformer blocks, unlike Staircase and TopK SAEs which work anywhere in the residual stream. We validate on a $216$K-parameter toy model and GPT-$2$ Small ($124$M), where Staircase SAEs maintain interaction sparsity improvements while preserving feature interpretability. Our work highlights the importance of interaction sparsity in SAEs through benchmarking and comparing promising architectures.

Embryology of a Language Model

Understanding how language models develop their internal computational structure is a central problem in the science of deep learning. While susceptibilities, drawn from statistical physics, offer a promising analytical tool, their full potential for visualizing network organization remains untapped. In this work, we introduce an embryological approach, applying UMAP to the susceptibility matrix to visualize the model's structural development over training. Our visualizations reveal the emergence of a clear ``body plan,'' charting the formation of known features like the induction circuit and discovering previously unknown structures, such as a ``spacing fin'' dedicated to counting space tokens. This work demonstrates that susceptibility analysis can move beyond validation to uncover novel mechanisms, providing a powerful, holistic lens for studying the developmental principles of complex neural networks.

Prevalence and prevention of large language model use in crowd work

We show that the use of large language models (LLMs) is prevalent among crowd workers, and that targeted mitigation strategies can significantly reduce, but not eliminate, LLM use. On a text summarization task where workers were not directed in any way regarding their LLM use, the estimated prevalence of LLM use was around 30%, but was reduced by about half by asking workers to not use LLMs and by raising the cost of using them, e.g., by disabling copy-pasting. Secondary analyses give further insight into LLM use and its prevention: LLM use yields high-quality but homogeneous responses, which may harm research concerned with human (rather than model) behavior and degrade future models trained with crowdsourced data. At the same time, preventing LLM use may be at odds with obtaining high-quality responses; e.g., when requesting workers not to use LLMs, summaries contained fewer keywords carrying essential information. Our estimates will likely change as LLMs increase in popularity or capabilities, and as norms around their usage change. Yet, understanding the co-evolution of LLM-based tools and users is key to maintaining the validity of research done using crowdsourcing, and we provide a critical baseline before widespread adoption ensues.

Rows from Many Sources: Enriching row completions from Wikidata with a pre-trained Language Model

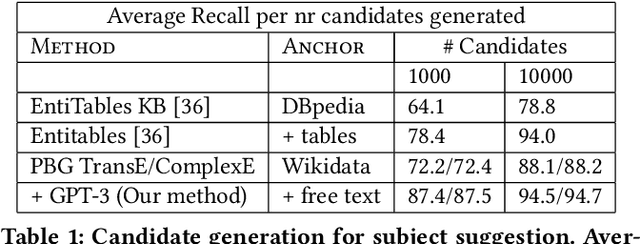
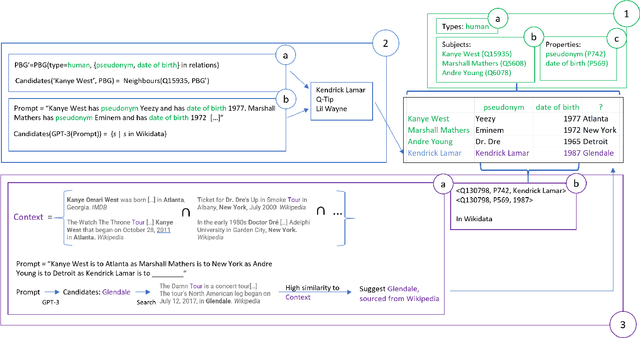
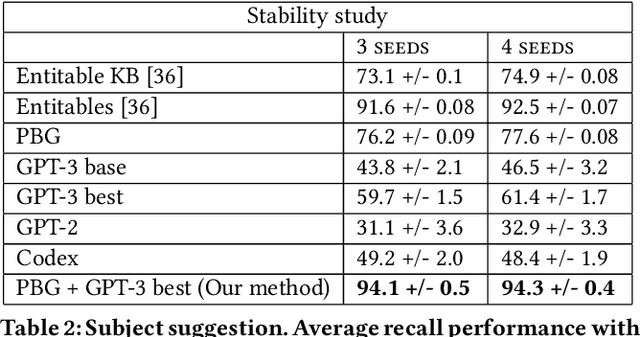
Row completion is the task of augmenting a given table of text and numbers with additional, relevant rows. The task divides into two steps: subject suggestion, the task of populating the main column; and gap filling, the task of populating the remaining columns. We present state-of-the-art results for subject suggestion and gap filling measured on a standard benchmark (WikiTables). Our idea is to solve this task by harmoniously combining knowledge base table interpretation and free text generation. We interpret the table using the knowledge base to suggest new rows and generate metadata like headers through property linking. To improve candidate diversity, we synthesize additional rows using free text generation via GPT-3, and crucially, we exploit the metadata we interpret to produce better prompts for text generation. Finally, we verify that the additional synthesized content can be linked to the knowledge base or a trusted web source such as Wikipedia.

The Wreath Process: A totally generative model of geometric shape based on nested symmetries

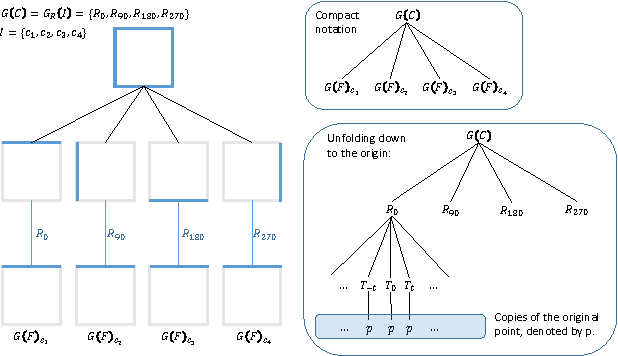
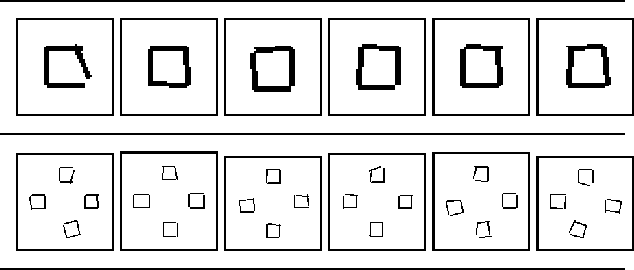
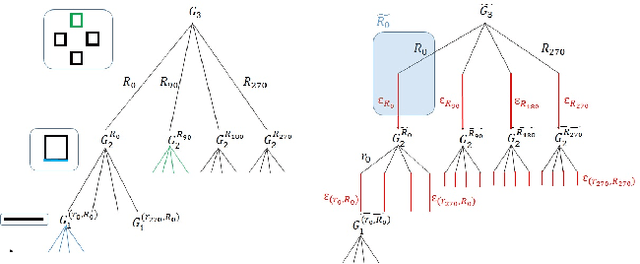
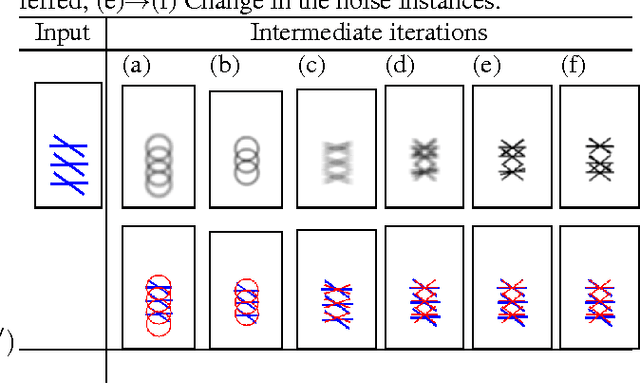
We consider the problem of modelling noisy but highly symmetric shapes that can be viewed as hierarchies of whole-part relationships in which higher level objects are composed of transformed collections of lower level objects. To this end, we propose the stochastic wreath process, a fully generative probabilistic model of drawings. Following Leyton's "Generative Theory of Shape", we represent shapes as sequences of transformation groups composed through a wreath product. This representation emphasizes the maximization of transfer --- the idea that the most compact and meaningful representation of a given shape is achieved by maximizing the re-use of existing building blocks or parts. The proposed stochastic wreath process extends Leyton's theory by defining a probability distribution over geometric shapes in terms of noise processes that are aligned with the generative group structure of the shape. We propose an inference scheme for recovering the generative history of given images in terms of the wreath process using reversible jump Markov chain Monte Carlo methods and Approximate Bayesian Computation. In the context of sketching we demonstrate the feasibility and limitations of this approach on model-generated and real data.