Ali H. Sayed
Second-Order Guarantees of Stochastic Gradient Descent in Non-Convex Optimization
Aug 19, 2019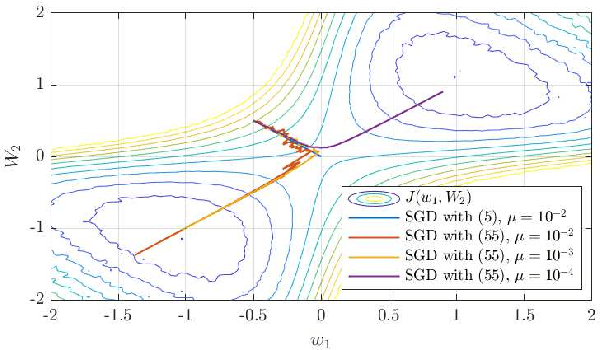
Abstract:Recent years have seen increased interest in performance guarantees of gradient descent algorithms for non-convex optimization. A number of works have uncovered that gradient noise plays a critical role in the ability of gradient descent recursions to efficiently escape saddle-points and reach second-order stationary points. Most available works limit the gradient noise component to be bounded with probability one or sub-Gaussian and leverage concentration inequalities to arrive at high-probability results. We present an alternate approach, relying primarily on mean-square arguments and show that a more relaxed relative bound on the gradient noise variance is sufficient to ensure efficient escape from saddle-points without the need to inject additional noise, employ alternating step-sizes or rely on a global dispersive noise assumption, as long as a gradient noise component is present in a descent direction for every saddle-point.
Distributed Learning in Non-Convex Environments -- Part II: Polynomial Escape from Saddle-Points
Jul 03, 2019
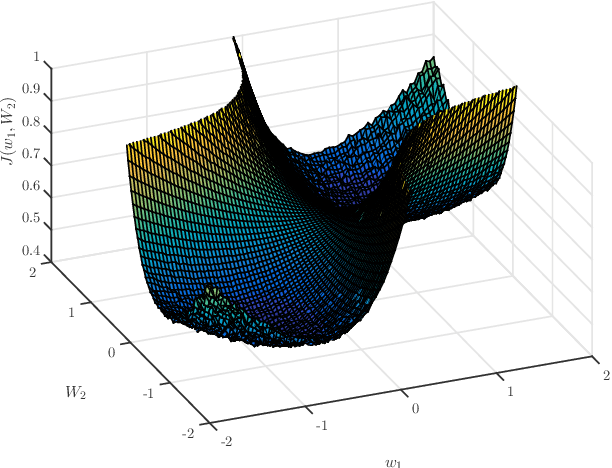
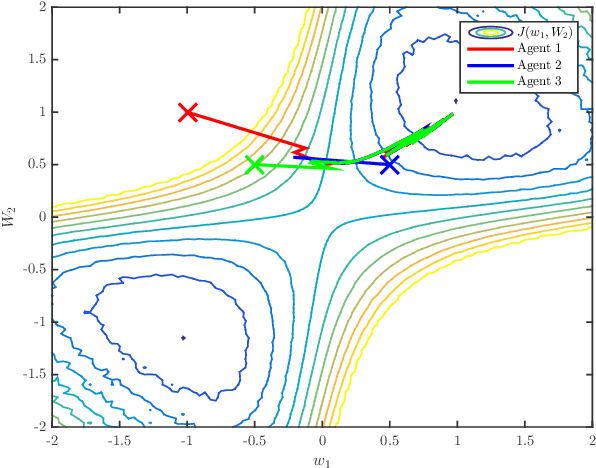
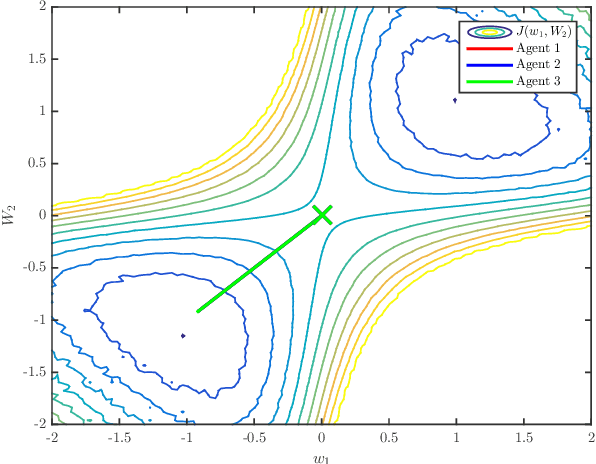
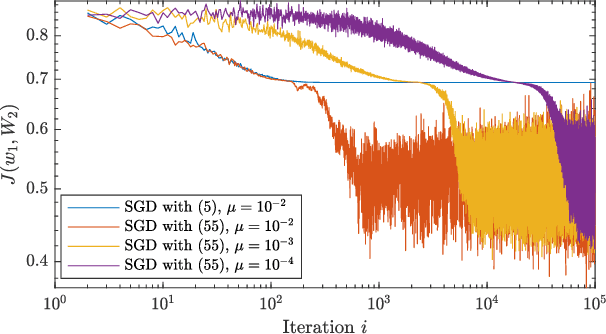
Abstract:The diffusion strategy for distributed learning from streaming data employs local stochastic gradient updates along with exchange of iterates over neighborhoods. In Part I [2] of this work we established that agents cluster around a network centroid and proceeded to study the dynamics of this point. We established expected descent in non-convex environments in the large-gradient regime and introduced a short-term model to examine the dynamics over finite-time horizons. Using this model, we establish in this work that the diffusion strategy is able to escape from strict saddle-points in O(1/$\mu$) iterations; it is also able to return approximately second-order stationary points in a polynomial number of iterations. Relative to prior works on the polynomial escape from saddle-points, most of which focus on centralized perturbed or stochastic gradient descent, our approach requires less restrictive conditions on the gradient noise process.
Learning Erdős-Rényi Graphs under Partial Observations: Concentration or Sparsity?
Apr 05, 2019
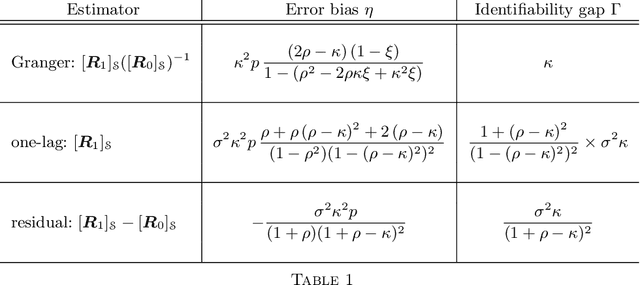
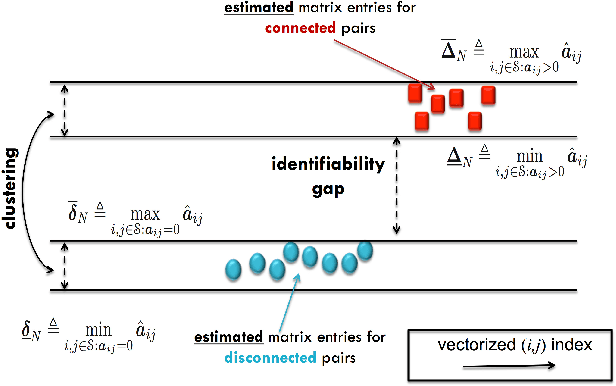

Abstract:This work examines the problem of graph learning over a diffusion network when data can be collected from a limited portion of the network (partial observability). While most works in the literature rely on a degree of sparsity to provide guarantees of consistent graph recovery, our analysis moves away from this condition and includes the demanding setting of dense connectivity. We ascertain that suitable estimators of the combination matrix (i.e., the matrix that quantifies the pairwise interaction between nodes) possess an identifiability gap that enables the discrimination between connected and disconnected nodes. Fundamental conditions are established under which the subgraph of monitored nodes can be recovered, with high probability as the network size increases, through universal clustering algorithms. This claim is proved for three matrix estimators: i) the Granger estimator that adapts to the partial observability setting the solution that is optimal under full observability ; ii) the one-lag correlation matrix; and iii) the residual estimator based on the difference between two consecutive time samples. Comparison among the estimators is performed through illustrative examples that reveal how estimators that are not optimal in the full observability regime can outperform the Granger estimator in the partial observability regime. The analysis reveals that the fundamental property enabling consistent graph learning is the statistical concentration of node degrees, rather than the sparsity of connections.
On the Performance of Exact Diffusion over Adaptive Networks
Mar 26, 2019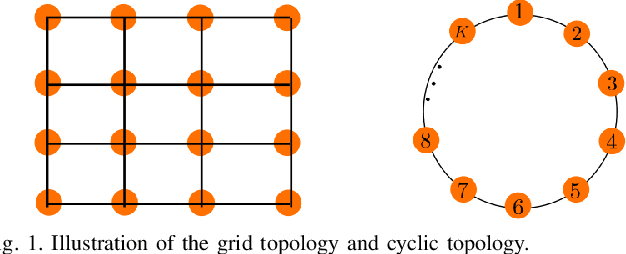
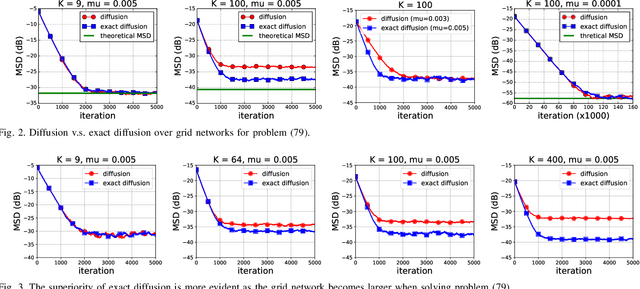
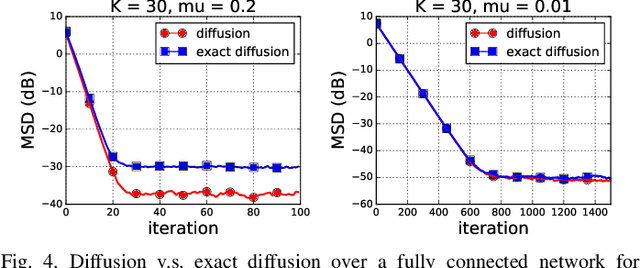
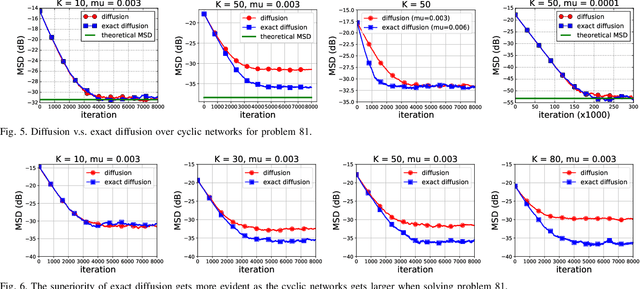
Abstract:Various bias-correction methods such as EXTRA, DIGing, and exact diffusion have been proposed recently to solve distributed deterministic optimization problems. These methods employ constant step-sizes and converge linearly to the {\em exact} solution under proper conditions. However, their performance under stochastic and adaptive settings remains unclear. It is still unknown whether the bias-correction is necessary over adaptive networks. By studying exact diffusion and examining its steady-state performance under stochastic scenarios, this paper provides affirmative results. It is shown that the correction step in exact diffusion leads to better steady-state performance than traditional methods. It is also analytically shown the superiority of exact diffusion is more evident over badly-connected network topologies.
Decentralized Decision-Making Over Multi-Task Networks
Dec 24, 2018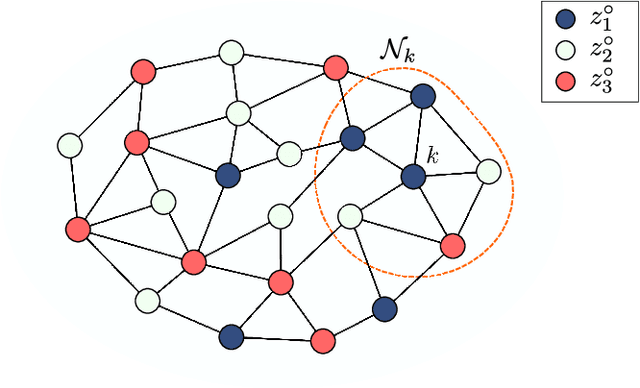

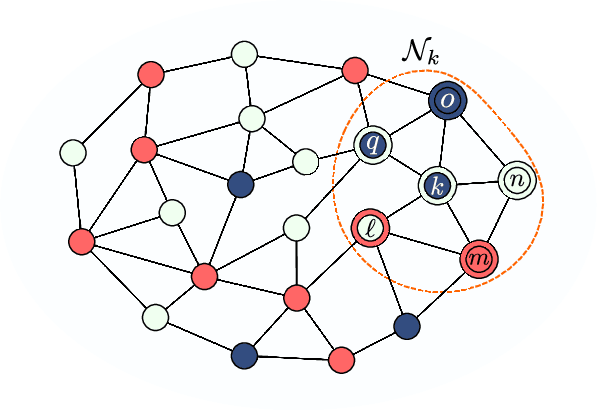
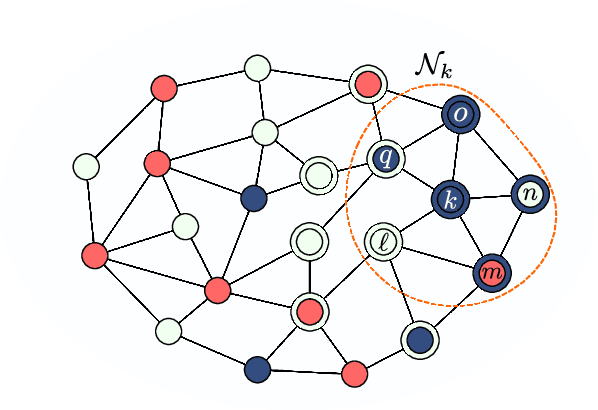
Abstract:In important applications involving multi-task networks with multiple objectives, agents in the network need to decide between these multiple objectives and reach an agreement about which single objective to follow for the network. In this work we propose a distributed decision-making algorithm. The agents are assumed to observe data that may be generated by different models. Through localized interactions, the agents reach agreement about which model to track and interact with each other in order to enhance the network performance. We investigate the approach for both static and mobile networks. The simulations illustrate the performance of the proposed strategies.
Multi-Agent Fully Decentralized Off-Policy Learning with Linear Convergence Rates
Oct 17, 2018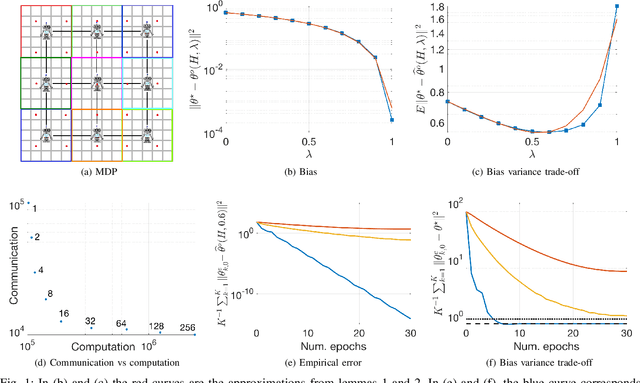
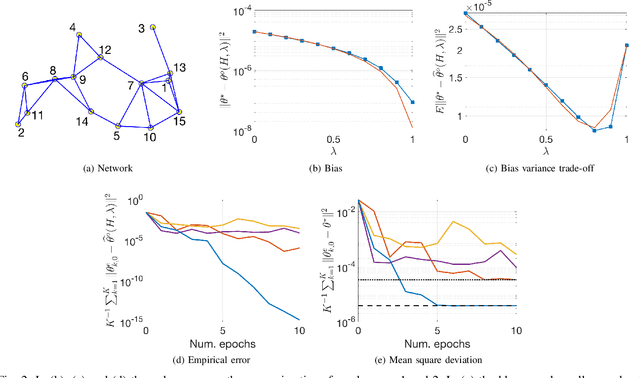
Abstract:In this paper we develop a fully decentralized algorithm for policy evaluation with off-policy learning, linear function approximation, and $O(n)$ complexity in both computation and memory requirements. The proposed algorithm is of the variance reduced kind and achieves linear convergence. We consider the case where a collection of agents have distinct and fixed size datasets gathered following different behavior policies (none of which is required to explore the full state space) and they all collaborate to evaluate a common target policy. The network approach allows all agents to converge to the optimal solution even in situations where neither agent can converge on its own without cooperation. We provide simulations to illustrate the effectiveness of the method.
Stochastic Learning under Random Reshuffling with Constant Step-sizes
Oct 09, 2018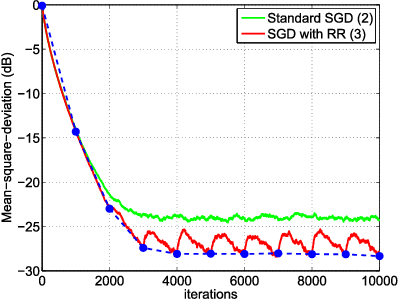
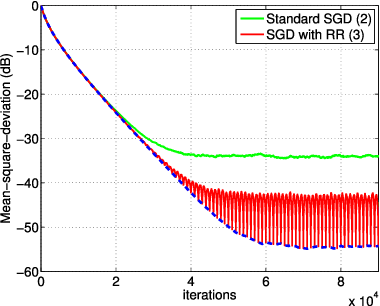
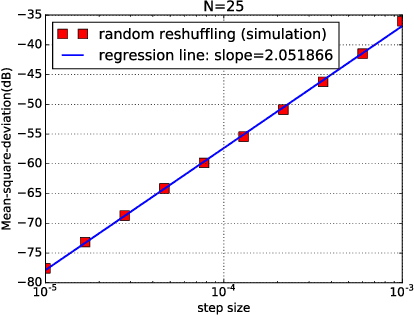
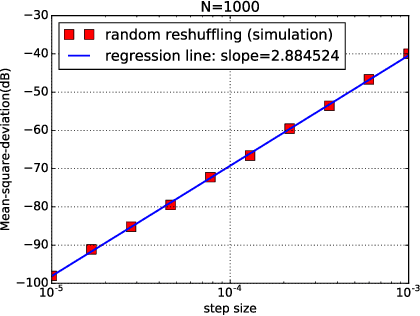
Abstract:In empirical risk optimization, it has been observed that stochastic gradient implementations that rely on random reshuffling of the data achieve better performance than implementations that rely on sampling the data uniformly. Recent works have pursued justifications for this behavior by examining the convergence rate of the learning process under diminishing step-sizes. This work focuses on the constant step-size case and strongly convex loss function. In this case, convergence is guaranteed to a small neighborhood of the optimizer albeit at a linear rate. The analysis establishes analytically that random reshuffling outperforms uniform sampling by showing explicitly that iterates approach a smaller neighborhood of size $O(\mu^2)$ around the minimizer rather than $O(\mu)$. Furthermore, we derive an analytical expression for the steady-state mean-square-error performance of the algorithm, which helps clarify in greater detail the differences between sampling with and without replacement. We also explain the periodic behavior that is observed in random reshuffling implementations.
Learning Kolmogorov Models for Binary Random Variables
Jun 06, 2018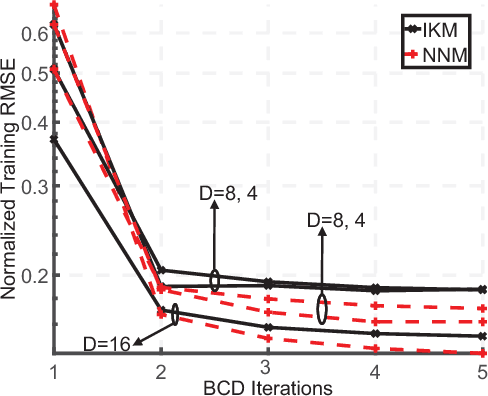

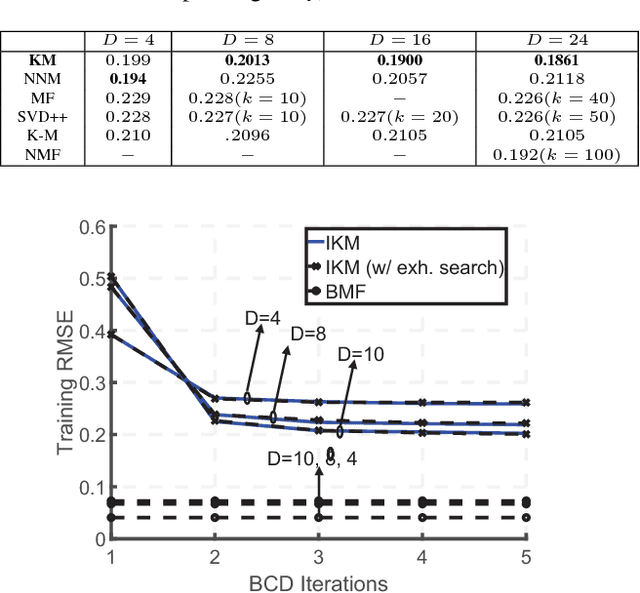
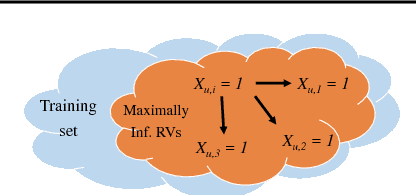
Abstract:We summarize our recent findings, where we proposed a framework for learning a Kolmogorov model, for a collection of binary random variables. More specifically, we derive conditions that link outcomes of specific random variables, and extract valuable relations from the data. We also propose an algorithm for computing the model and show its first-order optimality, despite the combinatorial nature of the learning problem. We apply the proposed algorithm to recommendation systems, although it is applicable to other scenarios. We believe that the work is a significant step toward interpretable machine learning.
Variance-Reduced Stochastic Learning by Networked Agents under Random Reshuffling
May 29, 2018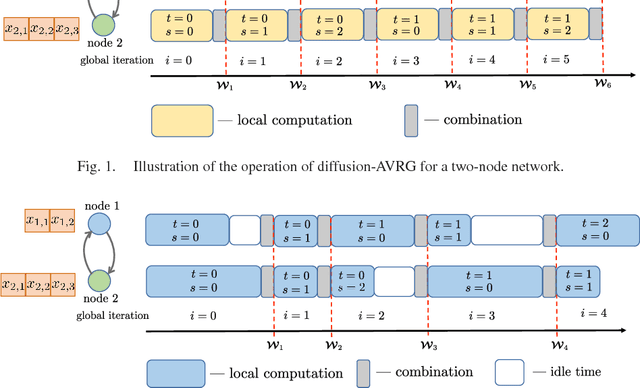

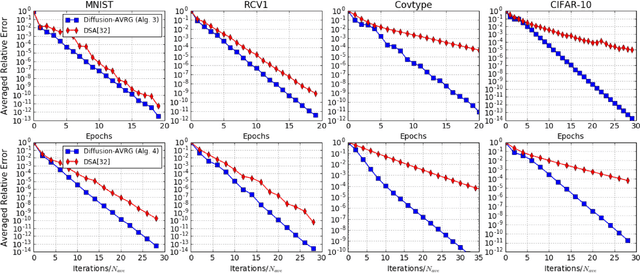
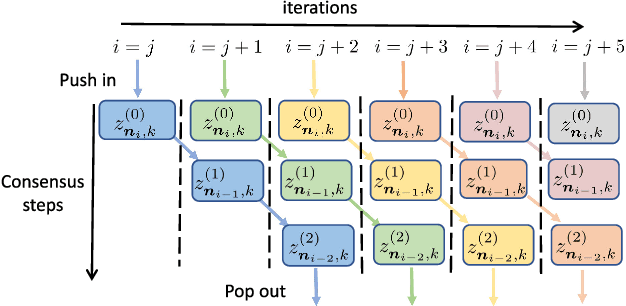
Abstract:A new amortized variance-reduced gradient (AVRG) algorithm was developed in \cite{ying2017convergence}, which has constant storage requirement in comparison to SAGA and balanced gradient computations in comparison to SVRG. One key advantage of the AVRG strategy is its amenability to decentralized implementations. In this work, we show how AVRG can be extended to the network case where multiple learning agents are assumed to be connected by a graph topology. In this scenario, each agent observes data that is spatially distributed and all agents are only allowed to communicate with direct neighbors. Moreover, the amount of data observed by the individual agents may differ drastically. For such situations, the balanced gradient computation property of AVRG becomes a real advantage in reducing idle time caused by unbalanced local data storage requirements, which is characteristic of other reduced-variance gradient algorithms. The resulting diffusion-AVRG algorithm is shown to have linear convergence to the exact solution, and is much more memory efficient than other alternative algorithms. In addition, we propose a mini-batch strategy to balance the communication and computation efficiency for diffusion-AVRG. When a proper batch size is employed, it is observed in simulations that diffusion-AVRG is more computationally efficient than exact diffusion or EXTRA while maintaining almost the same communication efficiency.
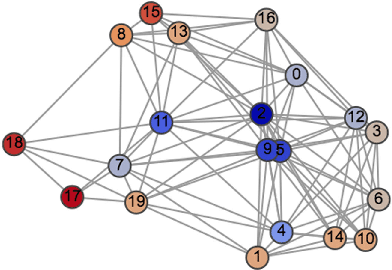
Learning Under Distributed Features
May 29, 2018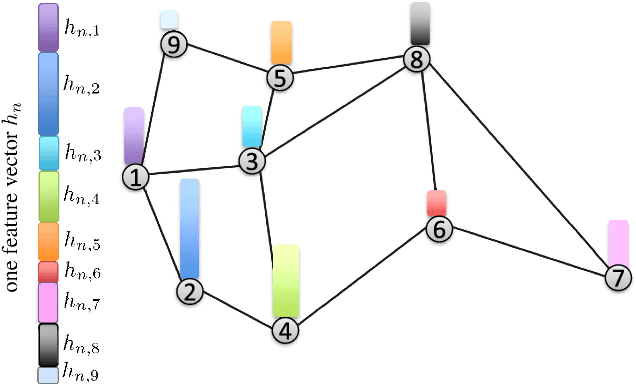
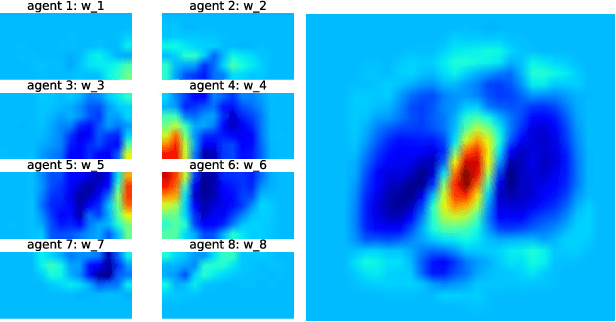
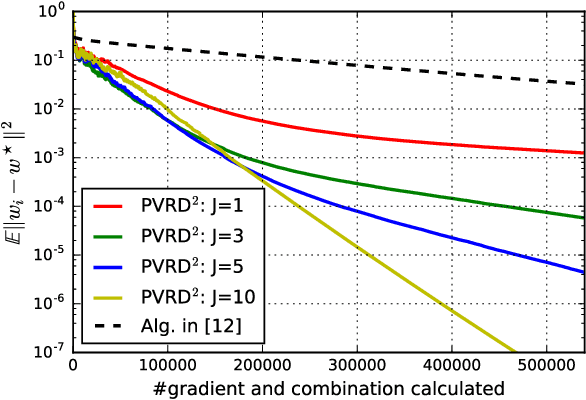
Abstract:This work studies the problem of learning under both large data and large feature space scenarios. The feature information is assumed to be spread across agents in a network, where each agent observes some of the features. Through local cooperation, the agents are supposed to interact with each other to solve the inference problem and converge towards the global minimizer of the empirical risk. We study this problem exclusively in the primal domain, and propose new and effective distributed solutions with guaranteed convergence to the minimizer. This is achieved by combining a dynamic diffusion construction, a pipeline strategy, and variance-reduced techniques. Simulation results illustrate the conclusions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge