Doubly Adaptive Social Learning

In social learning, a network of agents assigns probability scores (beliefs) to some hypotheses of interest, which rule the generation of local streaming data observed by each agent. Belief formation takes place by means of an iterative two-step procedure where: i) the agents update locally their beliefs by using some likelihood model; and ii) the updated beliefs are combined with the beliefs of the neighboring agents, using a pooling rule. This procedure can fail to perform well in the presence of dynamic drifts, leading the agents to incorrect decision making. Here, we focus on the fully online setting where both the true hypothesis and the likelihood models can change over time. We propose the doubly adaptive social learning ($\text{A}^2\text{SL}$) strategy, which infuses social learning with the necessary adaptation capabilities. This goal is achieved by exploiting two adaptation stages: i) a stochastic gradient descent update to learn and track the drifts in the decision model; ii) and an adaptive belief update to track the true hypothesis changing over time. These stages are controlled by two adaptation parameters that govern the evolution of the error probability for each agent. We show that all agents learn consistently for sufficiently small adaptation parameters, in the sense that they ultimately place all their belief mass on the true hypothesis. In particular, the probability of choosing the wrong hypothesis converges to values on the order of the adaptation parameters. The theoretical analysis is illustrated both on synthetic data and by applying the $\text{A}^2\text{SL}$ strategy to a social learning problem in the online setting using real data.

Differential error feedback for communication-efficient decentralized learning

Communication-constrained algorithms for decentralized learning and optimization rely on local updates coupled with the exchange of compressed signals. In this context, differential quantization is an effective technique to mitigate the negative impact of compression by leveraging correlations between successive iterates. In addition, the use of error feedback, which consists of incorporating the compression error into subsequent steps, is a powerful mechanism to compensate for the bias caused by the compression. Under error feedback, performance guarantees in the literature have so far focused on algorithms employing a fusion center or a special class of contractive compressors that cannot be implemented with a finite number of bits. In this work, we propose a new decentralized communication-efficient learning approach that blends differential quantization with error feedback. The approach is specifically tailored for decentralized learning problems where agents have individual risk functions to minimize subject to subspace constraints that require the minimizers across the network to lie in low-dimensional subspaces. This constrained formulation includes consensus or single-task optimization as special cases, and allows for more general task relatedness models such as multitask smoothness and coupled optimization. We show that, under some general conditions on the compression noise, and for sufficiently small step-sizes $\mu$, the resulting communication-efficient strategy is stable both in terms of mean-square error and average bit rate: by reducing $\mu$, it is possible to keep the estimation errors small (on the order of $\mu$) without increasing indefinitely the bit rate as $\mu\rightarrow 0$. The results establish that, in the small step-size regime and with a finite number of bits, it is possible to attain the performance achievable in the absence of compression.

Compressed Regression over Adaptive Networks

In this work we derive the performance achievable by a network of distributed agents that solve, adaptively and in the presence of communication constraints, a regression problem. Agents employ the recently proposed ACTC (adapt-compress-then-combine) diffusion strategy, where the signals exchanged locally by neighboring agents are encoded with randomized differential compression operators. We provide a detailed characterization of the mean-square estimation error, which is shown to comprise a term related to the error that agents would achieve without communication constraints, plus a term arising from compression. The analysis reveals quantitative relationships between the compression loss and fundamental attributes of the distributed regression problem, in particular, the stochastic approximation error caused by the gradient noise and the network topology (through the Perron eigenvector). We show that knowledge of such relationships is critical to allocate optimally the communication resources across the agents, taking into account their individual attributes, such as the quality of their data or their degree of centrality in the network topology. We devise an optimized allocation strategy where the parameters necessary for the optimization can be learned online by the agents. Illustrative examples show that a significant performance improvement, as compared to a blind (i.e., uniform) resource allocation, can be achieved by optimizing the allocation by means of the provided mean-square-error formulas.

Memory-Aware Social Learning under Partial Information Sharing

This work examines a social learning problem, where dispersed agents connected through a network topology interact locally to form their opinions (beliefs) as regards certain hypotheses of interest. These opinions evolve over time, since the agents collect observations from the environment, and update their current beliefs by accounting for: their past beliefs, the innovation contained in the new data, and the beliefs received from the neighbors. The distinguishing feature of the present work is that agents are constrained to share opinions regarding only a single hypothesis. We devise a novel learning strategy where each agent forms a valid belief by completing the partial beliefs received from its neighbors. This completion is performed by exploiting the knowledge accumulated in the past beliefs, thanks to a principled memory-aware rule inspired by a Bayesian criterion. The analysis allows us to characterize the role of memory in social learning under partial information sharing, revealing novel and nontrivial learning dynamics. Surprisingly, we establish that the standard classification rule based on selecting the maximum belief is not optimal under partial information sharing, while there exists a consistent threshold-based decision rule that allows each agent to classify correctly the hypothesis of interest. We also show that the proposed strategy outperforms previously considered schemes, highlighting that the introduction of memory in the social learning algorithm is critical to overcome the limitations arising from sharing partial information.

Distributed Bayesian Learning of Dynamic States

This work studies networked agents cooperating to track a dynamical state of nature under partial information. The proposed algorithm is a distributed Bayesian filtering algorithm for finite-state hidden Markov models (HMMs). It can be used for sequential state estimation tasks, as well as for modeling opinion formation over social networks under dynamic environments. We show that the disagreement with the optimal centralized solution is asymptotically bounded for the class of geometrically ergodic state transition models, which includes rapidly changing models. We also derive recursions for calculating the probability of error and establish convergence under Gaussian observation models. Simulations are provided to illustrate the theory and to compare against alternative approaches.

Quantization for decentralized learning under subspace constraints

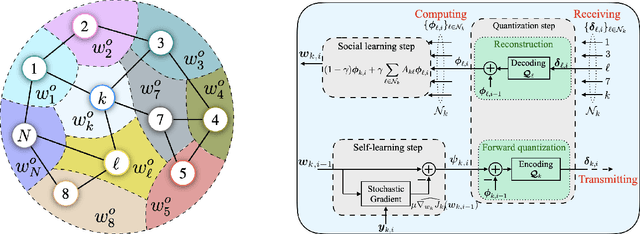
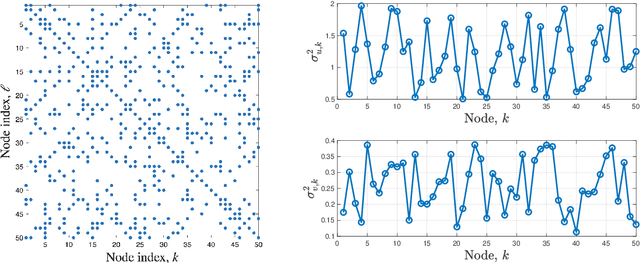
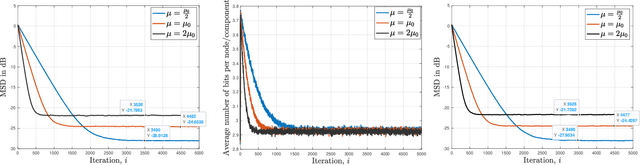
In this paper, we consider decentralized optimization problems where agents have individual cost functions to minimize subject to subspace constraints that require the minimizers across the network to lie in low-dimensional subspaces. This constrained formulation includes consensus or single-task optimization as special cases, and allows for more general task relatedness models such as multitask smoothness and coupled optimization. In order to cope with communication constraints, we propose and study an adaptive decentralized strategy where the agents employ differential randomized quantizers to compress their estimates before communicating with their neighbors. The analysis shows that, under some general conditions on the quantization noise, and for sufficiently small step-sizes $\mu$, the strategy is stable both in terms of mean-square error and average bit rate: by reducing $\mu$, it is possible to keep the estimation errors small (on the order of $\mu$) without increasing indefinitely the bit rate as $\mu\rightarrow 0$. Simulations illustrate the theoretical findings and the effectiveness of the proposed approach, revealing that decentralized learning is achievable at the expense of only a few bits.

Learning from Heterogeneous Data Based on Social Interactions over Graphs

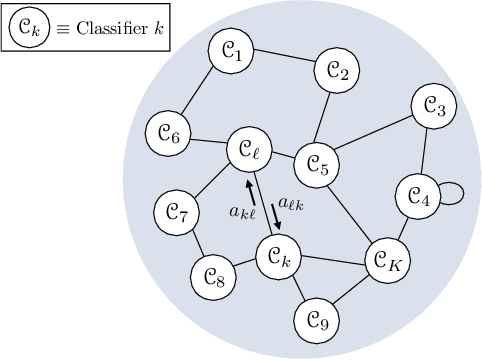
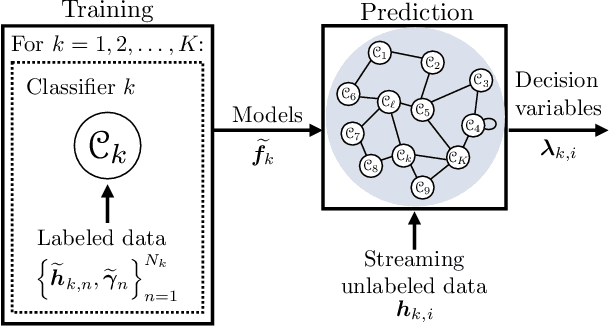
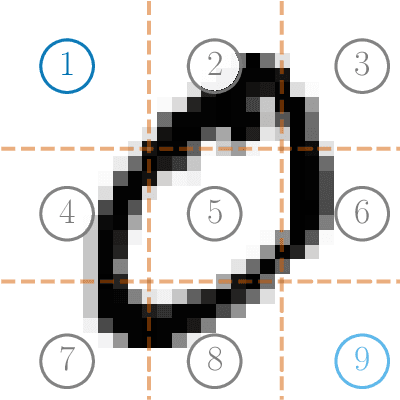
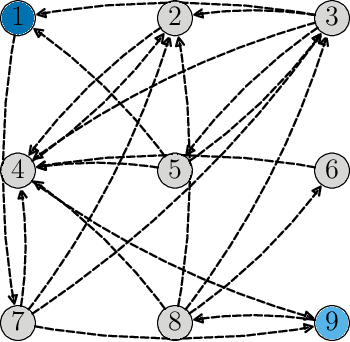
This work proposes a decentralized architecture, where individual agents aim at solving a classification problem while observing streaming features of different dimensions and arising from possibly different distributions. In the context of social learning, several useful strategies have been developed, which solve decision making problems through local cooperation across distributed agents and allow them to learn from streaming data. However, traditional social learning strategies rely on the fundamental assumption that each agent has significant prior knowledge of the underlying distribution of the observations. In this work we overcome this issue by introducing a machine learning framework that exploits social interactions over a graph, leading to a fully data-driven solution to the distributed classification problem. In the proposed social machine learning (SML) strategy, two phases are present: in the training phase, classifiers are independently trained to generate a belief over a set of hypotheses using a finite number of training samples; in the prediction phase, classifiers evaluate streaming unlabeled observations and share their instantaneous beliefs with neighboring classifiers. We show that the SML strategy enables the agents to learn consistently under this highly-heterogeneous setting and allows the network to continue learning even during the prediction phase when it is deciding on unlabeled samples. The prediction decisions are used to continually improve performance thereafter in a manner that is markedly different from most existing static classification schemes where, following training, the decisions on unlabeled data are not re-used to improve future performance.

Distributed Adaptive Learning Under Communication Constraints

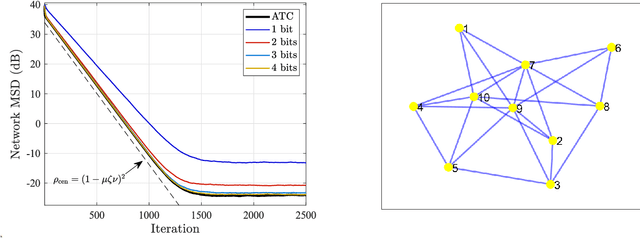
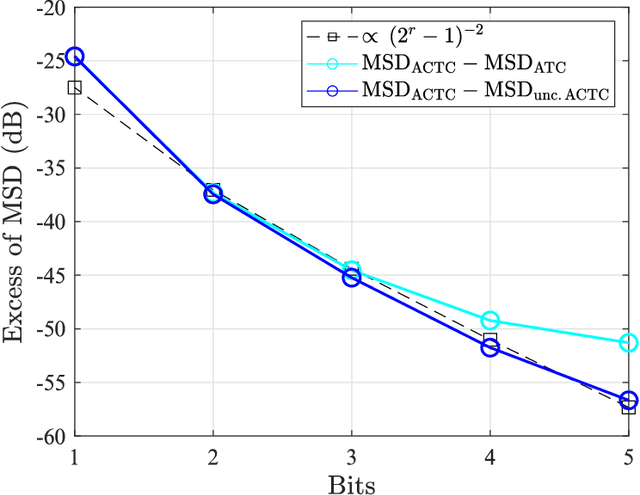
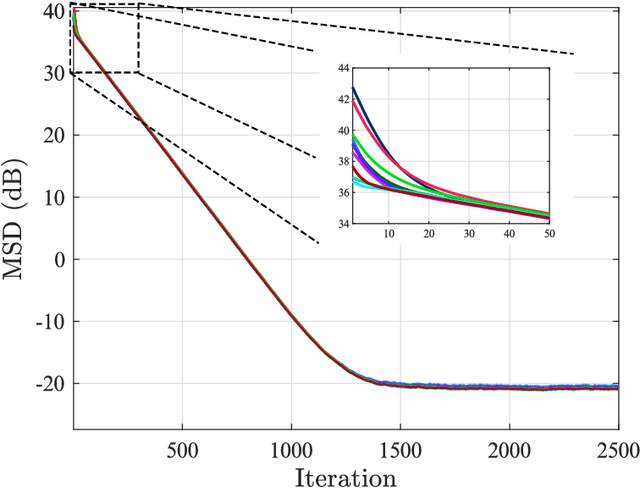
This work examines adaptive distributed learning strategies designed to operate under communication constraints. We consider a network of agents that must solve an online optimization problem from continual observation of streaming data. The agents implement a distributed cooperative strategy where each agent is allowed to perform local exchange of information with its neighbors. In order to cope with communication constraints, the exchanged information must be unavoidably compressed. We propose a diffusion strategy nicknamed as ACTC (Adapt-Compress-Then-Combine), which relies on the following steps: i) an adaptation step where each agent performs an individual stochastic-gradient update with constant step-size; ii) a compression step that leverages a recently introduced class of stochastic compression operators; and iii) a combination step where each agent combines the compressed updates received from its neighbors. The distinguishing elements of this work are as follows. First, we focus on adaptive strategies, where constant (as opposed to diminishing) step-sizes are critical to respond in real time to nonstationary variations. Second, we consider the general class of directed graphs and left-stochastic combination policies, which allow us to enhance the interplay between topology and learning. Third, in contrast with related works that assume strong convexity for all individual agents' cost functions, we require strong convexity only at a network level, a condition satisfied even if a single agent has a strongly-convex cost and the remaining agents have non-convex costs. Fourth, we focus on a diffusion (as opposed to consensus) strategy. Under the demanding setting of compressed information, we establish that the ACTC iterates fluctuate around the desired optimizer, achieving remarkable savings in terms of bits exchanged between neighboring agents.

Network Classifiers Based on Social Learning

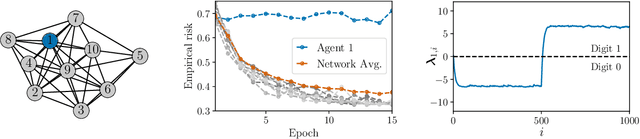
This work proposes a new way of combining independently trained classifiers over space and time. Combination over space means that the outputs of spatially distributed classifiers are aggregated. Combination over time means that the classifiers respond to streaming data during testing and continue to improve their performance even during this phase. By doing so, the proposed architecture is able to improve prediction performance over time with unlabeled data. Inspired by social learning algorithms, which require prior knowledge of the observations distribution, we propose a Social Machine Learning (SML) paradigm that is able to exploit the imperfect models generated during the learning phase. We show that this strategy results in consistent learning with high probability, and it yields a robust structure against poorly trained classifiers. Simulations with an ensemble of feedforward neural networks are provided to illustrate the theoretical results.

Inverse Graph Learning over Optimization Networks

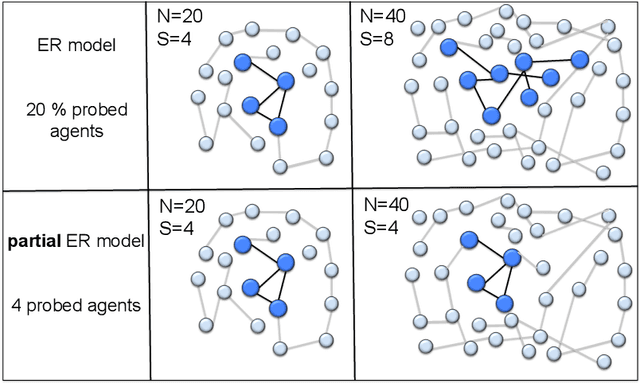
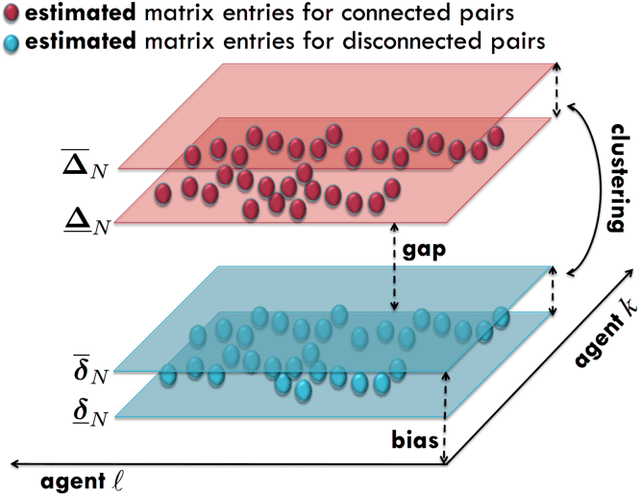
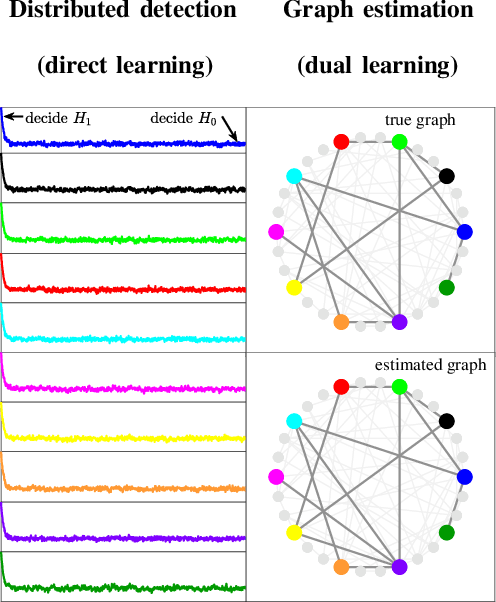
Many inferential and learning tasks can be accomplished efficiently by means of distributed optimization algorithms where the network topology plays a critical role in driving the local interactions among neighboring agents. There is a large body of literature examining the effect of the graph structure on the performance of optimization strategies. In this article, we examine the inverse problem and consider the reverse question: How much information does observing the behavior at the nodes convey about the underlying network structure used for optimization? Over large-scale networks, the difficulty of addressing such inverse questions (or problems) is compounded by the fact that usually only a limited portion of nodes can be probed, giving rise to a second important question: Despite the presence of several unobserved nodes, are partial and local observations still sufficient to discover the graph linking the probed nodes? The article surveys recent advances on this inverse learning problem and related questions. Examples of applications are provided to illustrate how the interplay between graph learning and distributed optimization arises in practice, e.g., in cognitive engineered systems such as distributed detection, or in other real-world problems such as the mechanism of opinion formation over social networks and the mechanism of coordination in biological networks. A unifying framework for examining the reconstruction error will be described, which allows to devise and examine various estimation strategies enabling successful graph learning. The relevance of specific network attributes, such as sparsity versus density of connections, and node degree concentration, is discussed in relation to the topology inference goal. It is shown how universal (i.e., data-driven) clustering algorithms can be exploited to solve the graph learning problem.