Straightness of Rectified Flow: A Theoretical Insight into Wasserstein Convergence

Diffusion models have emerged as a powerful tool for image generation and denoising. Typically, generative models learn a trajectory between the starting noise distribution and the target data distribution. Recently Liu et al. (2023b) designed a novel alternative generative model Rectified Flow (RF), which aims to learn straight flow trajectories from noise to data using a sequence of convex optimization problems with close ties to optimal transport. If the trajectory is curved, one must use many Euler discretization steps or novel strategies, such as exponential integrators, to achieve a satisfactory generation quality. In contrast, RF has been shown to theoretically straighten the trajectory through successive rectifications, reducing the number of function evaluations (NFEs) while sampling. It has also been shown empirically that RF may improve the straightness in two rectifications if one can solve the underlying optimization problem within a sufficiently small error. In this paper, we make two key theoretical contributions: 1) we provide the first theoretical analysis of the Wasserstein distance between the sampling distribution of RF and the target distribution. Our error rate is characterized by the number of discretization steps and a new formulation of straightness stronger than that in the original work. 2) In line with the previous empirical findings, we show that, for a rectified flow from a Gaussian to a mixture of two Gaussians, two rectifications are sufficient to achieve a straight flow. Additionally, we also present empirical results on both simulated and real datasets to validate our theoretical findings.

On Differentially Private U Statistics

We consider the problem of privately estimating a parameter $\mathbb{E}[h(X_1,\dots,X_k)]$, where $X_1$, $X_2$, $\dots$, $X_k$ are i.i.d. data from some distribution and $h$ is a permutation-invariant function. Without privacy constraints, standard estimators are U-statistics, which commonly arise in a wide range of problems, including nonparametric signed rank tests, symmetry testing, uniformity testing, and subgraph counts in random networks, and can be shown to be minimum variance unbiased estimators under mild conditions. Despite the recent outpouring of interest in private mean estimation, privatizing U-statistics has received little attention. While existing private mean estimation algorithms can be applied to obtain confidence intervals, we show that they can lead to suboptimal private error, e.g., constant-factor inflation in the leading term, or even $\Theta(1/n)$ rather than $O(1/n^2)$ in degenerate settings. To remedy this, we propose a new thresholding-based approach using \emph{local H\'ajek projections} to reweight different subsets of the data. This leads to nearly optimal private error for non-degenerate U-statistics and a strong indication of near-optimality for degenerate U-statistics.

Transfer Learning for Latent Variable Network Models

We study transfer learning for estimation in latent variable network models. In our setting, the conditional edge probability matrices given the latent variables are represented by $P$ for the source and $Q$ for the target. We wish to estimate $Q$ given two kinds of data: (1) edge data from a subgraph induced by an $o(1)$ fraction of the nodes of $Q$, and (2) edge data from all of $P$. If the source $P$ has no relation to the target $Q$, the estimation error must be $\Omega(1)$. However, we show that if the latent variables are shared, then vanishing error is possible. We give an efficient algorithm that utilizes the ordering of a suitably defined graph distance. Our algorithm achieves $o(1)$ error and does not assume a parametric form on the source or target networks. Next, for the specific case of Stochastic Block Models we prove a minimax lower bound and show that a simple algorithm achieves this rate. Finally, we empirically demonstrate our algorithm's use on real-world and simulated graph transfer problems.

Thresholded Oja does Sparse PCA?

We consider the problem of Sparse Principal Component Analysis (PCA) when the ratio $d/n \rightarrow c > 0$. There has been a lot of work on optimal rates on sparse PCA in the offline setting, where all the data is available for multiple passes. In contrast, when the population eigenvector is $s$-sparse, streaming algorithms that have $O(d)$ storage and $O(nd)$ time complexity either typically require strong initialization conditions or have a suboptimal error. We show that a simple algorithm that thresholds and renormalizes the output of Oja's algorithm (the Oja vector) obtains a near-optimal error rate. This is very surprising because, without thresholding, the Oja vector has a large error. Our analysis centers around bounding the entries of the unnormalized Oja vector, which involves the projection of a product of independent random matrices on a random initial vector. This is nontrivial and novel since previous analyses of Oja's algorithm and matrix products have been done when the trace of the population covariance matrix is bounded while in our setting, this quantity can be as large as $n$.

Keep or toss? A nonparametric score to evaluate solutions for noisy ICA

In this paper, we propose a non-parametric score to evaluate the quality of the solution to an iterative algorithm for Independent Component Analysis (ICA) with arbitrary Gaussian noise. The novelty of this score stems from the fact that it just assumes a finite second moment of the data and uses the characteristic function to evaluate the quality of the estimated mixing matrix without any knowledge of the parameters of the noise distribution. We also provide a new characteristic function-based contrast function for ICA and propose a fixed point iteration to optimize the corresponding objective function. Finally, we propose a theoretical framework to obtain sufficient conditions for the local and global optima of a family of contrast functions for ICA. This framework uses quasi-orthogonalization inherently, and our results extend the classical analysis of cumulant-based objective functions to noisy ICA. We demonstrate the efficacy of our algorithms via experimental results on simulated datasets.

Streaming PCA for Markovian Data

Since its inception in Erikki Oja's seminal paper in 1982, Oja's algorithm has become an established method for streaming principle component analysis (PCA). We study the problem of streaming PCA, where the data-points are sampled from an irreducible, aperiodic, and reversible Markov chain. Our goal is to estimate the top eigenvector of the unknown covariance matrix of the stationary distribution. This setting has implications in situations where data can only be sampled from a Markov Chain Monte Carlo (MCMC) type algorithm, and the goal is to do inference for parameters of the stationary distribution of this chain. Most convergence guarantees for Oja's algorithm in the literature assume that the data-points are sampled IID. For data streams with Markovian dependence, one typically downsamples the data to get a "nearly" independent data stream. In this paper, we obtain the first sharp rate for Oja's algorithm on the entire data, where we remove the logarithmic dependence on $n$ resulting from throwing data away in downsampling strategies.

An Exponentially Increasing Step-size for Parameter Estimation in Statistical Models

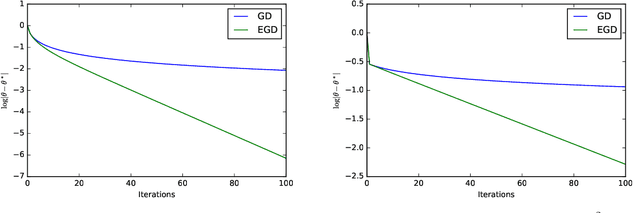
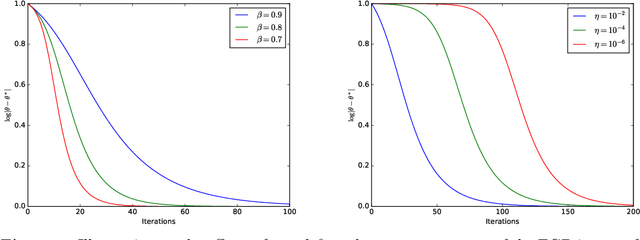
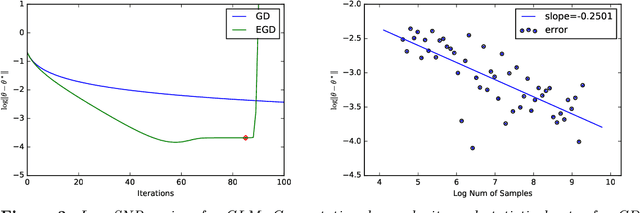
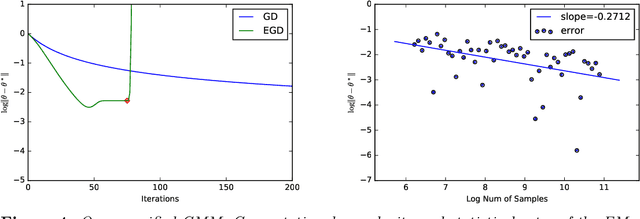
Using gradient descent (GD) with fixed or decaying step-size is standard practice in unconstrained optimization problems. However, when the loss function is only locally convex, such a step-size schedule artificially slows GD down as it cannot explore the flat curvature of the loss function. To overcome that issue, we propose to exponentially increase the step-size of the GD algorithm. Under homogeneous assumptions on the loss function, we demonstrate that the iterates of the proposed \emph{exponential step size gradient descent} (EGD) algorithm converge linearly to the optimal solution. Leveraging that optimization insight, we then consider using the EGD algorithm for solving parameter estimation under non-regular statistical models whose the loss function becomes locally convex when the sample size goes to infinity. We demonstrate that the EGD iterates reach the final statistical radius within the true parameter after a logarithmic number of iterations, which is in stark contrast to a \emph{polynomial} number of iterations of the GD algorithm. Therefore, the total computational complexity of the EGD algorithm is \emph{optimal} and exponentially cheaper than that of the GD for solving parameter estimation in non-regular statistical models. To the best of our knowledge, it resolves a long-standing gap between statistical and algorithmic computational complexities of parameter estimation in non-regular statistical models. Finally, we provide targeted applications of the general theory to several classes of statistical models, including generalized linear models with polynomial link functions and location Gaussian mixture models.

Bootstrapping the error of Oja's Algorithm

We consider the problem of quantifying uncertainty for the estimation error of the leading eigenvector from Oja's algorithm for streaming principal component analysis, where the data are generated IID from some unknown distribution. By combining classical tools from the U-statistics literature with recent results on high-dimensional central limit theorems for quadratic forms of random vectors and concentration of matrix products, we establish a $\chi^2$ approximation result for the $\sin^2$ error between the population eigenvector and the output of Oja's algorithm. Since estimating the covariance matrix associated with the approximating distribution requires knowledge of unknown model parameters, we propose a multiplier bootstrap algorithm that may be updated in an online manner. We establish conditions under which the bootstrap distribution is close to the corresponding sampling distribution with high probability, thereby establishing the bootstrap as a consistent inferential method in an appropriate asymptotic regime.

Higher-Order Correct Multiplier Bootstraps for Count Functionals of Networks

Subgraph counts play a central role in both graph limit theory and network data analysis. In recent years, substantial progress has been made in the area of uncertainty quantification for these functionals; several procedures are now known to be consistent for the problem. In this paper, we propose a new class of multiplier bootstraps for count functionals. We show that a bootstrap procedure with a multiplicative weights exhibits higher-order correctness under appropriate sparsity conditions. Since this bootstrap is computationally expensive, we propose linear and quadratic approximations to the multiplier bootstrap, which correspond to the first and second-order Hayek projections of an approximating U-statistic, respectively. We show that the quadratic bootstrap procedure achieves higher-order correctness under analogous conditions to the multiplicative bootstrap while having much better computational properties. We complement our theoretical results with a simulation study and verify that our procedure offers state-of-the-art performance for several functionals.

On the Theoretical Properties of the Network Jackknife

We study the properties of a leave-node-out jackknife procedure for network data. Under the sparse graphon model, we prove an Efron-Stein-type inequality, showing that the network jackknife leads to conservative estimates of the variance (in expectation) for any network functional that is invariant to node permutation. For a general class of count functionals, we also establish consistency of the network jackknife. We complement our theoretical analysis with a range of simulated and real-data examples and show that the network jackknife offers competitive performance in cases where other resampling methods are known to be valid. In fact, for several network statistics, we see that the jackknife provides more accurate inferences compared to related methods such as subsampling.