Miguel Ángel García-March
Universal representation by Boltzmann machines with Regularised Axons
Oct 22, 2023Abstract:It is widely known that Boltzmann machines are capable of representing arbitrary probability distributions over the values of their visible neurons, given enough hidden ones. However, sampling -- and thus training -- these models can be numerically hard. Recently we proposed a regularisation of the connections of Boltzmann machines, in order to control the energy landscape of the model, paving a way for efficient sampling and training. Here we formally prove that such regularised Boltzmann machines preserve the ability to represent arbitrary distributions. This is in conjunction with controlling the number of energy local minima, thus enabling easy \emph{guided} sampling and training. Furthermore, we explicitly show that regularised Boltzmann machines can store exponentially many arbitrarily correlated visible patterns with perfect retrieval, and we connect them to the Dense Associative Memory networks.
Efficient training of energy-based models via spin-glass control
Oct 03, 2019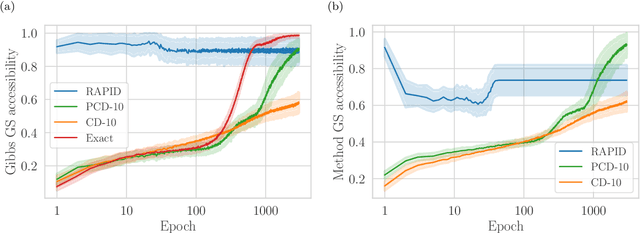
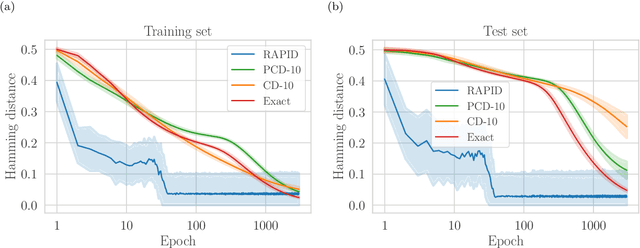
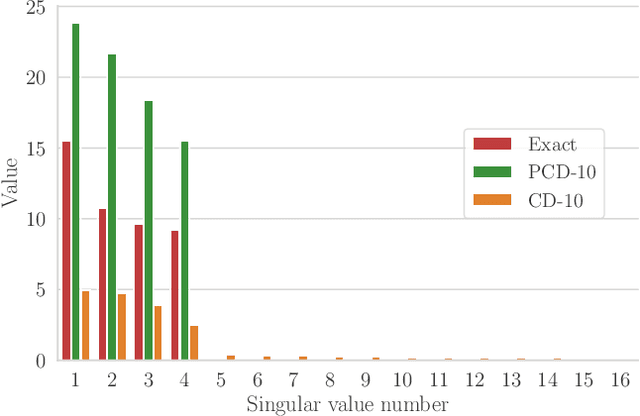
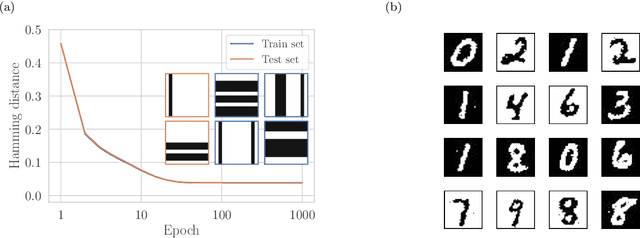
Abstract:We present an efficient method for unsupervised learning using Boltzmann machines. The method is rooted in the control of the spin-glass properties of the Ising model described by the Boltzmann machine's weights. This allows for very easy access to low-energy configurations. We apply RAPID, the combination of Restricting the Axons (RA) of the model and training via Pattern-InDuced correlations (PID), to learn the Bars and Stripes dataset of various sizes and the MNIST dataset. We show how, in these tasks, RAPID quickly outperforms standard techniques for unsupervised learning in generalization ability. Indeed, both the number of epochs needed for effective learning and the computation time per training step are greatly reduced. In its simplest form, PID allows to compute the negative phase of the log-likelihood gradient with no Markov chain Monte Carlo sampling costs at all.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge