Disease control as an optimization problem

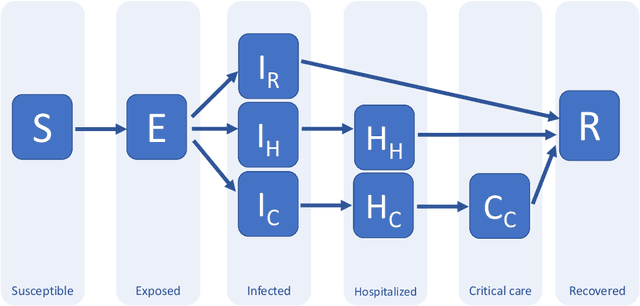
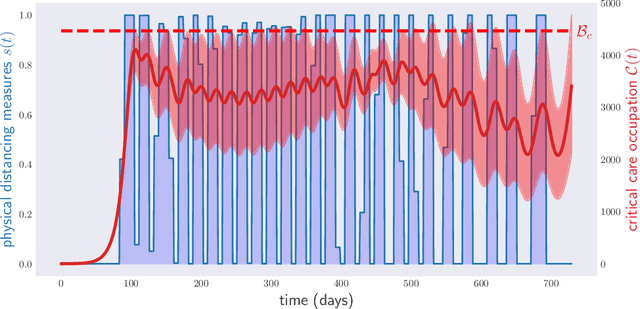
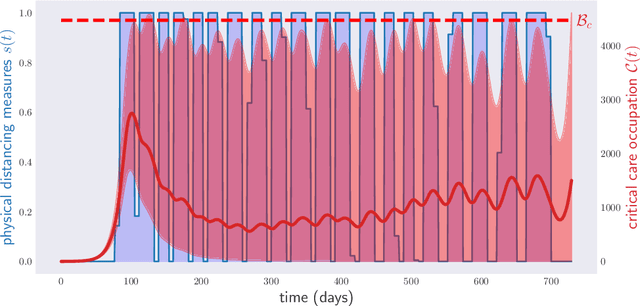
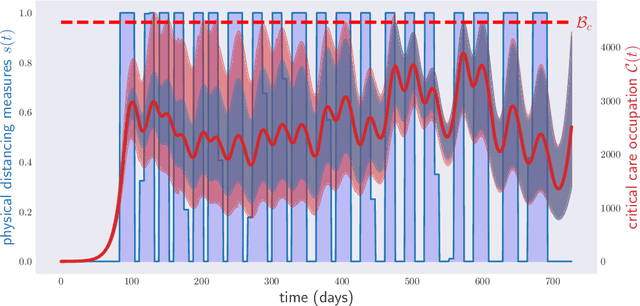
Traditionally, expert epidemiologists devise policies for disease control through a mixture of intuition and brute force. Namely, they use their know-how to narrow down the set of logically conceivable policies to a small family described by a few parameters, following which they conduct a grid search to identify the optimal policy within the set. This scheme is not scalable, in the sense that, when used to optimize over policies which depend on many parameters, it would likely fail to output an optimal disease policy in time for its implementation. In this article, we use techniques from convex optimization theory and machine learning to conduct optimizations over disease policies described by hundreds of parameters. We illustrate our approach by minimizing the total time required to eradicate COVID-19 within the Susceptible-Exposed-Infected-Recovered (SEIR) model proposed by Kissler et al. (March, 2020). We observe that optimal policies are typically very complex, and thus unlikely to be discovered by a human agent.

Quantum Inflation: A General Approach to Quantum Causal Compatibility

Causality is a seminal concept in science: any research discipline, from sociology and medicine to physics and chemistry, aims at understanding the causes that could explain the correlations observed among some measured variables. While several methods exist to characterize classical causal models, no general construction is known for the quantum case. In this work we present quantum inflation, a systematic technique to falsify if a given quantum causal model is compatible with some observed correlations. We demonstrate the power of the technique by reproducing known results and solving open problems for some paradigmatic examples of causal networks. Our results may find an application in many fields: from the characterization of correlations in quantum networks to the study of quantum effects in thermodynamic and biological processes.

The inflation technique solves completely the classical inference problem

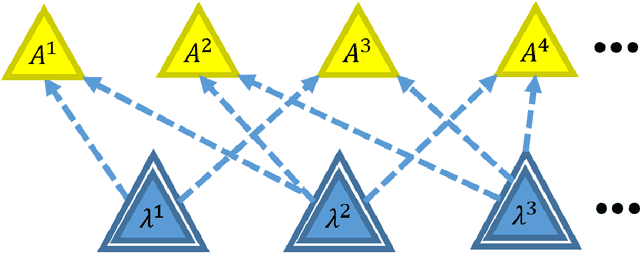
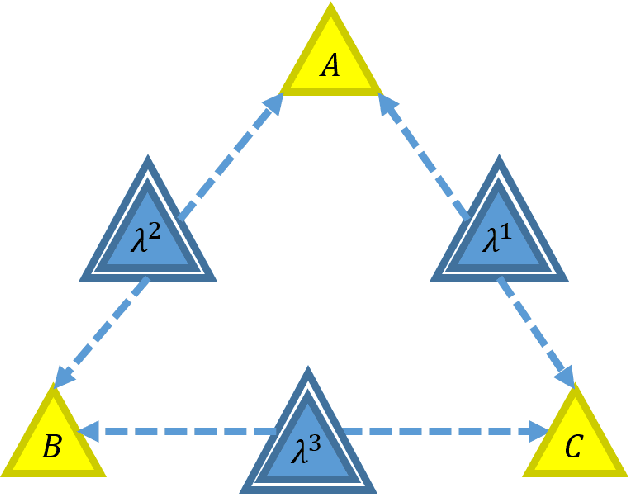
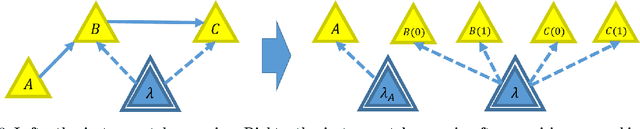
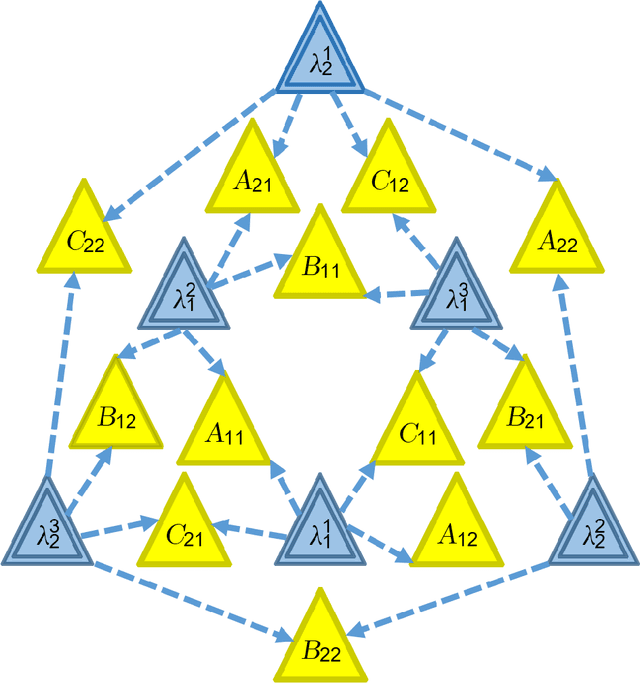
The causal inference problem consists in determining whether a probability distribution over a set of observed variables is compatible with a given causal structure. In [arXiv:1609.00672], one of us introduced a hierarchy of necessary linear programming constraints which all the observed distributions compatible with the considered causal structure must satisfy. In this work, we prove that the inflation hierarchy is complete, i.e., any distribution of the observed variables which does not admit a realization within the considered causal structure will fail one of the inflation tests. More quantitatively, we show that any distribution of measurable events satisfying the $n^{th}$ inflation test is $O\left(\frac{1}{\sqrt{n}}\right)$-close in Euclidean norm to a distribution realizable within the given causal structure. In addition, we show that the corresponding $n^{th}$-order relaxation of the dual problem consisting in maximizing a $k^{th}$ degree polynomial on the observed variables is $O\left(\frac{k^2}{n}\right)$-close to the optimal solution.