Neural simulation-based inference of the Higgs trilinear self-coupling via off-shell Higgs production

One of the forthcoming major challenges in particle physics is the experimental determination of the Higgs trilinear self-coupling. While efforts have largely focused on on-shell double- and single-Higgs production in proton-proton collisions, off-shell Higgs production has also been proposed as a valuable complementary probe. In this article, we design a hybrid neural simulation-based inference (NSBI) approach to construct a likelihood of the Higgs signal incorporating modifications from the Standard Model effective field theory (SMEFT), relevant background processes, and quantum interference effects. It leverages the training efficiency of matrix-element-enhanced techniques, which are vital for robust SMEFT applications, while also incorporating the practical advantages of classification-based methods for effective background estimates. We demonstrate that our NSBI approach achieves sensitivity close to the theoretical optimum and provide expected constraints for the high-luminosity upgrade of the Large Hadron Collider. While we primarily concentrate on the Higgs trilinear self-coupling, we also consider constraints on other SMEFT operators that affect off-shell Higgs production.

Learning Broken Symmetries with Approximate Invariance

Recognizing symmetries in data allows for significant boosts in neural network training, which is especially important where training data are limited. In many cases, however, the exact underlying symmetry is present only in an idealized dataset, and is broken in actual data, due to asymmetries in the detector, or varying response resolution as a function of particle momentum. Standard approaches, such as data augmentation or equivariant networks fail to represent the nature of the full, broken symmetry, effectively overconstraining the response of the neural network. We propose a learning model which balances the generality and asymptotic performance of unconstrained networks with the rapid learning of constrained networks. This is achieved through a dual-subnet structure, where one network is constrained by the symmetry and the other is not, along with a learned symmetry factor. In a simplified toy example that demonstrates violation of Lorentz invariance, our model learns as rapidly as symmetry-constrained networks but escapes its performance limitations.

FAIR Universe HiggsML Uncertainty Challenge Competition

The FAIR Universe -- HiggsML Uncertainty Challenge focuses on measuring the physics properties of elementary particles with imperfect simulators due to differences in modelling systematic errors. Additionally, the challenge is leveraging a large-compute-scale AI platform for sharing datasets, training models, and hosting machine learning competitions. Our challenge brings together the physics and machine learning communities to advance our understanding and methodologies in handling systematic (epistemic) uncertainties within AI techniques.

Full Event Particle-Level Unfolding with Variable-Length Latent Variational Diffusion

The measurements performed by particle physics experiments must account for the imperfect response of the detectors used to observe the interactions. One approach, unfolding, statistically adjusts the experimental data for detector effects. Recently, generative machine learning models have shown promise for performing unbinned unfolding in a high number of dimensions. However, all current generative approaches are limited to unfolding a fixed set of observables, making them unable to perform full-event unfolding in the variable dimensional environment of collider data. A novel modification to the variational latent diffusion model (VLD) approach to generative unfolding is presented, which allows for unfolding of high- and variable-dimensional feature spaces. The performance of this method is evaluated in the context of semi-leptonic top quark pair production at the Large Hadron Collider.

Generalizing to new calorimeter geometries with Geometry-Aware Autoregressive Models (GAAMs) for fast calorimeter simulation

Generation of simulated detector response to collision products is crucial to data analysis in particle physics, but computationally very expensive. One subdetector, the calorimeter, dominates the computational time due to the high granularity of its cells and complexity of the interaction. Generative models can provide more rapid sample production, but currently require significant effort to optimize performance for specific detector geometries, often requiring many networks to describe the varying cell sizes and arrangements, which do not generalize to other geometries. We develop a {\it geometry-aware} autoregressive model, which learns how the calorimeter response varies with geometry, and is capable of generating simulated responses to unseen geometries without additional training. The geometry-aware model outperforms a baseline, unaware model by 50\% in metrics such as the Wasserstein distance between generated and true distributions of key quantities which summarize the simulated response. A single geometry-aware model could replace the hundreds of generative models currently designed for calorimeter simulation by physicists analyzing data collected at the Large Hadron Collider. For the study of future detectors, such a foundational model will be a crucial tool, dramatically reducing the large upfront investment usually needed to develop generative calorimeter models.

End-To-End Latent Variational Diffusion Models for Inverse Problems in High Energy Physics

High-energy collisions at the Large Hadron Collider (LHC) provide valuable insights into open questions in particle physics. However, detector effects must be corrected before measurements can be compared to certain theoretical predictions or measurements from other detectors. Methods to solve this \textit{inverse problem} of mapping detector observations to theoretical quantities of the underlying collision are essential parts of many physics analyses at the LHC. We investigate and compare various generative deep learning methods to approximate this inverse mapping. We introduce a novel unified architecture, termed latent variation diffusion models, which combines the latent learning of cutting-edge generative art approaches with an end-to-end variational framework. We demonstrate the effectiveness of this approach for reconstructing global distributions of theoretical kinematic quantities, as well as for ensuring the adherence of the learned posterior distributions to known physics constraints. Our unified approach achieves a distribution-free distance to the truth of over 20 times less than non-latent state-of-the-art baseline and 3 times less than traditional latent diffusion models.

Geometry-aware Autoregressive Models for Calorimeter Shower Simulations

Calorimeter shower simulations are often the bottleneck in simulation time for particle physics detectors. A lot of effort is currently spent on optimizing generative architectures for specific detector geometries, which generalize poorly. We develop a geometry-aware autoregressive model on a range of calorimeter geometries such that the model learns to adapt its energy deposition depending on the size and position of the cells. This is a key proof-of-concept step towards building a model that can generalize to new unseen calorimeter geometries with little to no additional training. Such a model can replace the hundreds of generative models used for calorimeter simulation in a Large Hadron Collider experiment. For the study of future detectors, such a model will dramatically reduce the large upfront investment usually needed to generate simulations.

Interpretable Uncertainty Quantification in AI for HEP

Estimating uncertainty is at the core of performing scientific measurements in HEP: a measurement is not useful without an estimate of its uncertainty. The goal of uncertainty quantification (UQ) is inextricably linked to the question, "how do we physically and statistically interpret these uncertainties?" The answer to this question depends not only on the computational task we aim to undertake, but also on the methods we use for that task. For artificial intelligence (AI) applications in HEP, there are several areas where interpretable methods for UQ are essential, including inference, simulation, and control/decision-making. There exist some methods for each of these areas, but they have not yet been demonstrated to be as trustworthy as more traditional approaches currently employed in physics (e.g., non-AI frequentist and Bayesian methods). Shedding light on the questions above requires additional understanding of the interplay of AI systems and uncertainty quantification. We briefly discuss the existing methods in each area and relate them to tasks across HEP. We then discuss recommendations for avenues to pursue to develop the necessary techniques for reliable widespread usage of AI with UQ over the next decade.

A Cautionary Tale of Decorrelating Theory Uncertainties

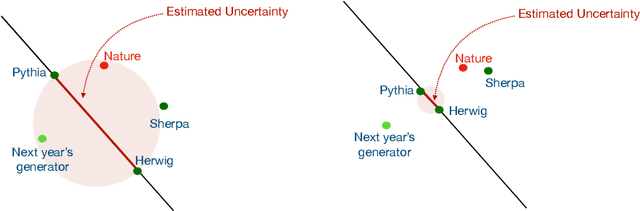
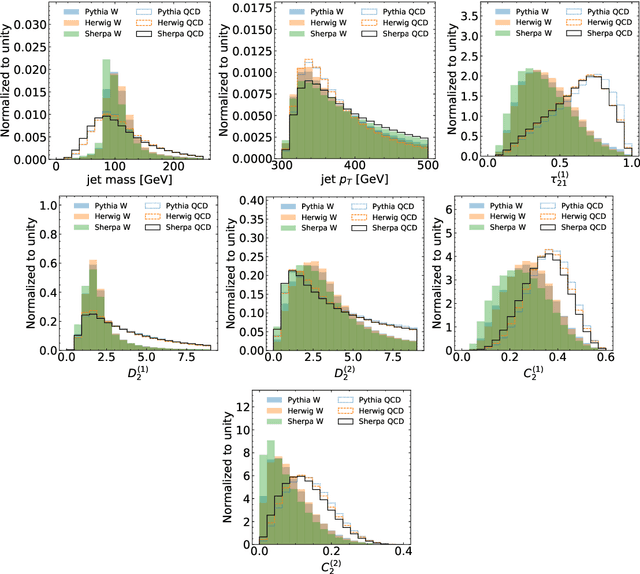
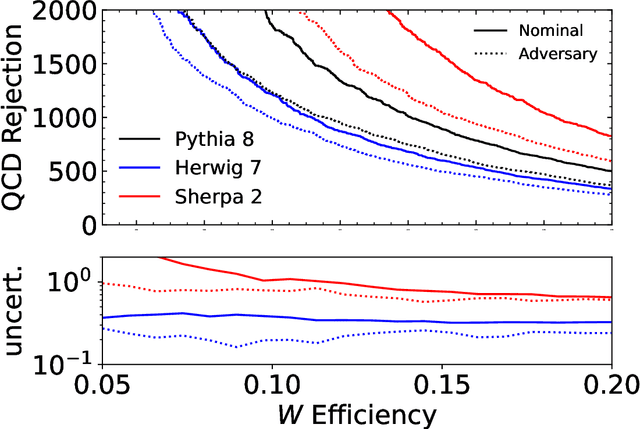
A variety of techniques have been proposed to train machine learning classifiers that are independent of a given feature. While this can be an essential technique for enabling background estimation, it may also be useful for reducing uncertainties. We carefully examine theory uncertainties, which typically do not have a statistical origin. We will provide explicit examples of two-point (fragmentation modeling) and continuous (higher-order corrections) uncertainties where decorrelating significantly reduces the apparent uncertainty while the actual uncertainty is much larger. These results suggest that caution should be taken when using decorrelation for these types of uncertainties as long as we do not have a complete decomposition into statistically meaningful components.