On the benefits of maximum likelihood estimation for Regression and Forecasting

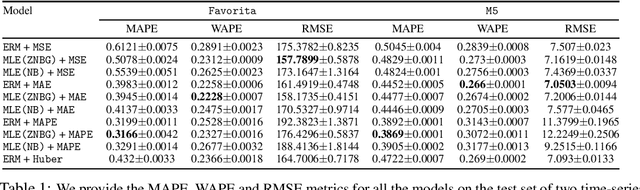
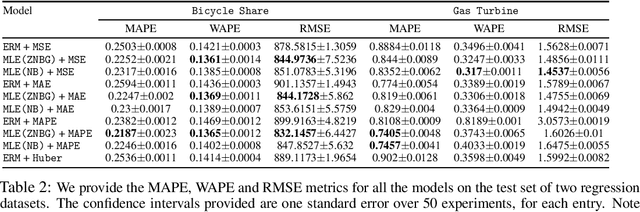
We advocate for a practical Maximum Likelihood Estimation (MLE) approach for regression and forecasting, as an alternative to the typical approach of Empirical Risk Minimization (ERM) for a specific target metric. This approach is better suited to capture inductive biases such as prior domain knowledge in datasets, and can output post-hoc estimators at inference time that can optimize different types of target metrics. We present theoretical results to demonstrate that our approach is always competitive with any estimator for the target metric under some general conditions, and in many practical settings (such as Poisson Regression) can actually be much superior to ERM. We demonstrate empirically that our method instantiated with a well-designed general purpose mixture likelihood family can obtain superior performance over ERM for a variety of tasks across time-series forecasting and regression datasets with different data distributions.

Hierarchically Regularized Deep Forecasting

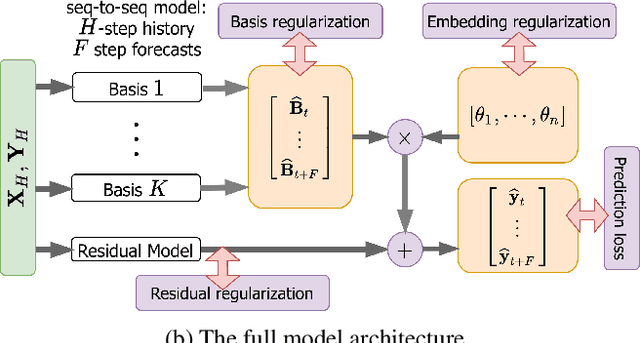
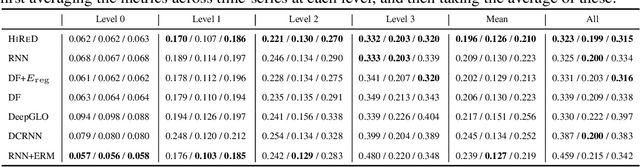
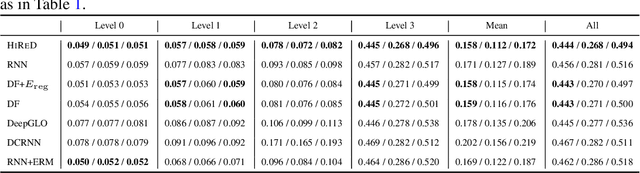
Hierarchical forecasting is a key problem in many practical multivariate forecasting applications - the goal is to simultaneously predict a large number of correlated time series that are arranged in a pre-specified aggregation hierarchy. The challenge is to exploit the hierarchical correlations to simultaneously obtain good prediction accuracy for time series at different levels of the hierarchy. In this paper, we propose a new approach for hierarchical forecasting based on decomposing the time series along a global set of basis time series and modeling hierarchical constraints using the coefficients of the basis decomposition for each time series. Unlike past methods, our approach is scalable at inference-time (forecasting for a specific time series only needs access to its own data) while (approximately) preserving coherence among the time series forecasts. We experiment on several publicly available datasets and demonstrate significantly improved overall performance on forecasts at different levels of the hierarchy, compared to existing state-of-the-art hierarchical reconciliation methods.

One Network Fits All? Modular versus Monolithic Task Formulations in Neural Networks

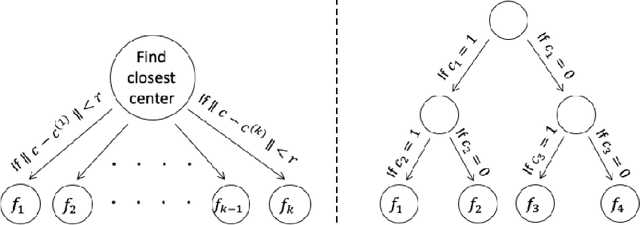
Can deep learning solve multiple tasks simultaneously, even when they are unrelated and very different? We investigate how the representations of the underlying tasks affect the ability of a single neural network to learn them jointly. We present theoretical and empirical findings that a single neural network is capable of simultaneously learning multiple tasks from a combined data set, for a variety of methods for representing tasks -- for example, when the distinct tasks are encoded by well-separated clusters or decision trees over certain task-code attributes. More concretely, we present a novel analysis that shows that families of simple programming-like constructs for the codes encoding the tasks are learnable by two-layer neural networks with standard training. We study more generally how the complexity of learning such combined tasks grows with the complexity of the task codes; we find that combining many tasks may incur a sample complexity penalty, even though the individual tasks are easy to learn. We provide empirical support for the usefulness of the learning bounds by training networks on clusters, decision trees, and SQL-style aggregation.

Upper Confidence Bounds for Combining Stochastic Bandits

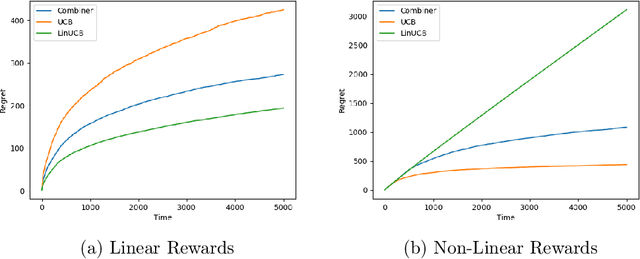
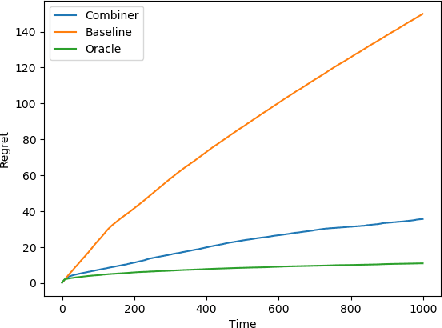
We provide a simple method to combine stochastic bandit algorithms. Our approach is based on a "meta-UCB" procedure that treats each of $N$ individual bandit algorithms as arms in a higher-level $N$-armed bandit problem that we solve with a variant of the classic UCB algorithm. Our final regret depends only on the regret of the base algorithm with the best regret in hindsight. This approach provides an easy and intuitive alternative strategy to the CORRAL algorithm for adversarial bandits, without requiring the stability conditions imposed by CORRAL on the base algorithms. Our results match lower bounds in several settings, and we provide empirical validation of our algorithm on misspecified linear bandit and model selection problems.

Learning the gravitational force law and other analytic functions

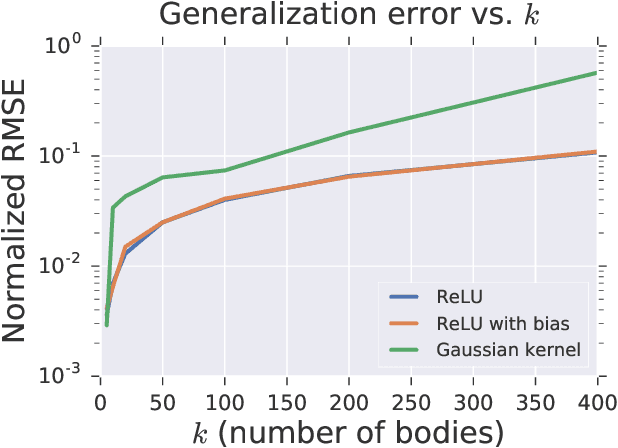
Large neural network models have been successful in learning functions of importance in many branches of science, including physics, chemistry and biology. Recent theoretical work has shown explicit learning bounds for wide networks and kernel methods on some simple classes of functions, but not on more complex functions which arise in practice. We extend these techniques to provide learning bounds for analytic functions on the sphere for any kernel method or equivalent infinitely-wide network with the corresponding activation function trained with SGD. We show that a wide, one-hidden layer ReLU network can learn analytic functions with a number of samples proportional to the derivative of a related function. Many functions important in the sciences are therefore efficiently learnable. As an example, we prove explicit bounds on learning the many-body gravitational force function given by Newton's law of gravitation. Our theoretical bounds suggest that very wide ReLU networks (and the corresponding NTK kernel) are better at learning analytic functions as compared to kernel learning with Gaussian kernels. We present experimental evidence that the many-body gravitational force function is easier to learn with ReLU networks as compared to networks with exponential activations.

On the Learnability of Deep Random Networks

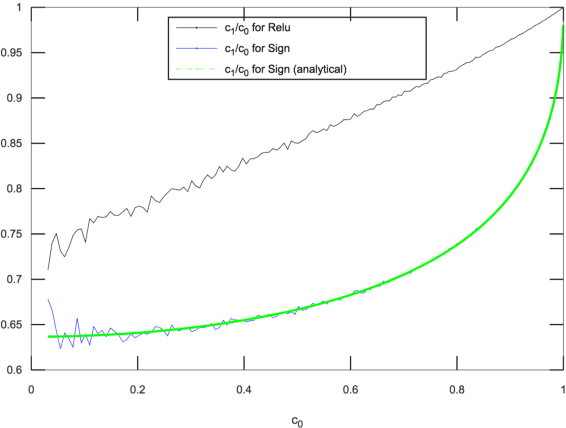
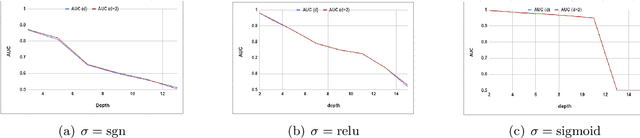
In this paper we study the learnability of deep random networks from both theoretical and practical points of view. On the theoretical front, we show that the learnability of random deep networks with sign activation drops exponentially with its depth. On the practical front, we find that the learnability drops sharply with depth even with the state-of-the-art training methods, suggesting that our stylized theoretical results are closer to reality.

Submodular meets Spectral: Greedy Algorithms for Subset Selection, Sparse Approximation and Dictionary Selection

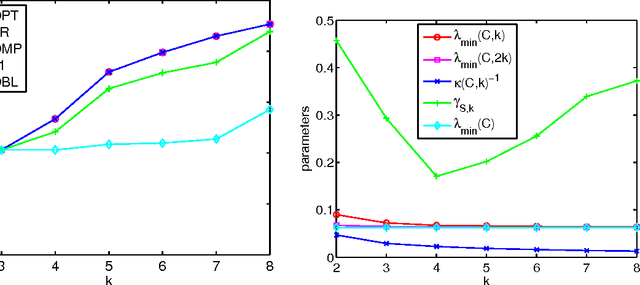
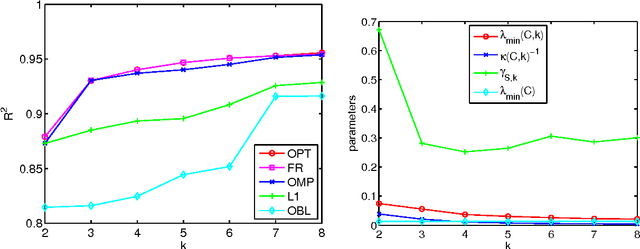
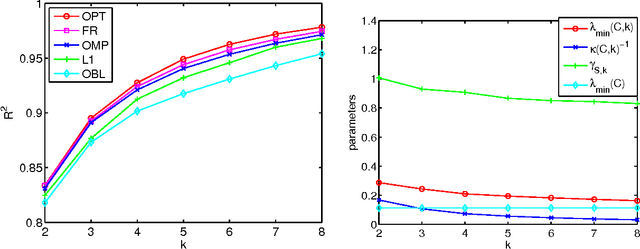
We study the problem of selecting a subset of k random variables from a large set, in order to obtain the best linear prediction of another variable of interest. This problem can be viewed in the context of both feature selection and sparse approximation. We analyze the performance of widely used greedy heuristics, using insights from the maximization of submodular functions and spectral analysis. We introduce the submodularity ratio as a key quantity to help understand why greedy algorithms perform well even when the variables are highly correlated. Using our techniques, we obtain the strongest known approximation guarantees for this problem, both in terms of the submodularity ratio and the smallest k-sparse eigenvalue of the covariance matrix. We further demonstrate the wide applicability of our techniques by analyzing greedy algorithms for the dictionary selection problem, and significantly improve the previously known guarantees. Our theoretical analysis is complemented by experiments on real-world and synthetic data sets; the experiments show that the submodularity ratio is a stronger predictor of the performance of greedy algorithms than other spectral parameters.