Continuous and Discrete LTI Systems

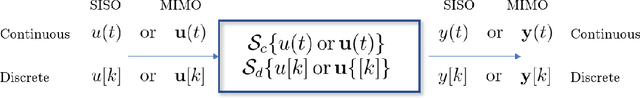
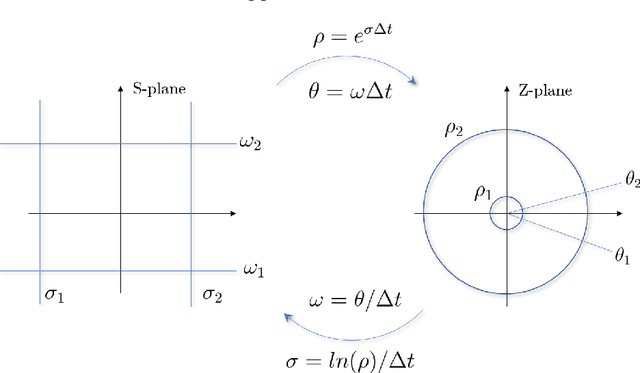
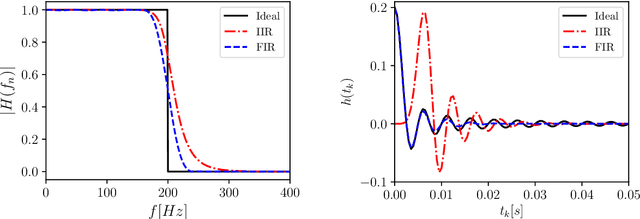
This chapter reviews the fundamentals of continuous and discrete Linear Time-Invariant (LTI) systems with Single Input-Single Output (SISO). We start from the general notions of signals and systems, the signal representation problem and the related orthogonal bases in discrete and continuous forms. We then move to the key properties of LTI systems and discuss their eigenfunctions, the input-output relations in the time and frequency domains, the conformal mapping linking the continuous and the discrete formulations, and the modeling via differential and difference equations. Finally, we close with two important applications: (linear) models for time series analysis and forecasting and (linear) digital filters for multi-resolution analysis. This chapter contains seven exercises, the solution of which is provided in the book's webpage.

Transfer Learning for Clinical Time Series Analysis using Deep Neural Networks

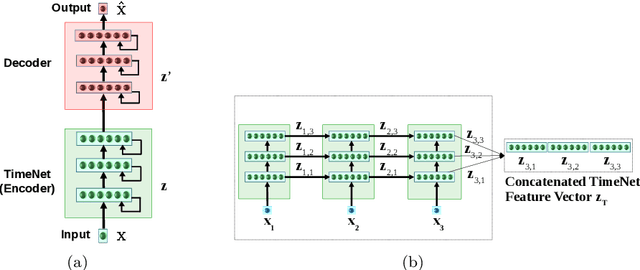
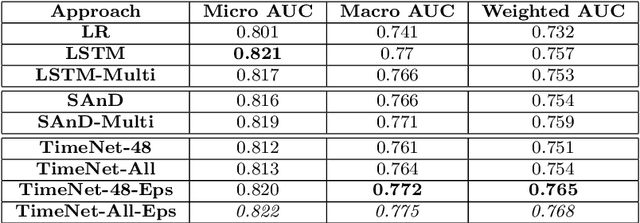
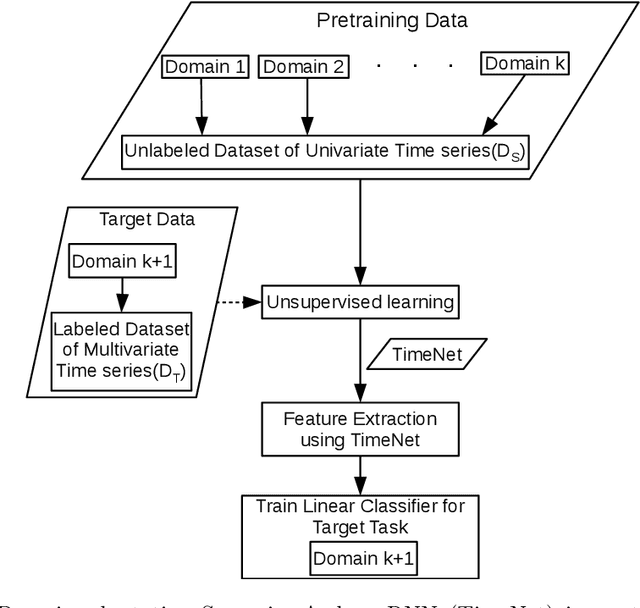
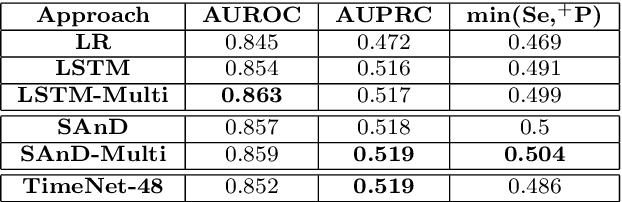
Deep neural networks have shown promising results for various clinical prediction tasks. However, training deep networks such as those based on Recurrent Neural Networks (RNNs) requires large labeled data, significant hyper-parameter tuning effort and expertise, and high computational resources. In this work, we investigate as to what extent can transfer learning address these issues when using deep RNNs to model multivariate clinical time series. We consider two scenarios for transfer learning using RNNs: i) domain-adaptation, i.e., leveraging a deep RNN - namely, TimeNet - pre-trained for feature extraction on time series from diverse domains, and adapting it for feature extraction and subsequent target tasks in healthcare domain, ii) task-adaptation, i.e., pre-training a deep RNN - namely, HealthNet - on diverse tasks in healthcare domain, and adapting it to new target tasks in the same domain. We evaluate the above approaches on publicly available MIMIC-III benchmark dataset, and demonstrate that (a) computationally-efficient linear models trained using features extracted via pre-trained RNNs outperform or, in the worst case, perform as well as deep RNNs and statistical hand-crafted features based models trained specifically for target task; (b) models obtained by adapting pre-trained models for target tasks are significantly more robust to the size of labeled data compared to task-specific RNNs, while also being computationally efficient. We, therefore, conclude that pre-trained deep models like TimeNet and HealthNet allow leveraging the advantages of deep learning for clinical time series analysis tasks, while also minimize dependence on hand-crafted features, deal robustly with scarce labeled training data scenarios without overfitting, as well as reduce dependence on expertise and resources required to train deep networks from scratch.

Time series analysis with dynamic law exploration

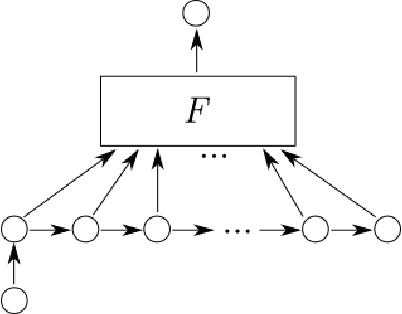
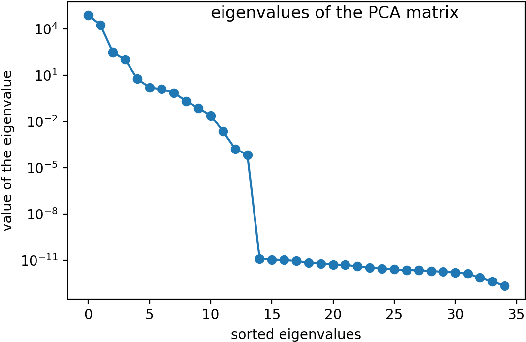
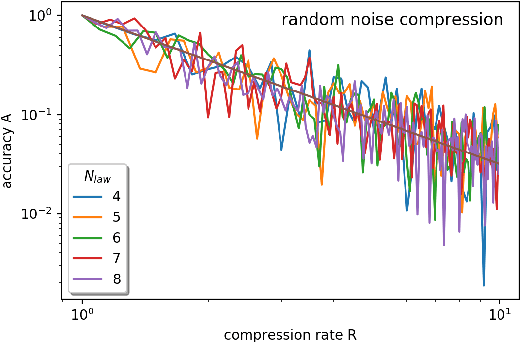
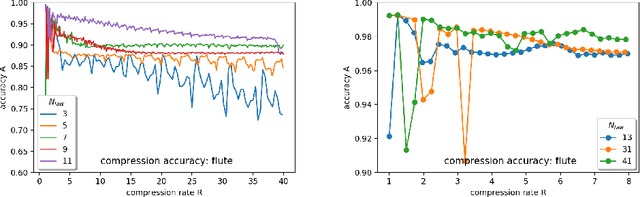
In this paper we examine, how the dynamic laws governing the time evolution of a time series can be identified. We give a finite difference equation as well as a differential equation representation for that. We also study, how the required symmetries, like time reversal can be imposed on the laws. We study the compression performance of linear laws on sound data.

Hyper Attention Recurrent Neural Network: Tackling Temporal Covariate Shift in Time Series Analysis

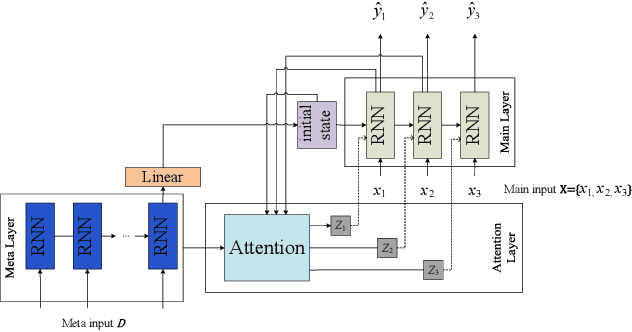
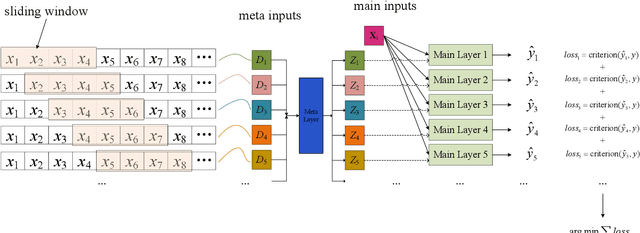
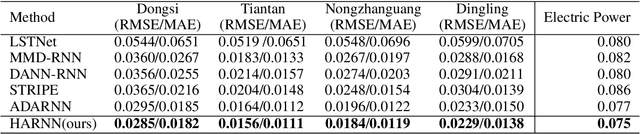
Analyzing long time series with RNNs often suffers from infeasible training. Segmentation is therefore commonly used in data pre-processing. However, in non-stationary time series, there exists often distribution shift among different segments. RNN is easily swamped in the dilemma of fitting bias in these segments due to the lack of global information, leading to poor generalization, known as Temporal Covariate Shift (TCS) problem, which is only addressed by a recently proposed RNN-based model. One of the assumptions in TCS is that the distribution of all divided intervals under the same segment are identical. This assumption, however, may not be true on high-frequency time series, such as traffic flow, that also have large stochasticity. Besides, macro information across long periods isn't adequately considered in the latest RNN-based methods. To address the above issues, we propose Hyper Attention Recurrent Neural Network (HARNN) for the modeling of temporal patterns containing both micro and macro information. An HARNN consists of a meta layer for parameter generation and an attention-enabled main layer for inference. High-frequency segments are transformed into low-frequency segments and fed into the meta layers, while the first main layer consumes the same high-frequency segments as conventional methods. In this way, each low-frequency segment in the meta inputs generates a unique main layer, enabling the integration of both macro information and micro information for inference. This forces all main layers to predict the same target which fully harnesses the common knowledge in varied distributions when capturing temporal patterns. Evaluations on multiple benchmarks demonstrated that our model outperforms a couple of RNN-based methods on a federation of key metrics.

TSViz: Demystification of Deep Learning Models for Time-Series Analysis

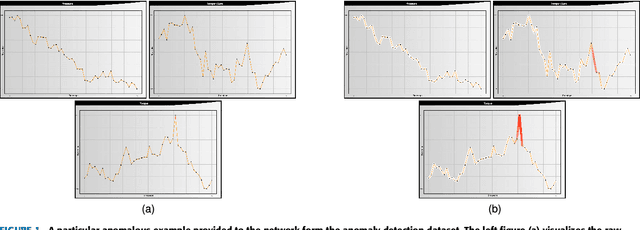
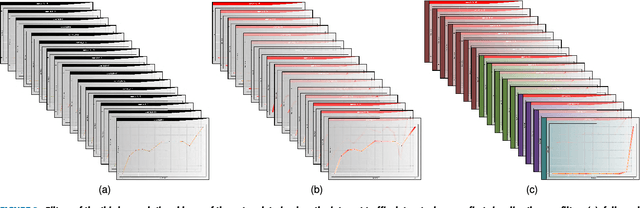
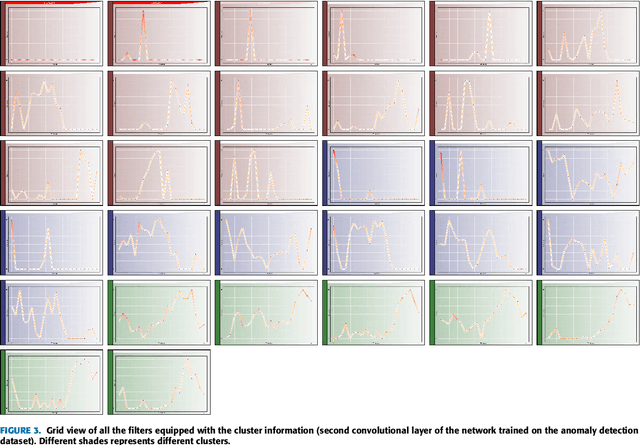
This paper presents a novel framework for demystification of convolutional deep learning models for time series analysis. This is a step towards making informed/explainable decisions in the domain of time series, powered by deep learning. There have been numerous efforts to increase the interpretability of image-centric deep neural network models, where the learned features are more intuitive to visualize. Visualization in time-series is much more complicated as there is no direct interpretation of the filters and inputs as compared to image modality. In addition, little or no concentration has been devoted for the development of such tools in the domain of time-series in the past. The visualization engine of the presented framework provides possibilities to explore and analyze a network from different dimensions at four different levels of abstraction. This enables the user to uncover different aspects of the model which includes important filters, filter clusters, and input saliency maps. These representations allow to understand the network features so that the acceptability of deep networks for time-series data can be enhanced. This is extremely important in domains like finance, industry 4.0, self-driving cars, health-care, counter-terrorism etc., where reasons for reaching a particular prediction are equally important as the prediction itself. The framework \footnote{Framework download link: https://hidden.for.blind.review} can also aid in discovery of the filters which are contributing nothing to the final prediction, hence, can be pruned without any significant loss in performance.

Discovering Predictable Latent Factors for Time Series Forecasting

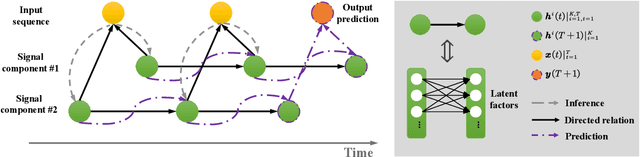
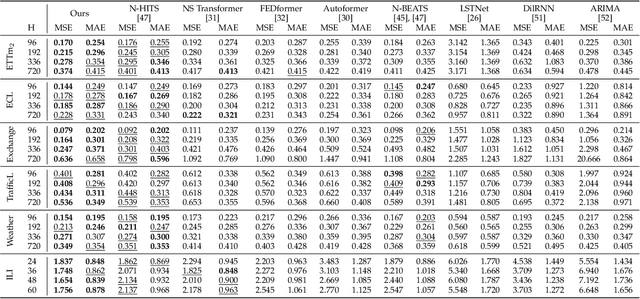
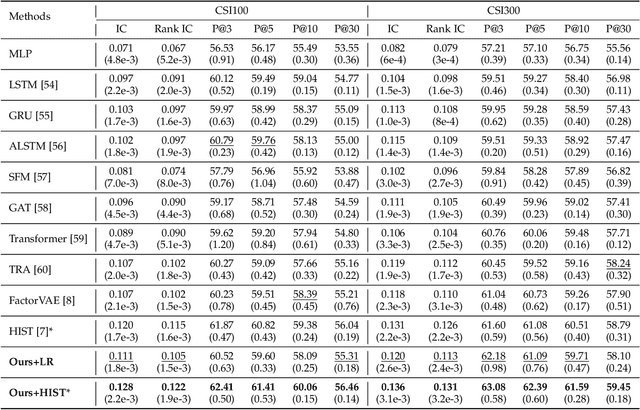
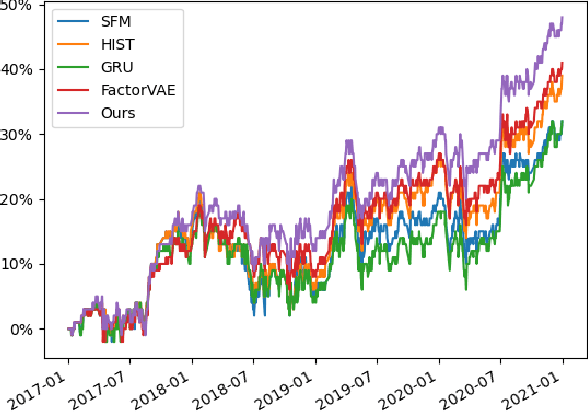
Modern time series forecasting methods, such as Transformer and its variants, have shown strong ability in sequential data modeling. To achieve high performance, they usually rely on redundant or unexplainable structures to model complex relations between variables and tune the parameters with large-scale data. Many real-world data mining tasks, however, lack sufficient variables for relation reasoning, and therefore these methods may not properly handle such forecasting problems. With insufficient data, time series appear to be affected by many exogenous variables, and thus, the modeling becomes unstable and unpredictable. To tackle this critical issue, in this paper, we develop a novel algorithmic framework for inferring the intrinsic latent factors implied by the observable time series. The inferred factors are used to form multiple independent and predictable signal components that enable not only sparse relation reasoning for long-term efficiency but also reconstructing the future temporal data for accurate prediction. To achieve this, we introduce three characteristics, i.e., predictability, sufficiency, and identifiability, and model these characteristics via the powerful deep latent dynamics models to infer the predictable signal components. Empirical results on multiple real datasets show the efficiency of our method for different kinds of time series forecasting. The statistical analysis validates the predictability of the learned latent factors.

Brazilian tailing dam collapse, retrospective precursory monitoring of InSAR data using spectral analysis of time series

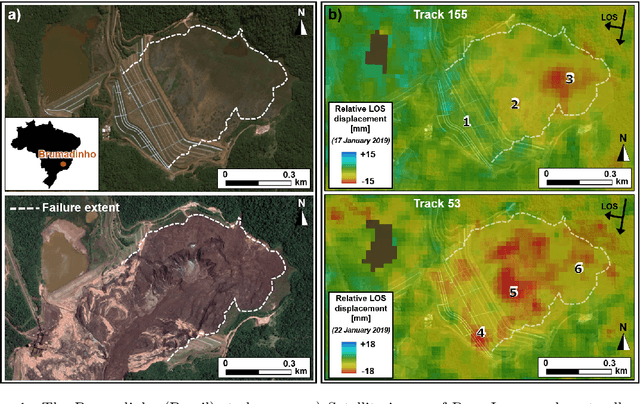
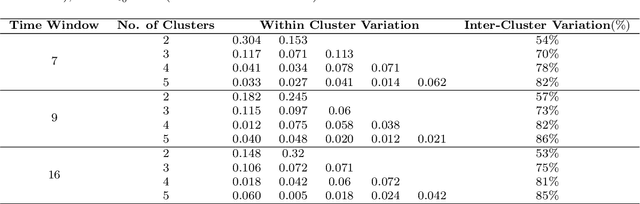
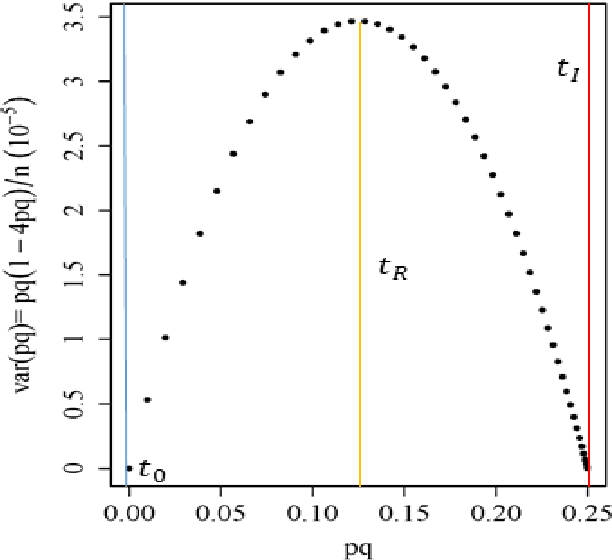
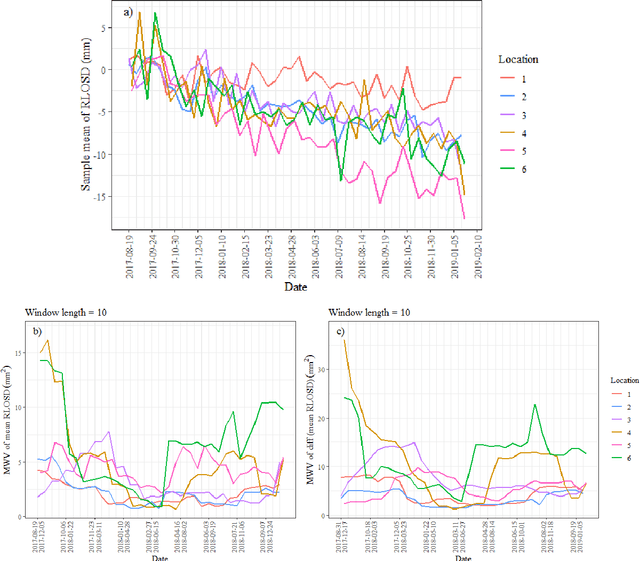
Slope failures possess destructive power that can cause significant damage to both life and infrastructure. Monitoring slopes prone to instabilities is therefore critical in mitigating the risk posed by their failure. The purpose of slope monitoring is to detect precursory signs of stability issues, such as changes in the rate of displacement with which a slope is deforming. This information can then be used to predict the timing or probability of an imminent failure in order to provide an early warning. In this study, a more objective, statistical-learning algorithm is proposed to detect and characterise the risk of a slope failure, based on spectral analysis of serially correlated displacement time series data. The algorithm is applied to satellite-based interferometric synthetic radar (InSAR) displacement time series data to retrospectively analyse the risk of the 2019 Brumadinho tailings dam collapse in Brazil. Two potential risk milestones are identified and signs of a definitive but emergent risk (27 February 2018 to 26 August 2018) and imminent risk of collapse of the tailings dam (27 June 2018 to 24 December 2018) are detected by the algorithm. Importantly, this precursory indication of risk of failure is detected as early as at least five months prior to the dam collapse on 25 January 2019. The results of this study demonstrate that the combination of spectral methods and second order statistical properties of InSAR displacement time series data can reveal signs of a transition into an unstable deformation regime, and that this algorithm can provide sufficient early warning that could help mitigate catastrophic slope failures.

Neural ODEs as Feedback Policies for Nonlinear Optimal Control

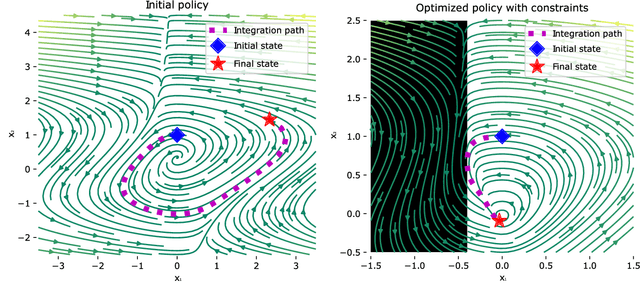
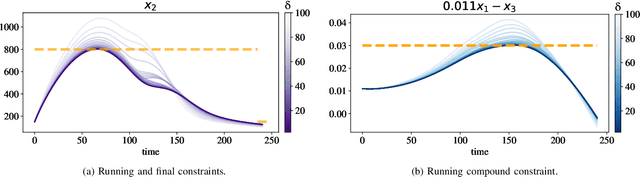
Neural ordinary differential equations (Neural ODEs) model continuous time dynamics as differential equations parametrized with neural networks. Thanks to their modeling flexibility, they have been adopted for multiple tasks where the continuous time nature of the process is specially relevant, as in system identification and time series analysis. When applied in a control setting, it is possible to adapt their use to approximate optimal nonlinear feedback policies. This formulation follows the same approach as policy gradients in reinforcement learning, covering the case where the environment consists of known deterministic dynamics given by a system of differential equations. The white box nature of the model specification allows the direct calculation of policy gradients through sensitivity analysis, avoiding the inexact and inefficient gradient estimation through sampling. In this work we propose the use of a neural control policy posed as a Neural ODE to solve general nonlinear optimal control problems while satisfying both state and control constraints, which are crucial for real world scenarios. Since the state feedback policy partially modifies the model dynamics, the whole space phase of the system is reshaped upon the optimization. This approach is a sensible approximation to the historically intractable closed loop solution of nonlinear control problems that efficiently exploits the availability of a dynamical system model.

Interpretable Transformer for Water Level Forecasting

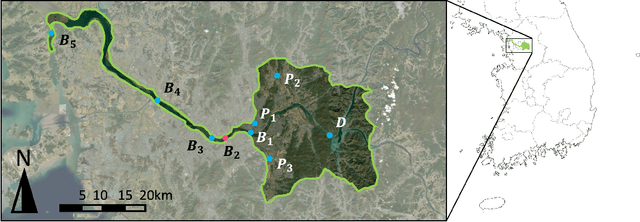
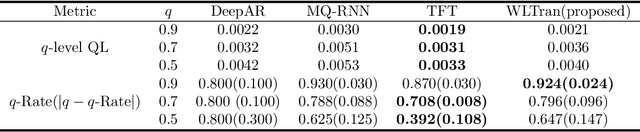
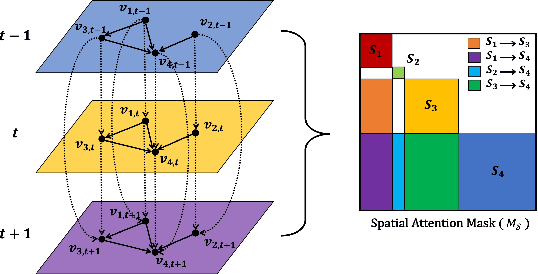
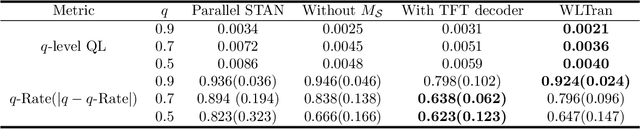
Forecasting the water level of the Han river is important to control the traffic and avoid natural disasters. There are many variables related to the Han river and they are intricately connected. In this work, we propose a novel transformer that exploits the causal relationship based on the prior knowledge among the variables and forecasts the four bridges of the Han river: Cheongdam, Jamsu, Hangang, and Haengju. Our proposed model considers both spatial and temporal causation by formalizing the causal structure as a multilayer network and using masking methods. Due to this approach, we can have the interpretability that consistent with prior knowledge. Additionally, we propose a novel recalibration method and loss function for high accuracy of extreme risk in time series. In real data analysis, we use the Han river dataset from 2016 to 2021, and compare the proposed model with deep learning models.

Novel Features for Time Series Analysis: A Complex Networks Approach

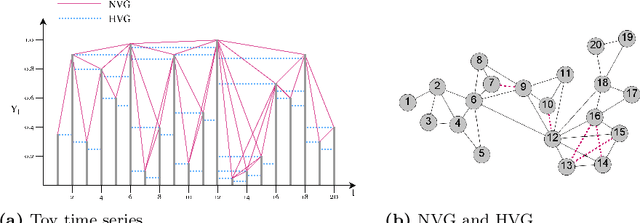
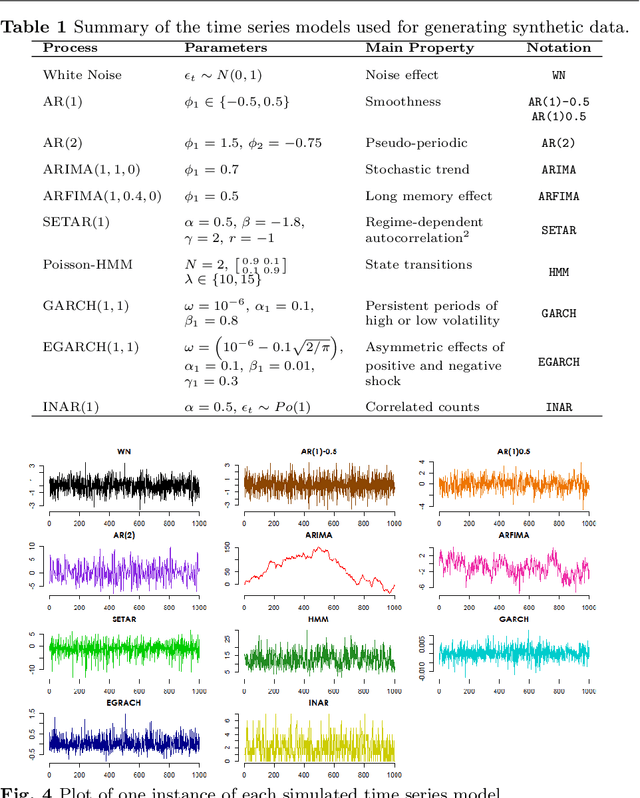
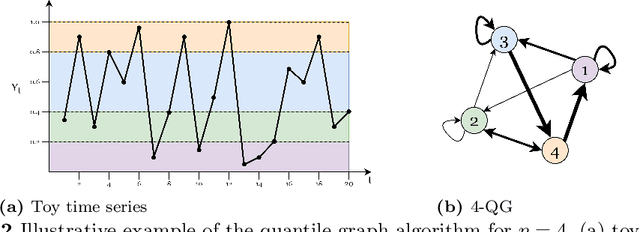
Time series data are ubiquitous in several domains as climate, economics and health care. Mining features from these time series is a crucial task with a multidisciplinary impact. Usually, these features are obtained from structural characteristics of time series, such as trend, seasonality and autocorrelation, sometimes requiring data transformations and parametric models. A recent conceptual approach relies on time series mapping to complex networks, where the network science methodologies can help characterize time series. In this paper, we consider two mapping concepts, visibility and transition probability and propose network topological measures as a new set of time series features. To evaluate the usefulness of the proposed features, we address the problem of time series clustering. More specifically, we propose a clustering method that consists in mapping the time series into visibility graphs and quantile graphs, calculating global topological metrics of the resulting networks, and using data mining techniques to form clusters. We apply this method to a data sets of synthetic and empirical time series. The results indicate that network-based features capture the information encoded in each of the time series models, resulting in high accuracy in a clustering task. Our results are promising and show that network analysis can be used to characterize different types of time series and that different mapping methods capture different characteristics of the time series.