"Time Series Analysis": models, code, and papers
Robust Dominant Periodicity Detection for Time Series with Missing Data
Mar 06, 2023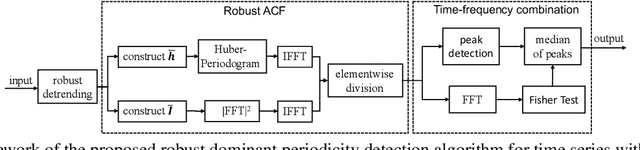
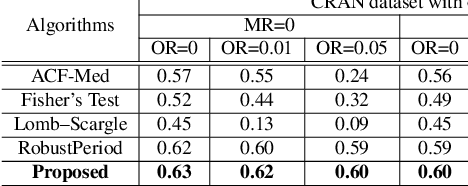
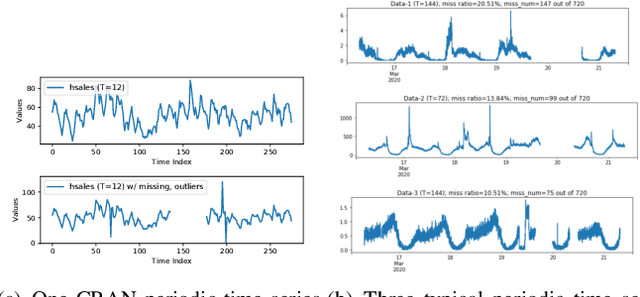
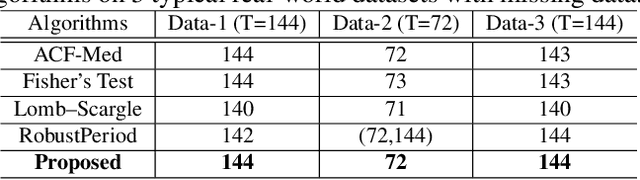
Periodicity detection is an important task in time series analysis, but still a challenging problem due to the diverse characteristics of time series data like abrupt trend change, outlier, noise, and especially block missing data. In this paper, we propose a robust and effective periodicity detection algorithm for time series with block missing data. We first design a robust trend filter to remove the interference of complicated trend patterns under missing data. Then, we propose a robust autocorrelation function (ACF) that can handle missing values and outliers effectively. We rigorously prove that the proposed robust ACF can still work well when the length of the missing block is less than $1/3$ of the period length. Last, by combining the time-frequency information, our algorithm can generate the period length accurately. The experimental results demonstrate that our algorithm outperforms existing periodicity detection algorithms on real-world time series datasets.
* Accepted by 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2023)
Global Outliers Detection in Wireless Sensor Networks: A Novel Approach Integrating Time-Series Analysis, Entropy, and Random Forest-based Classification
Jul 21, 2021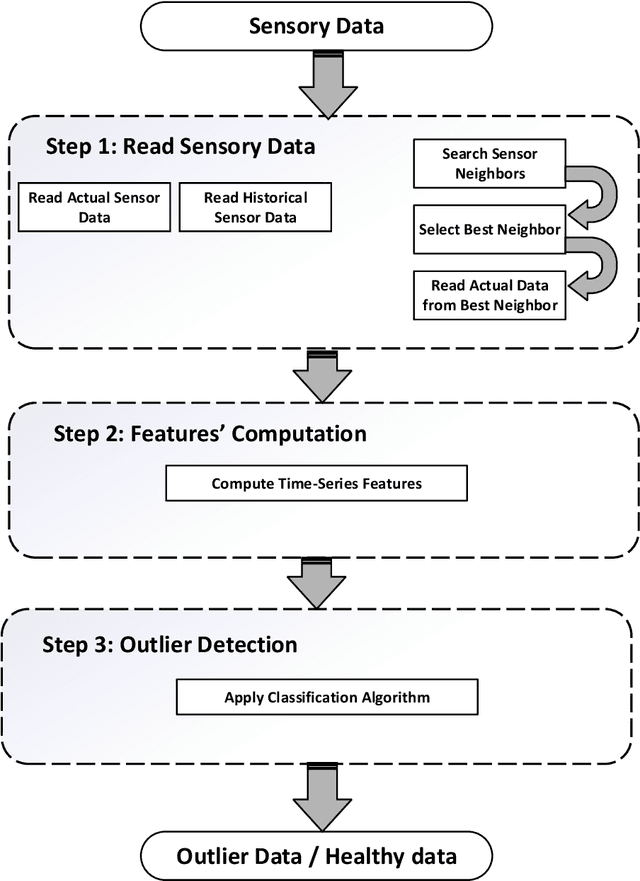
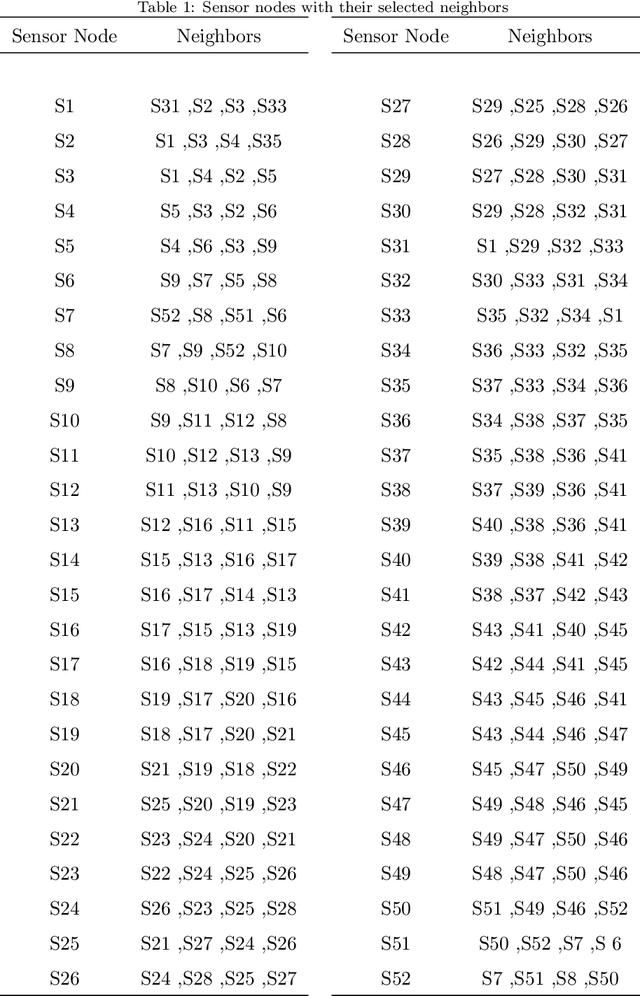
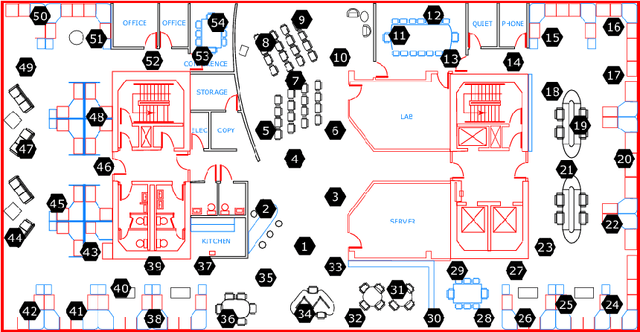
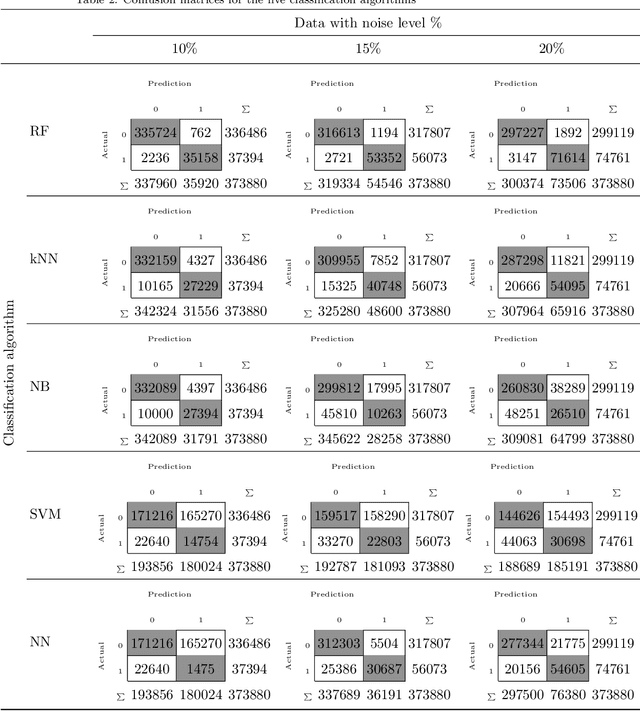
Wireless Sensor Networks (WSNs) have recently attracted greater attention worldwide due to their practicality in monitoring, communicating, and reporting specific physical phenomena. The data collected by WSNs is often inaccurate as a result of unavoidable environmental factors, which may include noise, signal weakness, or intrusion attacks depending on the specific situation. Sending high-noise data has negative effects not just on data accuracy and network reliability, but also regarding the decision-making processes in the base station. Anomaly detection, or outlier detection, is the process of detecting noisy data amidst the contexts thus described. The literature contains relatively few noise detection techniques in the context of WSNs, particularly for outlier-detection algorithms applying time series analysis, which considers the effective neighbors to ensure a global-collaborative detection. Hence, the research presented in this paper is intended to design and implement a global outlier-detection approach, which allows us to find and select appropriate neighbors to ensure an adaptive collaborative detection based on time-series analysis and entropy techniques. The proposed approach applies a random forest algorithm for identifying the best results. To measure the effectiveness and efficiency of the proposed approach, a comprehensive and real scenario provided by the Intel Berkeley Research lab has been simulated. Noisy data have been injected into the collected data randomly. The results obtained from the experiment then conducted experimentation demonstrate that our approach can detect anomalies with up to 99% accuracy.
Deep Learning for Time Series Classification and Extrinsic Regression: A Current Survey
Feb 06, 2023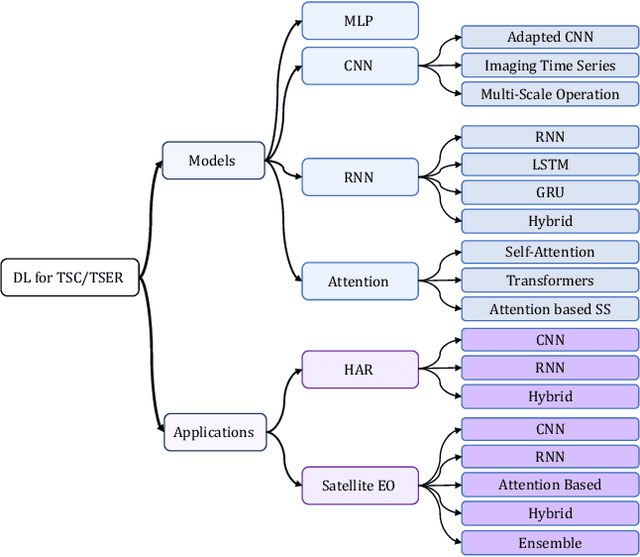
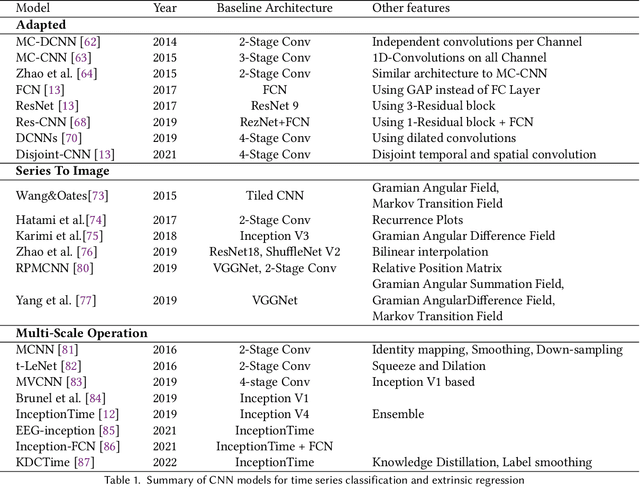
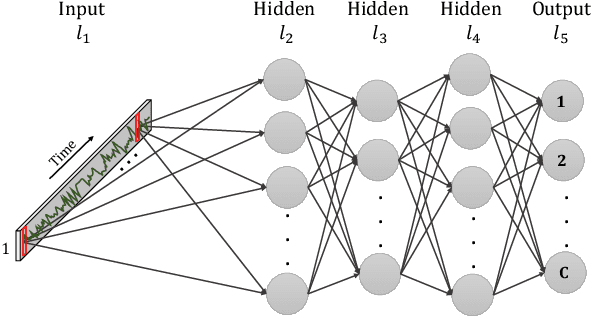
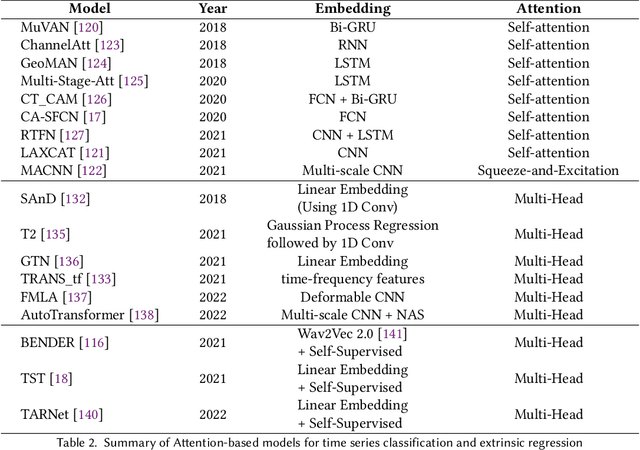
Time Series Classification and Extrinsic Regression are important and challenging machine learning tasks. Deep learning has revolutionized natural language processing and computer vision and holds great promise in other fields such as time series analysis where the relevant features must often be abstracted from the raw data but are not known a priori. This paper surveys the current state of the art in the fast-moving field of deep learning for time series classification and extrinsic regression. We review different network architectures and training methods used for these tasks and discuss the challenges and opportunities when applying deep learning to time series data. We also summarize two critical applications of time series classification and extrinsic regression, human activity recognition and satellite earth observation.
Variable-lag Granger Causality for Time Series Analysis
Dec 18, 2019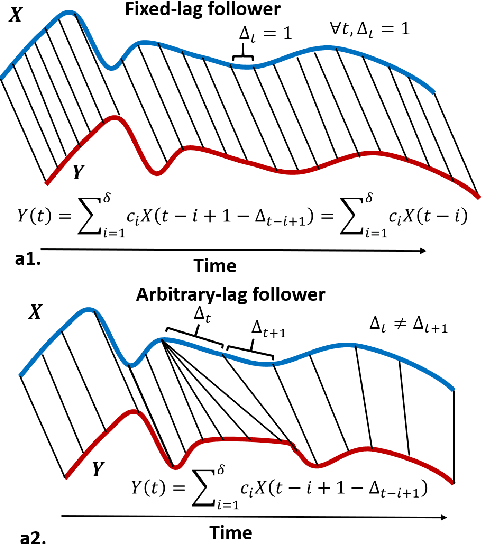
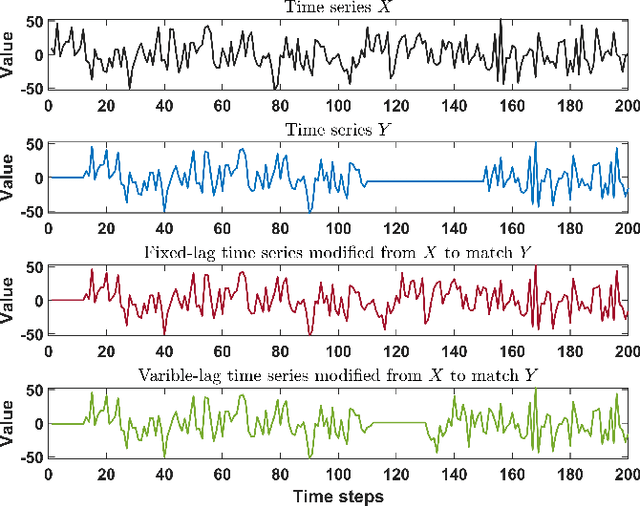
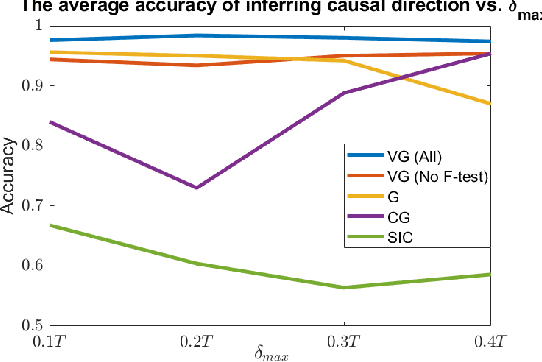
Granger causality is a fundamental technique for causal inference in time series data, commonly used in the social and biological sciences. Typical operationalizations of Granger causality make a strong assumption that every time point of the effect time series is influenced by a combination of other time series with a fixed time delay. However, the assumption of the fixed time delay does not hold in many applications, such as collective behavior, financial markets, and many natural phenomena. To address this issue, we develop variable-lag Granger causality, a generalization of Granger causality that relaxes the assumption of the fixed time delay and allows causes to influence effects with arbitrary time delays. In addition, we propose a method for inferring variable-lag Granger causality relations. We demonstrate our approach on an application for studying coordinated collective behavior and show that it performs better than several existing methods in both simulated and real-world datasets. Our approach can be applied in any domain of time series analysis.
A walk through of time series analysis on quantum computers
May 02, 2022
Because of the rotational components on quantum circuits, some quantum neural networks based on variational circuits can be considered equivalent to the classical Fourier networks. In addition, they can be used to predict Fourier coefficients of continuous functions. Time series data indicates a state of a variable in time. Since some time series data can be also considered as continuous functions, we can expect quantum machine learning models to do do many data analysis tasks successfully on time series data. Therefore, it is important to investigate new quantum logics for temporal data processing and analyze intrinsic relationships of data on quantum computers. In this paper, we go through the quantum analogues of classical data preprocessing and forecasting with ARIMA models by using simple quantum operators requiring a few number of quantum gates. Then we discuss future directions and some of the tools/algorithms that can be used for temporal data analysis on quantum computers.
FrAug: Frequency Domain Augmentation for Time Series Forecasting
Feb 18, 2023
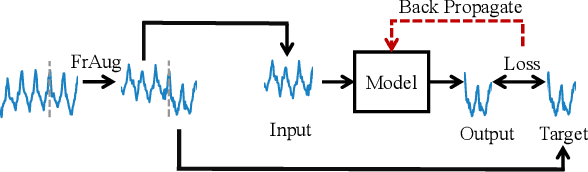
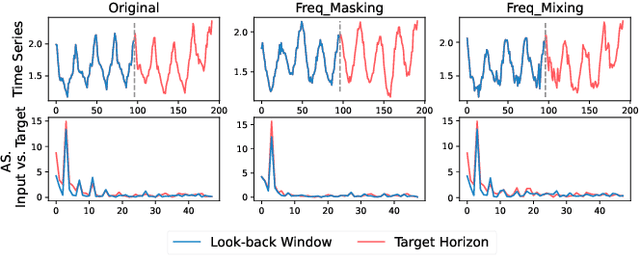

Data augmentation (DA) has become a de facto solution to expand training data size for deep learning. With the proliferation of deep models for time series analysis, various time series DA techniques are proposed in the literature, e.g., cropping-, warping-, flipping-, and mixup-based methods. However, these augmentation methods mainly apply to time series classification and anomaly detection tasks. In time series forecasting (TSF), we need to model the fine-grained temporal relationship within time series segments to generate accurate forecasting results given data in a look-back window. Existing DA solutions in the time domain would break such a relationship, leading to poor forecasting accuracy. To tackle this problem, this paper proposes simple yet effective frequency domain augmentation techniques that ensure the semantic consistency of augmented data-label pairs in forecasting, named FrAug. We conduct extensive experiments on eight widely-used benchmarks with several state-of-the-art TSF deep models. Our results show that FrAug can boost the forecasting accuracy of TSF models in most cases. Moreover, we show that FrAug enables models trained with 1\% of the original training data to achieve similar performance to the ones trained on full training data, which is particularly attractive for cold-start forecasting. Finally, we show that applying test-time training with FrAug greatly improves forecasting accuracy for time series with significant distribution shifts, which often occurs in real-life TSF applications. Our code is available at https://anonymous.4open.science/r/Fraug-more-results-1785.
Mobile Mapping Mesh Change Detection and Update
Mar 13, 2023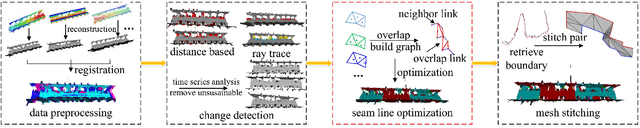
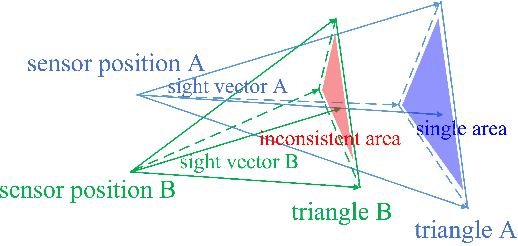
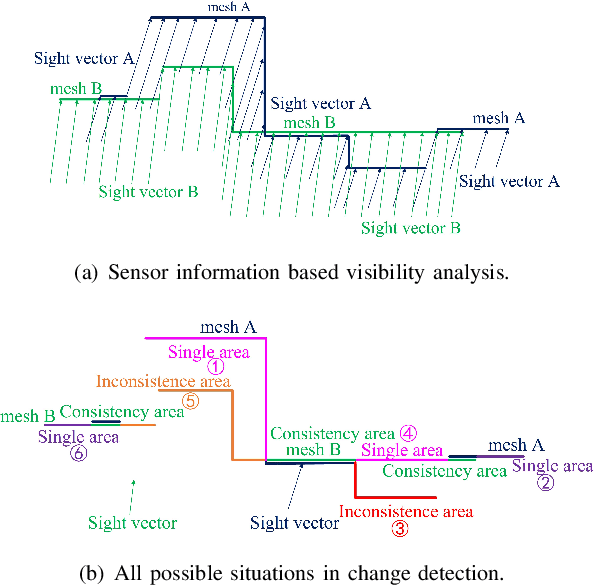

Mobile mapping, in particular, Mobile Lidar Scanning (MLS) is increasingly widespread to monitor and map urban scenes at city scale with unprecedented resolution and accuracy. The resulting point cloud sampling of the scene geometry can be meshed in order to create a continuous representation for different applications: visualization, simulation, navigation, etc. Because of the highly dynamic nature of these urban scenes, long term mapping should rely on frequent map updates. A trivial solution is to simply replace old data with newer data each time a new acquisition is made. However it has two drawbacks: 1) the old data may be of higher quality (resolution, precision) than the new and 2) the coverage of the scene might be different in various acquisitions, including varying occlusions. In this paper, we propose a fully automatic pipeline to address these two issues by formulating the problem of merging meshes with different quality, coverage and acquisition time. Our method is based on a combined distance and visibility based change detection, a time series analysis to assess the sustainability of changes, a mesh mosaicking based on a global boolean optimization and finally a stitching of the resulting mesh pieces boundaries with triangle strips. Finally, our method is demonstrated on Robotcar and Stereopolis datasets.
What Constitutes Good Contrastive Learning in Time-Series Forecasting?
Jun 21, 2023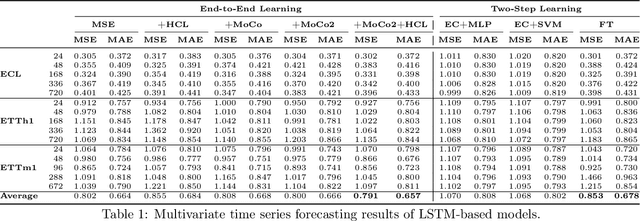
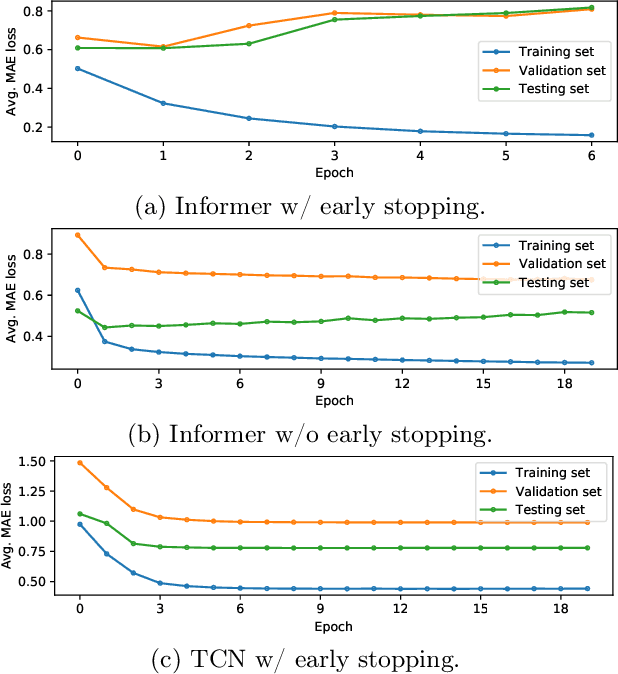
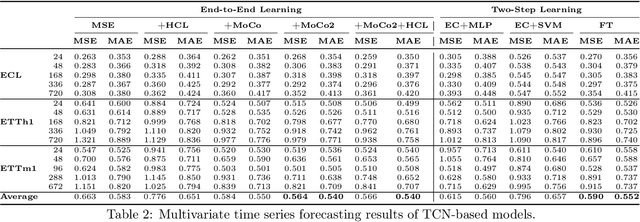
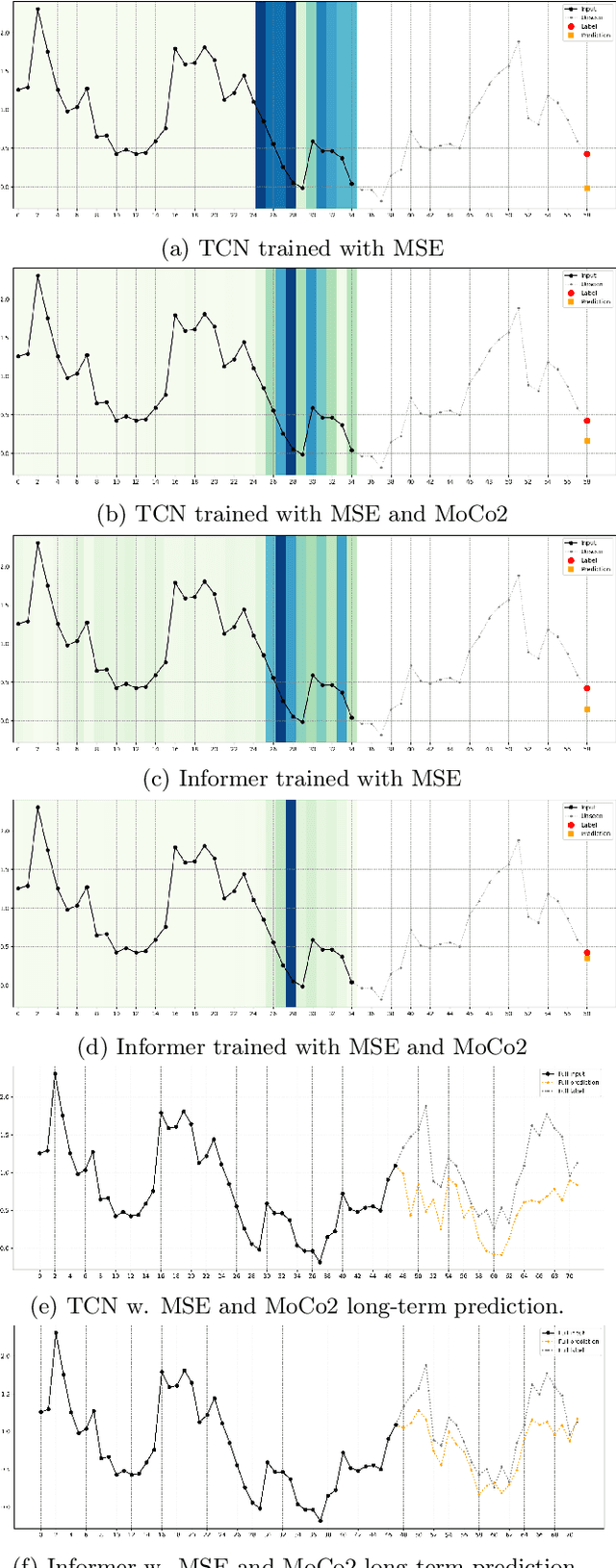
In recent years, the introduction of self-supervised contrastive learning (SSCL) has demonstrated remarkable improvements in representation learning across various domains, including natural language processing and computer vision. By leveraging the inherent benefits of self-supervision, SSCL enables the pre-training of representation models using vast amounts of unlabeled data. Despite these advances, there remains a significant gap in understanding the impact of different SSCL strategies on time series forecasting performance, as well as the specific benefits that SSCL can bring. This paper aims to address these gaps by conducting a comprehensive analysis of the effectiveness of various training variables, including different SSCL algorithms, learning strategies, model architectures, and their interplay. Additionally, to gain deeper insights into the improvements brought about by SSCL in the context of time-series forecasting, a qualitative analysis of the empirical receptive field is performed. Through our experiments, we demonstrate that the end-to-end training of a Transformer model using the Mean Squared Error (MSE) loss and SSCL emerges as the most effective approach in time series forecasting. Notably, the incorporation of the contrastive objective enables the model to prioritize more pertinent information for forecasting, such as scale and periodic relationships. These findings contribute to a better understanding of the benefits of SSCL in time series forecasting and provide valuable insights for future research in this area.
Deep Discriminative Direct Decoders for High-dimensional Time-series Analysis
May 22, 2022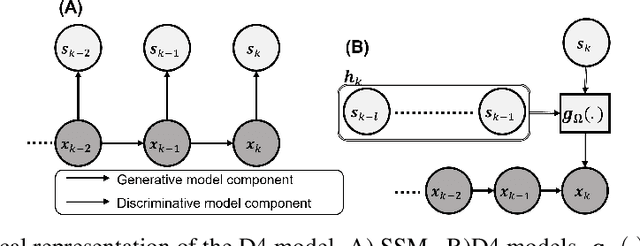
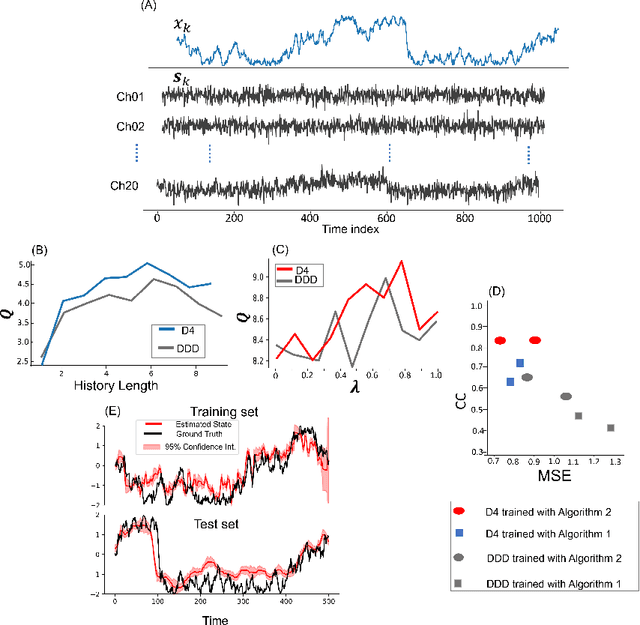
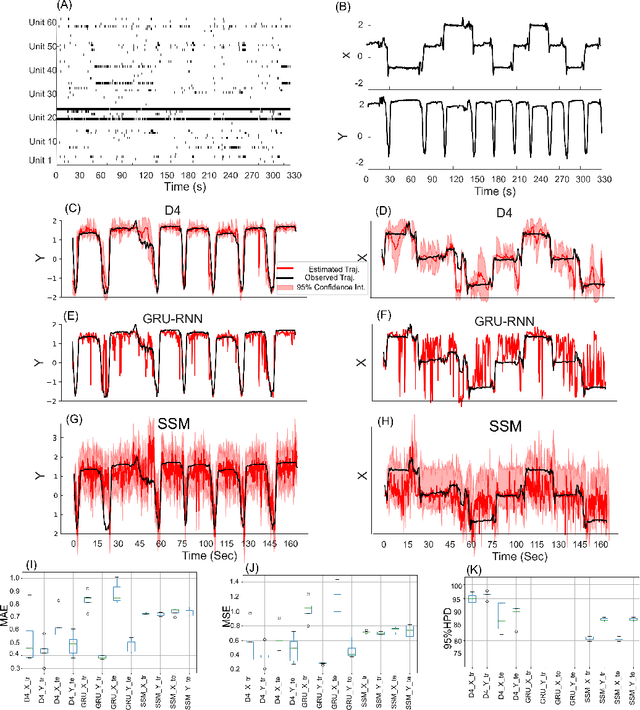
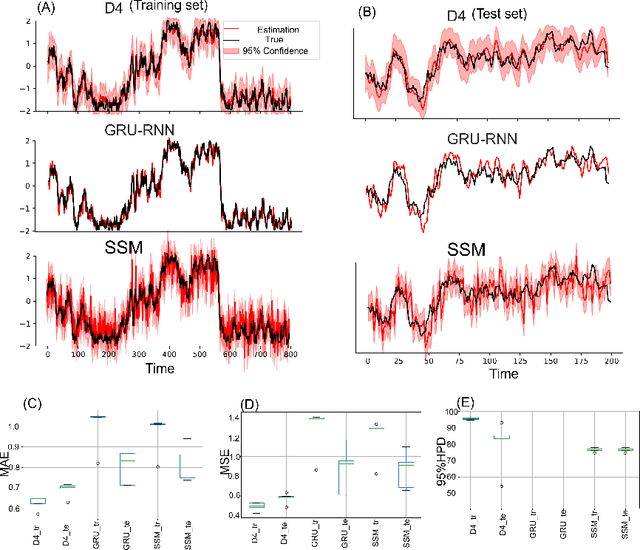
Dynamical latent variable modeling has been significantly invested over the last couple of decades with established solutions encompassing generative processes like the state-space model (SSM) and discriminative processes like a recurrent or a deep neural network (DNN). These solutions are powerful tools with promising results; however, surprisingly they were never put together in a unified model to analyze complex multivariate time-series data. A very recent modeling approach, called the direct discriminative decoder (DDD) model, proposes a principal solution to combine SMM and DNN models, with promising results in decoding underlying latent processes, e.g. rat movement trajectory, through high-dimensional neural recordings. The DDD consists of a) a state transition process, as per the classical dynamical models, and b) a discriminative process, like DNN, in which the conditional distribution of states is defined as a function of the current observations and their recent history. Despite promising results of the DDD model, no training solutions, in the context of DNN, have been utilized for this model. Here, we propose how DNN parameters along with an optimal history term can be simultaneously estimated as a part of the DDD model. We use the D4 abbreviation for a DDD with a DNN as its discriminative process. We showed the D4 decoding performance in both simulation and (relatively) high-dimensional neural data. In both datasets, D4 performance surpasses the state-of-art decoding solutions, including those of SSM and DNNs. The key success of DDD and potentially D4 is efficient utilization of the recent history of observation along with the state-process that carries long-term information, which is not addressed in either SSM or DNN solutions. We argue that D4 can be a powerful tool for the analysis of high-dimensional time-series data.
Visual Explanations with Attributions and Counterfactuals on Time Series Classification
Jul 14, 2023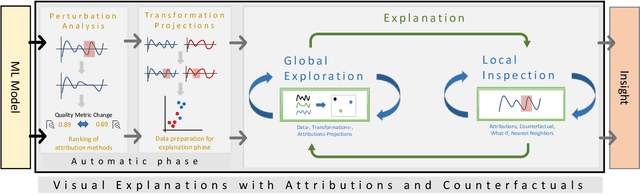
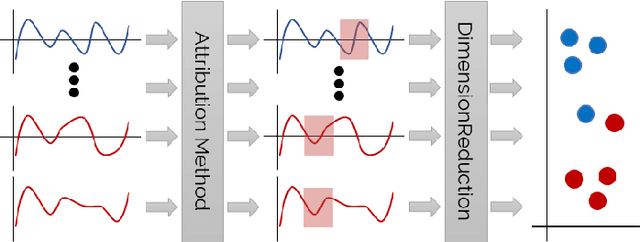
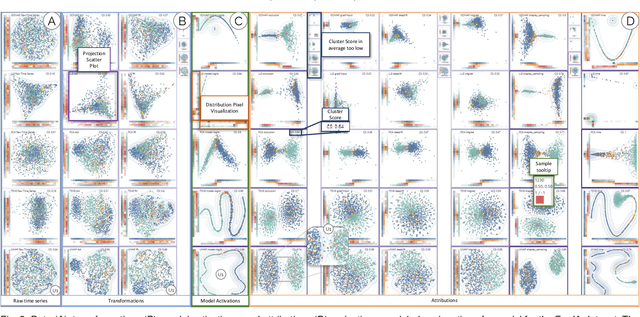
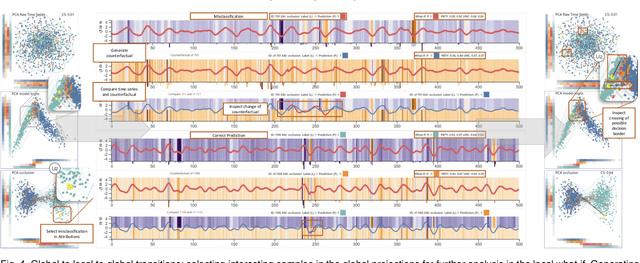
With the rising necessity of explainable artificial intelligence (XAI), we see an increase in task-dependent XAI methods on varying abstraction levels. XAI techniques on a global level explain model behavior and on a local level explain sample predictions. We propose a visual analytics workflow to support seamless transitions between global and local explanations, focusing on attributions and counterfactuals on time series classification. In particular, we adapt local XAI techniques (attributions) that are developed for traditional datasets (images, text) to analyze time series classification, a data type that is typically less intelligible to humans. To generate a global overview, we apply local attribution methods to the data, creating explanations for the whole dataset. These explanations are projected onto two dimensions, depicting model behavior trends, strategies, and decision boundaries. To further inspect the model decision-making as well as potential data errors, a what-if analysis facilitates hypothesis generation and verification on both the global and local levels. We constantly collected and incorporated expert user feedback, as well as insights based on their domain knowledge, resulting in a tailored analysis workflow and system that tightly integrates time series transformations into explanations. Lastly, we present three use cases, verifying that our technique enables users to (1)~explore data transformations and feature relevance, (2)~identify model behavior and decision boundaries, as well as, (3)~the reason for misclassifications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge