Counterfactual Basis Extension and Representational Geometry: An MDL-Constrained Model of Conceptual Growth

Concept learning becomes possible only when existing representations fail to account for experience. Most models of learning and inference, however, presuppose a fixed representational basis within which belief updating occurs. In this paper, I address a prior question: under what structural conditions can the representational basis itself expand in a principled and selective way? I propose a geometric framework in which conceptual growth is modeled as admissible basis extension evaluated under a Minimum Description Length (MDL) criterion. Experience, whether externally observed or internally simulated, is represented as vectors relative to a current conceptual subspace. Residual components capture systematic representational failure, and candidate conceptual extensions are restricted to low-rank, admissible transformations. I show that any MDL-accepted extension can be chosen so that its novel directions lie entirely within the residual span induced by experience, while extensions orthogonal to this span strictly increase description length and are therefore rejected. This yields a conservative account of imagination and conceptual innovation. Internally generated counterfactual representations contribute to learning only insofar as they expose or amplify structured residual error, and cannot introduce arbitrary novelty. I further distinguish representational counterfactuals--counterfactuals over an agent's conceptual basis--from causal or value-level counterfactuals, and show how MDL provides a normative selection principle governing representational change. Overall, the framework characterizes conceptual development as an error-driven, geometry-constrained process of basis extension, clarifying both the role and the limits of imagination in learning and theory change.

Interpretation as Linear Transformation: A Cognitive-Geometric Model of Belief and Meaning

This paper develops a geometric framework for modeling belief, motivation, and influence across cognitively heterogeneous agents. Each agent is represented by a personalized value space, a vector space encoding the internal dimensions through which the agent interprets and evaluates meaning. Beliefs are formalized as structured vectors-abstract beings-whose transmission is mediated by linear interpretation maps. A belief survives communication only if it avoids the null spaces of these maps, yielding a structural criterion for intelligibility, miscommunication, and belief death. Within this framework, I show how belief distortion, motivational drift, counterfactual evaluation, and the limits of mutual understanding arise from purely algebraic constraints. A central result-"the No-Null-Space Leadership Condition"-characterizes leadership as a property of representational reachability rather than persuasion or authority. More broadly, the model explains how abstract beings can propagate, mutate, or disappear as they traverse diverse cognitive geometries. The account unifies insights from conceptual spaces, social epistemology, and AI value alignment by grounding meaning preservation in structural compatibility rather than shared information or rationality. I argue that this cognitive-geometric perspective clarifies the epistemic boundaries of influence in both human and artificial systems, and offers a general foundation for analyzing belief dynamics across heterogeneous agents.

Multi-Band Variable-Lag Granger Causality: A Unified Framework for Causal Time Series Inference across Frequencies

Understanding causal relationships in time series is fundamental to many domains, including neuroscience, economics, and behavioral science. Granger causality is one of the well-known techniques for inferring causality in time series. Typically, Granger causality frameworks have a strong fix-lag assumption between cause and effect, which is often unrealistic in complex systems. While recent work on variable-lag Granger causality (VLGC) addresses this limitation by allowing a cause to influence an effect with different time lags at each time point, it fails to account for the fact that causal interactions may vary not only in time delay but also across frequency bands. For example, in brain signals, alpha-band activity may influence another region with a shorter delay than slower delta-band oscillations. In this work, we formalize Multi-Band Variable-Lag Granger Causality (MB-VLGC) and propose a novel framework that generalizes traditional VLGC by explicitly modeling frequency-dependent causal delays. We provide a formal definition of MB-VLGC, demonstrate its theoretical soundness, and propose an efficient inference pipeline. Extensive experiments across multiple domains demonstrate that our framework significantly outperforms existing methods on both synthetic and real-world datasets, confirming its broad applicability to any type of time series data. Code and datasets are publicly available.

Inferring the Most Similar Variable-length Subsequences between Multidimensional Time Series

Finding the most similar subsequences between two multidimensional time series has many applications: e.g. capturing dependency in stock market or discovering coordinated movement of baboons. Considering one pattern occurring in one time series, we might be wondering whether the same pattern occurs in another time series with some distortion that might have a different length. Nevertheless, to the best of our knowledge, there is no efficient framework that deals with this problem yet. In this work, we propose an algorithm that provides the exact solution of finding the most similar multidimensional subsequences between time series where there is a difference in length both between time series and between subsequences. The algorithm is built based on theoretical guarantee of correctness and efficiency. The result in simulation datasets illustrated that our approach not just only provided correct solution, but it also utilized running time only quarter of time compared against the baseline approaches. In real-world datasets, it extracted the most similar subsequences even faster (up to 20 times faster against baseline methods) and provided insights regarding the situation in stock market and following relations of multidimensional time series of baboon movement. Our approach can be used for any time series. The code and datasets of this work are provided for the public use.

Some Insights of Construction of Feature Graph to Learn Pairwise Feature Interactions with Graph Neural Networks

Feature interaction is crucial in predictive machine learning models, as it captures the relationships between features that influence model performance. In this work, we focus on pairwise interactions and investigate their importance in constructing feature graphs for Graph Neural Networks (GNNs). Rather than proposing new methods, we leverage existing GNN models and tools to explore the relationship between feature graph structures and their effectiveness in modeling interactions. Through experiments on synthesized datasets, we uncover that edges between interacting features are important for enabling GNNs to model feature interactions effectively. We also observe that including non-interaction edges can act as noise, degrading model performance. Furthermore, we provide theoretical support for sparse feature graph selection using the Minimum Description Length (MDL) principle. We prove that feature graphs retaining only necessary interaction edges yield a more efficient and interpretable representation than complete graphs, aligning with Occam's Razor. Our findings offer both theoretical insights and practical guidelines for designing feature graphs that improve the performance and interpretability of GNN models.

Framework for Variable-lag Motif Following Relation Inference In Time Series using Matrix Profile analysis

Knowing who follows whom and what patterns they are following are crucial steps to understand collective behaviors (e.g. a group of human, a school of fish, or a stock market). Time series is one of resources that can be used to get insight regarding following relations. However, the concept of following patterns or motifs and the solution to find them in time series are not obvious. In this work, we formalize a concept of following motifs between two time series and present a framework to infer following patterns between two time series. The framework utilizes one of efficient and scalable methods to retrieve motifs from time series called the Matrix Profile Method. We compare our proposed framework with several baselines. The framework performs better than baselines in the simulation datasets. In the dataset of sound recording, the framework is able to retrieve the following motifs within a pair of time series that two singers sing following each other. In the cryptocurrency dataset, the framework is capable of capturing the following motifs within a pair of time series from two digital currencies, which implies that the values of one currency follow the values of another currency patterns. Our framework can be utilized in any field of time series to get insight regarding following patterns between time series.

Framework for inferring empirical causal graphs from binary data to support multidimensional poverty analysis

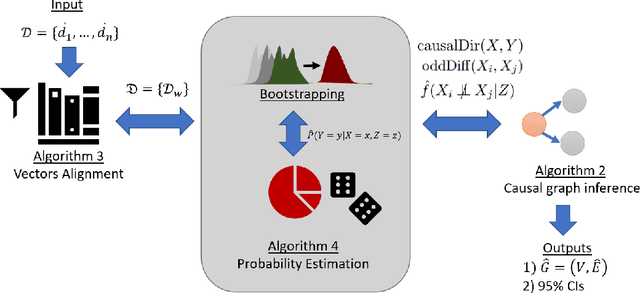
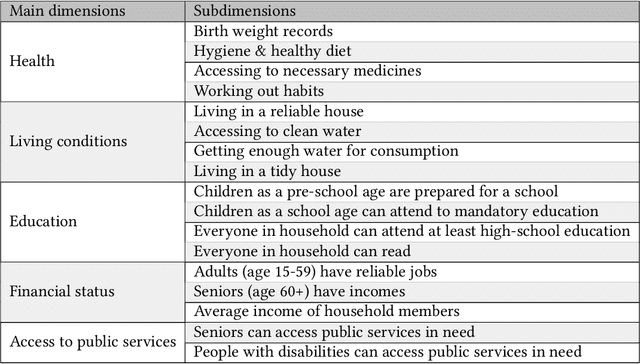
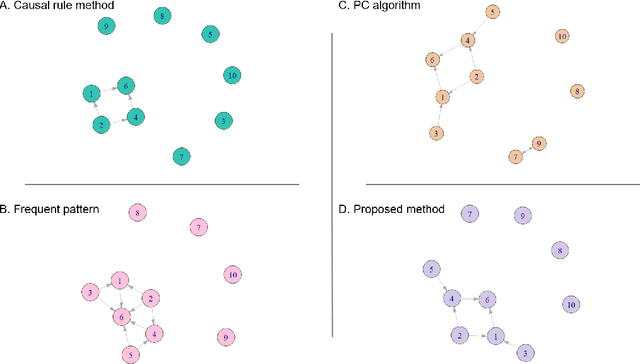
Poverty is one of the fundamental issues that mankind faces. Multidimensional Poverty Index (MPI) is deployed for measuring poverty issues in a population beyond monetary. However, MPI cannot provide information regarding associations and causal relations among poverty factors. Does education cause income inequality in a specific region? Is lacking education a cause of health issues? By not knowing causal relations, policy maker cannot pinpoint root causes of poverty issues of a specific population, which might not be the same across different population. Additionally, MPI requires binary data, which cannot be analyzed by most of causal inference frameworks. In this work, we proposed an exploratory-data-analysis framework for finding possible causal relations with confidence intervals among binary data. The proposed framework provides not only how severe the issue of poverty is, but it also provides the causal relations among poverty factors. Moreover, knowing a confidence interval of degree of causal direction lets us know how strong a causal relation is. We evaluated the proposed framework with several baseline approaches in simulation datasets as well as using two real-world datasets as case studies 1) Twin births of the United States: the relation between birth weight and mortality of twin, and 2) Thailand population surveys from 378k households of Chiang Mai and 353k households of Khon Kaen provinces. Our framework performed better than baselines in most cases. The first case study reveals almost all mortality cases in twins have issues of low birth weights but not all low-birth-weight twins were died. The second case study reveals that smoking associates with drinking alcohol in both provinces and there is a causal relation of smoking causes drinking alcohol in only Chiang Mai province. The framework can be applied beyond the poverty context.

Mining and modeling complex leadership-followership dynamics of movement data

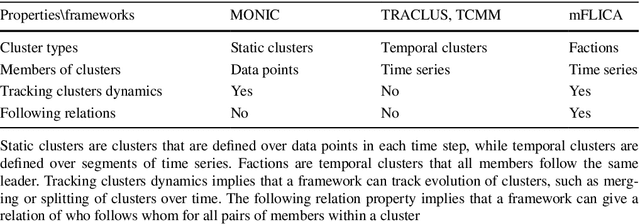
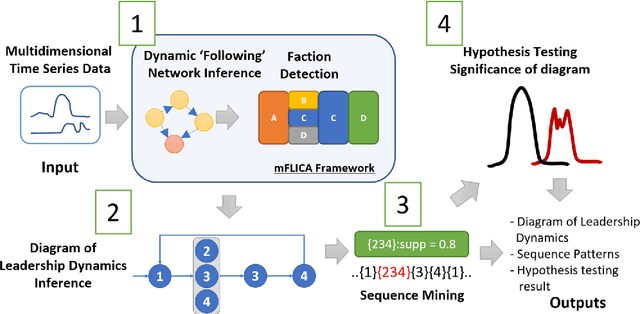
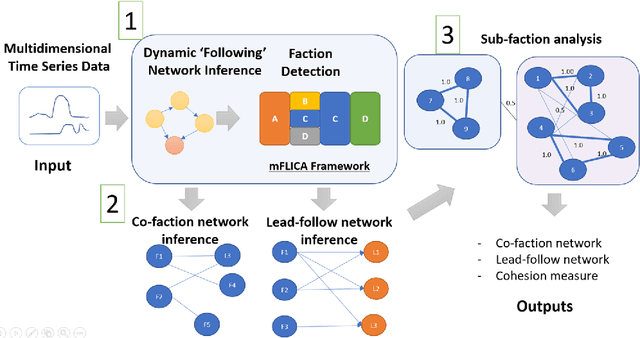
Leadership and followership are essential parts of collective decision and organization in social animals, including humans. In nature, relationships of leaders and followers are dynamic and vary with context or temporal factors. Understanding dynamics of leadership and followership, such as how leaders and followers change, emerge, or converge, allows scientists to gain more insight into group decision-making and collective behavior in general. However, given only data of individual activities, it is challenging to infer the dynamics of leaders and followers. In this paper, we focus on mining and modeling frequent patterns of leading and following. We formalize new computational problems and propose a framework that can be used to address several questions regarding group movement. We use the leadership inference framework, mFLICA, to infer the time series of leaders and their factions from movement datasets and then propose an approach to mine and model frequent patterns of both leadership and followership dynamics. We evaluate our framework performance by using several simulated datasets, as well as the real-world dataset of baboon movement to demonstrate the applications of our framework. These are novel computational problems and, to the best of our knowledge, there are no existing comparable methods to address them. Thus, we modify and extend an existing leadership inference framework to provide a non-trivial baseline for comparison. Our framework performs better than this baseline in all datasets. Our framework opens the opportunities for scientists to generate testable scientific hypotheses about the dynamics of leadership in movement data.

Variable-lag Granger Causality and Transfer Entropy for Time Series Analysis

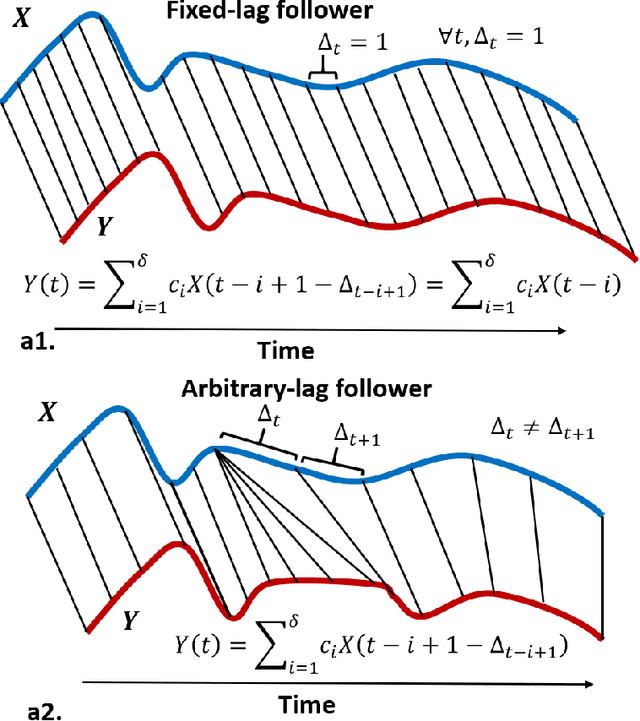
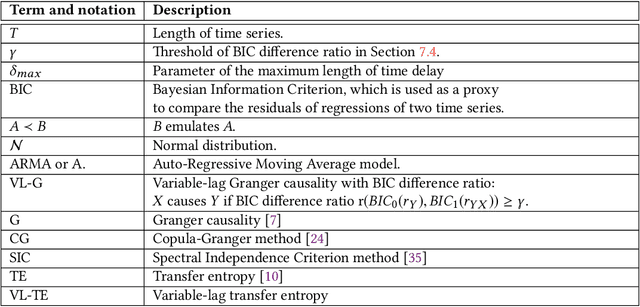
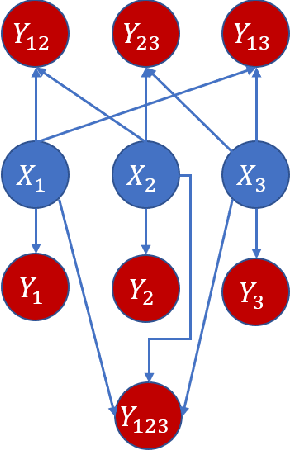
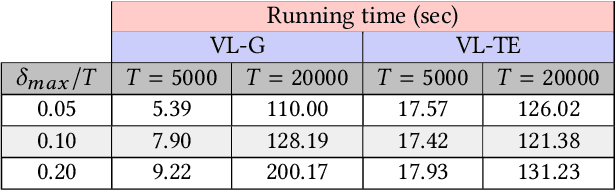
Granger causality is a fundamental technique for causal inference in time series data, commonly used in the social and biological sciences. Typical operationalizations of Granger causality make a strong assumption that every time point of the effect time series is influenced by a combination of other time series with a fixed time delay. The assumption of fixed time delay also exists in Transfer Entropy, which is considered to be a non-linear version of Granger causality. However, the assumption of the fixed time delay does not hold in many applications, such as collective behavior, financial markets, and many natural phenomena. To address this issue, we develop Variable-lag Granger causality and Variable-lag Transfer Entropy, generalizations of both Granger causality and Transfer Entropy that relax the assumption of the fixed time delay and allow causes to influence effects with arbitrary time delays. In addition, we propose a method for inferring both variable-lag Granger causality and Transfer Entropy relations. We demonstrate our approaches on an application for studying coordinated collective behavior and other real-world casual-inference datasets and show that our proposed approaches perform better than several existing methods in both simulated and real-world datasets. Our approaches can be applied in any domain of time series analysis. The software of this work is available in the R-CRAN package: VLTimeCausality.

Variable-lag Granger Causality for Time Series Analysis

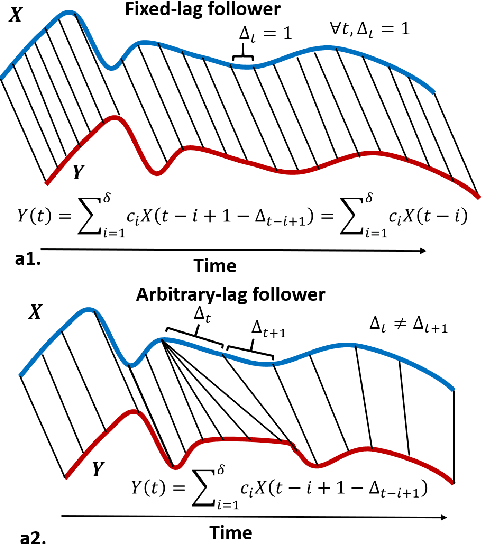
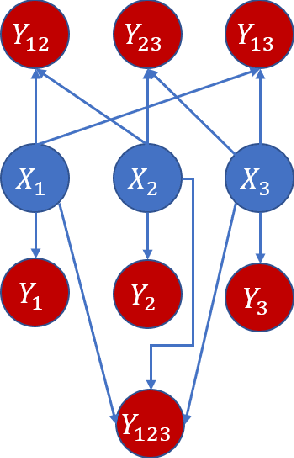
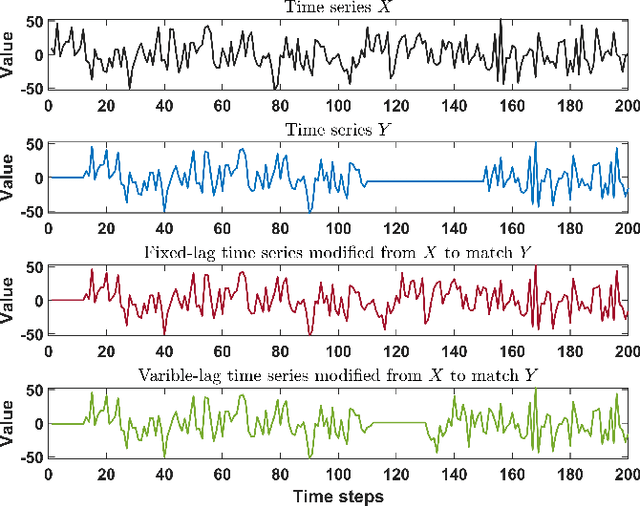
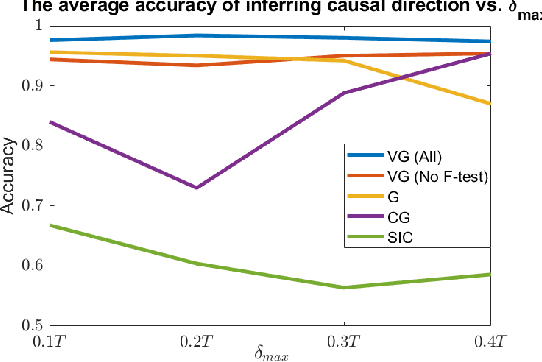
Granger causality is a fundamental technique for causal inference in time series data, commonly used in the social and biological sciences. Typical operationalizations of Granger causality make a strong assumption that every time point of the effect time series is influenced by a combination of other time series with a fixed time delay. However, the assumption of the fixed time delay does not hold in many applications, such as collective behavior, financial markets, and many natural phenomena. To address this issue, we develop variable-lag Granger causality, a generalization of Granger causality that relaxes the assumption of the fixed time delay and allows causes to influence effects with arbitrary time delays. In addition, we propose a method for inferring variable-lag Granger causality relations. We demonstrate our approach on an application for studying coordinated collective behavior and show that it performs better than several existing methods in both simulated and real-world datasets. Our approach can be applied in any domain of time series analysis.