Dimension reduction with structure-aware quantum circuits for hybrid machine learning

Schmidt decomposition of a vector can be understood as writing the singular value decomposition (SVD) in vector form. A vector can be written as a linear combination of tensor product of two dimensional vectors by recursively applying Schmidt decompositions via SVD to all subsystems. Given a vector expressed as a linear combination of tensor products, using only the $k$ principal terms yields a $k$-rank approximation of the vector. Therefore, writing a vector in this reduced form allows to retain most important parts of the vector while removing small noises from it, analogous to SVD-based denoising. In this paper, we show that quantum circuits designed based on a value $k$ (determined from the tensor network decomposition of the mean vector of the training sample) can approximate the reduced-form representations of entire datasets. We then employ this circuit ansatz with a classical neural network head to construct a hybrid machine learning model. Since the output of the quantum circuit for an $2^n$ dimensional vector is an $n$ dimensional probability vector, this provides an exponential compression of the input and potentially can reduce the number of learnable parameters for training large-scale models. We use datasets provided in the Python scikit-learn module for the experiments. The results confirm the quantum circuit is able to compress data successfully to provide effective $k$-rank approximations to the classical processing component.

Quantum RNNs and LSTMs Through Entangling and Disentangling Power of Unitary Transformations

In this paper, we discuss how quantum recurrent neural networks (RNNs) and their enhanced version, long short-term memory (LSTM) networks, can be modeled using the core ideas presented in Ref.[1], where the entangling and disentangling power of unitary transformations is investigated. In particular, we interpret entangling and disentangling power as information retention and forgetting mechanisms in LSTMs. Therefore, entanglement becomes a key component of the optimization (training) process. We believe that, by leveraging prior knowledge of the entangling power of unitaries, the proposed quantum-classical framework can guide and help to design better-parameterized quantum circuits for various real-world applications.

Quantum Kolmogorov-Arnold networks by combining quantum signal processing circuits

In this paper, we show that an equivalent implementation of KAN can be done on quantum computers by simply combining quantum signal processing circuits in layers. This provides a powerful and robust path for the applications of KAN on quantum computers.

A unifying primary framework for quantum graph neural networks from quantum graph states

Graph states are used to represent mathematical graphs as quantum states on quantum computers. They can be formulated through stabilizer codes or directly quantum gates and quantum states. In this paper we show that a quantum graph neural network model can be understood and realized based on graph states. We show that they can be used either as a parameterized quantum circuits to represent neural networks or as an underlying structure to construct graph neural networks on quantum computers.

Federated learning with distributed fixed design quantum chips and quantum channels

The privacy in classical federated learning can be breached through the use of local gradient results along with engineered queries to the clients. However, quantum communication channels are considered more secure because a measurement on the channel causes a loss of information, which can be detected by the sender. Therefore, the quantum version of federated learning can be used to provide more privacy. Additionally, sending an $N$ dimensional data vector through a quantum channel requires sending $\log N$ entangled qubits, which can potentially provide exponential efficiency if the data vector is utilized as quantum states. In this paper, we propose a quantum federated learning model where fixed design quantum chips are operated based on the quantum states sent by a centralized server. Based on the coming superposition states, the clients compute and then send their local gradients as quantum states to the server, where they are aggregated to update parameters. Since the server does not send model parameters, but instead sends the operator as a quantum state, the clients are not required to share the model. This allows for the creation of asynchronous learning models. In addition, the model as a quantum state is fed into client-side chips directly; therefore, it does not require measurements on the upcoming quantum state to obtain model parameters in order to compute gradients. This can provide efficiency over the models where the parameter vector is sent via classical or quantum channels and local gradients are obtained through the obtained values of these parameters.

A Simple Quantum Blockmodeling with Qubits and Permutations

Blockmodeling of a given problem represented by an $N\times N$ adjacency matrix can be found by swapping rows and columns of the matrix (i.e. multiplying matrix from left and right by a permutation matrix). In general, through performing this task, row and column permutations affect the fitness value in optimization: For an $N\times N$ matrix, it requires $O(N)$ computations to find (or update) the fitness value of a candidate solution. On quantum computers, permutations can be applied in parallel and efficiently, and their implementations can be as simple as a single qubit operation (a NOT gate on a qubit) which takes an $O(1)$ time algorithmic step. In this paper, using permutation matrices, we describe a quantum blockmodeling for data analysis tasks. In the model, the measurement outcome of a small group of qubits are mapped to indicate the fitness value. Therefore, we show that it is possible to find or update the fitness value in $O(log(N))$ time. This lead us to show that when the number of iterations are less than $log(N)$ time, it may be possible to reach the same solution exponentially faster on quantum computers in comparison to classical computers. In addition, since on quantum circuits the different sequence of permutations can be applied in parallel (superpositon), the machine learning task in this model can be implemented more efficiently on quantum computers.

Dimension reduction and redundancy removal through successive Schmidt decompositions

Quantum computers are believed to have the ability to process huge data sizes which can be seen in machine learning applications. In these applications, the data in general is classical. Therefore, to process them on a quantum computer, there is a need for efficient methods which can be used to map classical data on quantum states in a concise manner. On the other hand, to verify the results of quantum computers and study quantum algorithms, we need to be able to approximate quantum operations into forms that are easier to simulate on classical computers with some errors. Motivated by these needs, in this paper we study the approximation of matrices and vectors by using their tensor products obtained through successive Schmidt decompositions. We show that data with distributions such as uniform, Poisson, exponential, or similar to these distributions can be approximated by using only a few terms which can be easily mapped onto quantum circuits. The examples include random data with different distributions, the Gram matrices of iris flower, handwritten digits, 20newsgroup, and labeled faces in the wild. And similarly, some quantum operations such as quantum Fourier transform and variational quantum circuits with a small depth also may be approximated with a few terms that are easier to simulate on classical computers. Furthermore, we show how the method can be used to simplify quantum Hamiltonians: In particular, we show the application to randomly generated transverse field Ising model Hamiltonians. The reduced Hamiltonians can be mapped into quantum circuits easily and therefore can be simulated more efficiently.

On the explainability of quantum neural networks based on variational quantum circuits

Ridge functions are used to describe and study the lower bound of the approximation done by the neural networks which can be written as a linear combination of activation functions. If the activation functions are also ridge functions, these networks are called explainable neural networks. In this paper, we first show that quantum neural networks which are based on variational quantum circuits can be written as a linear combination of ridge functions. Consequently, we show that the interpretability and explainability of such quantum neural networks can be directly considered and studied as an approximation with the linear combination of ridge functions.

A walk through of time series analysis on quantum computers

Because of the rotational components on quantum circuits, some quantum neural networks based on variational circuits can be considered equivalent to the classical Fourier networks. In addition, they can be used to predict Fourier coefficients of continuous functions. Time series data indicates a state of a variable in time. Since some time series data can be also considered as continuous functions, we can expect quantum machine learning models to do do many data analysis tasks successfully on time series data. Therefore, it is important to investigate new quantum logics for temporal data processing and analyze intrinsic relationships of data on quantum computers. In this paper, we go through the quantum analogues of classical data preprocessing and forecasting with ARIMA models by using simple quantum operators requiring a few number of quantum gates. Then we discuss future directions and some of the tools/algorithms that can be used for temporal data analysis on quantum computers.

A Generalized Circuit for the Hamiltonian Dynamics Through the Truncated Series

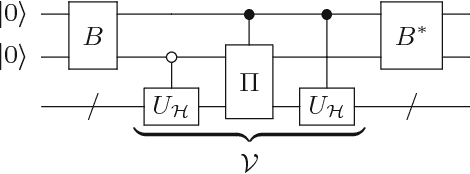
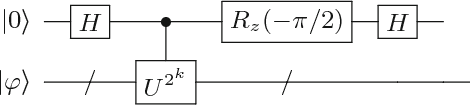
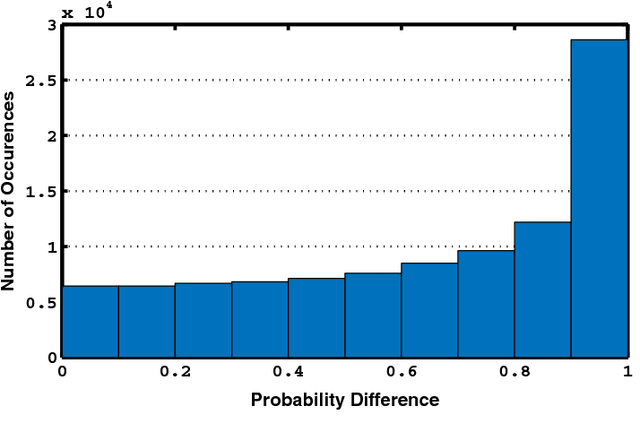
In this paper, we present a method for the Hamiltonian simulation in the context of eigenvalue estimation problems which improves earlier results dealing with Hamiltonian simulation through the truncated Taylor series. In particular, we present a fixed-quantum circuit design for the simulation of the Hamiltonian dynamics, $H(t)$, through the truncated Taylor series method described by Berry et al. \cite{berry2015simulating}. The circuit is general and can be used to simulate any given matrix in the phase estimation algorithm by only changing the angle values of the quantum gates implementing the time variable $t$ in the series. The circuit complexity depends on the number of summation terms composing the Hamiltonian and requires $O(Ln)$ number of quantum gates for the simulation of a molecular Hamiltonian. Here, $n$ is the number of states of a spin orbital, and $L$ is the number of terms in the molecular Hamiltonian and generally bounded by $O(n^4)$. We also discuss how to use the circuit in adaptive processes and eigenvalue related problems along with a slight modified version of the iterative phase estimation algorithm. In addition, a simple divide and conquer method is presented for mapping a matrix which are not given as sums of unitary matrices into the circuit. The complexity of the circuit is directly related to the structure of the matrix and can be bounded by $O(poly(n))$ for a matrix with $poly(n)-$sparsity.