Generative Modelling with High-Order Langevin Dynamics

Diffusion generative modelling (DGM) based on stochastic differential equations (SDEs) with score matching has achieved unprecedented results in data generation. In this paper, we propose a novel fast high-quality generative modelling method based on high-order Langevin dynamics (HOLD) with score matching. This motive is proved by third-order Langevin dynamics. By augmenting the previous SDEs, e.g. variance exploding or variance preserving SDEs for single-data variable processes, HOLD can simultaneously model position, velocity, and acceleration, thereby improving the quality and speed of the data generation at the same time. HOLD is composed of one Ornstein-Uhlenbeck process and two Hamiltonians, which reduce the mixing time by two orders of magnitude. Empirical experiments for unconditional image generation on the public data set CIFAR-10 and CelebA-HQ show that the effect is significant in both Frechet inception distance (FID) and negative log-likelihood, and achieves the state-of-the-art FID of 1.85 on CIFAR-10.

ItôWave: Itô Stochastic Differential Equation Is All You Need For Wave Generation

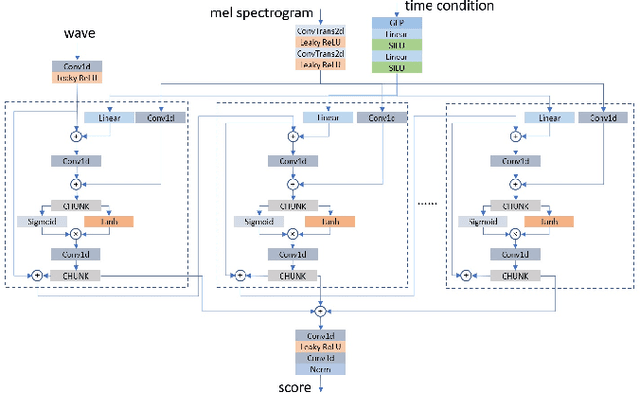
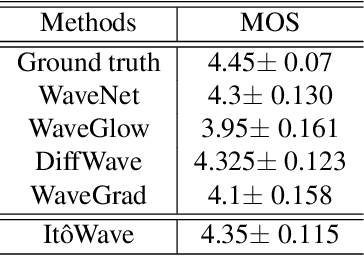
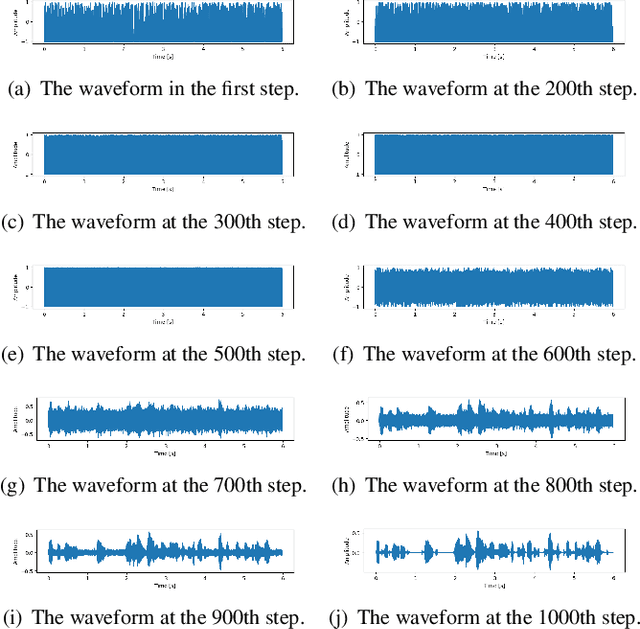
In this paper, we propose a vocoder based on a pair of forward and reverse-time linear stochastic differential equations (SDE). The solutions of this SDE pair are two stochastic processes, one of which turns the distribution of wave, that we want to generate, into a simple and tractable distribution. The other is the generation procedure that turns this tractable simple signal into the target wave. The model is called It\^oWave. It\^oWave use the Wiener process as a driver to gradually subtract the excess signal from the noise signal to generate realistic corresponding meaningful audio respectively, under the conditional inputs of original mel spectrogram. The results of the experiment show that the mean opinion scores (MOS) of It\^oWave can exceed the current state-of-the-art (SOTA) methods, and reached 4.35$\pm$0.115. The generated audio samples are available online\footnotemark[2].

Multi-modal Affect Analysis using standardized data within subjects in the Wild

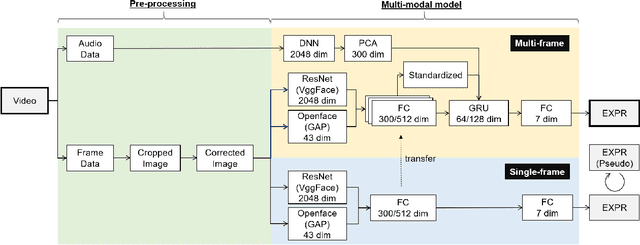
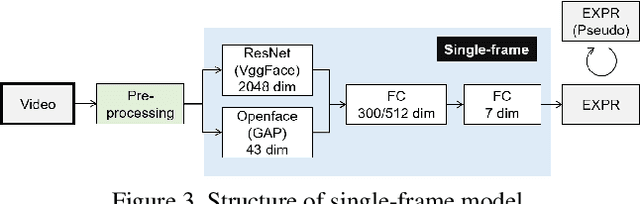
Human affective recognition is an important factor in human-computer interaction. However, the method development with in-the-wild data is not yet accurate enough for practical usage. In this paper, we introduce the affective recognition method focusing on facial expression (EXP) and valence-arousal calculation that was submitted to the Affective Behavior Analysis in-the-wild (ABAW) 2021 Contest. When annotating facial expressions from a video, we thought that it would be judged not only from the features common to all people, but also from the relative changes in the time series of individuals. Therefore, after learning the common features for each frame, we constructed a facial expression estimation model and valence-arousal model using time-series data after combining the common features and the standardized features for each video. Furthermore, the above features were learned using multi-modal data such as image features, AU, Head pose, and Gaze. In the validation set, our model achieved a facial expression score of 0.546. These verification results reveal that our proposed framework can improve estimation accuracy and robustness effectively.

It$\hat{\text{o}}$TTS and It$\hat{\text{o}}$Wave: Linear Stochastic Differential Equation Is All You Need For Audio Generation

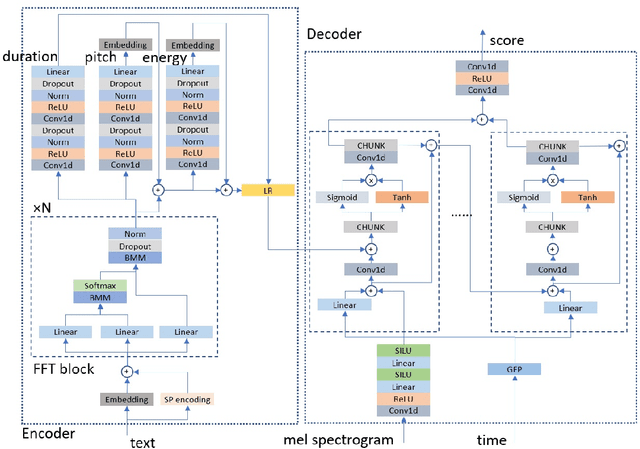
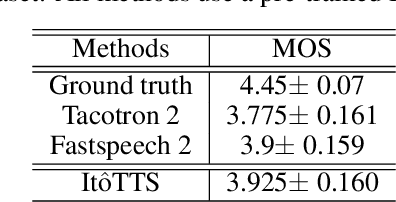
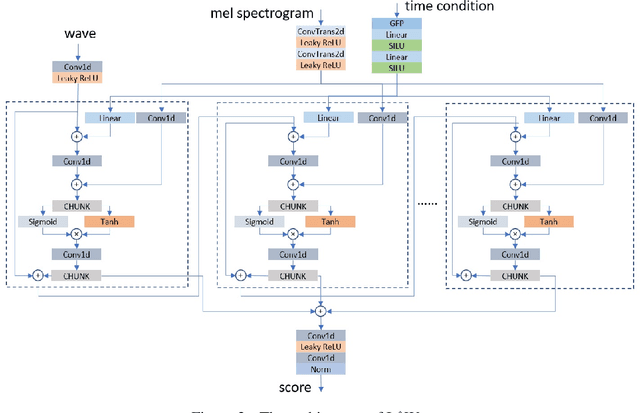
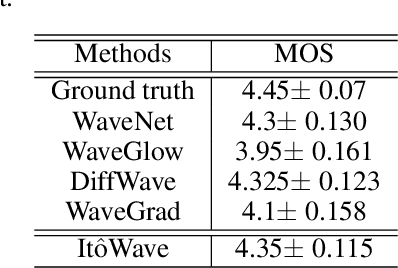
In this paper, we propose to unify the two aspects of voice synthesis, namely text-to-speech (TTS) and vocoder, into one framework based on a pair of forward and reverse-time linear stochastic differential equations (SDE). The solutions of this SDE pair are two stochastic processes, one of which turns the distribution of mel spectrogram (or wave), that we want to generate, into a simple and tractable distribution. The other is the generation procedure that turns this tractable simple signal into the target mel spectrogram (or wave). The model that generates mel spectrogram is called It$\hat{\text{o}}$TTS, and the model that generates wave is called It$\hat{\text{o}}$Wave. It$\hat{\text{o}}$TTS and It$\hat{\text{o}}$Wave use the Wiener process as a driver to gradually subtract the excess signal from the noise signal to generate realistic corresponding meaningful mel spectrogram and audio respectively, under the conditional inputs of original text or mel spectrogram. The results of the experiment show that the mean opinion scores (MOS) of It$\hat{\text{o}}$TTS and It$\hat{\text{o}}$Wave can exceed the current state-of-the-art methods, reached 3.925$\pm$0.160 and 4.35$\pm$0.115 respectively.

LoRRaL: Facial Action Unit Detection Based on Local Region Relation Learning

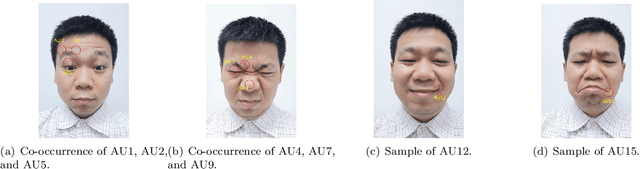
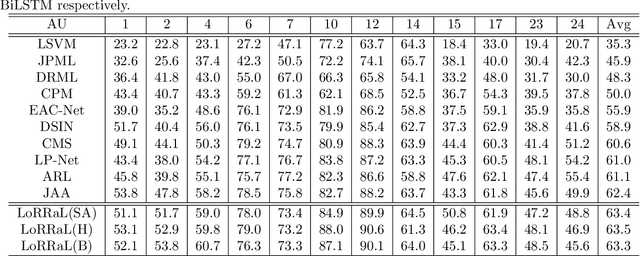
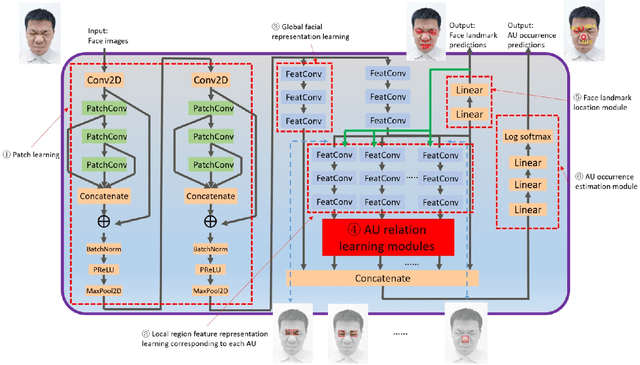
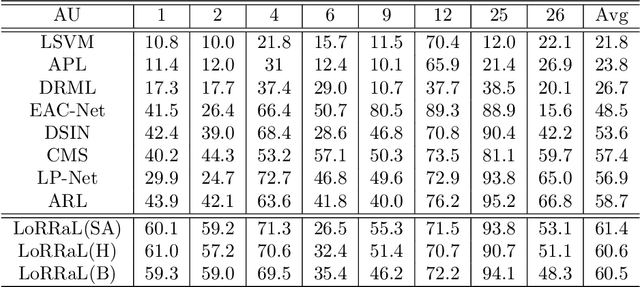
End-to-end convolution representation learning has been proved to be very effective in facial action unit (AU) detection. Considering the co-occurrence and mutual exclusion between facial AUs, in this paper, we propose convolution neural networks with Local Region Relation Learning (LoRRaL), which can combine latent relationships among AUs for an end-to-end approach to facial AU occurrence detection. LoRRaL consists of 1) use bi-directional long short-term memory (BiLSTM) to dynamically and sequentially encode local AU feature maps, 2) use self-attention mechanism to dynamically compute correspondences from local facial regions and to re-aggregate AU feature maps considering AU co-occurrences and mutual exclusions, 3) use a continuous-state modern Hopfield network to encode and map local facial features to more discriminative AU feature maps, that all these networks take the facial image as input and map it to AU occurrences. Our experiments on the challenging BP4D and DISFA Benchmarks without any external data or pre-trained models results in F1-scores of 63.5% and 61.4% respectively, which shows our proposed networks can lead to performance improvement on the AU detection task.

Learning from Adversarial Features for Few-Shot Classification

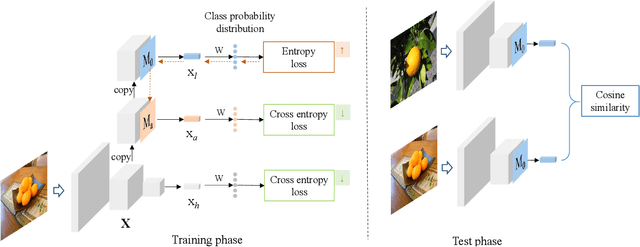
Many recent few-shot learning methods concentrate on designing novel model architectures. In this paper, we instead show that with a simple backbone convolutional network we can even surpass state-of-the-art classification accuracy. The essential part that contributes to this superior performance is an adversarial feature learning strategy that improves the generalization capability of our model. In this work, adversarial features are those features that can cause the classifier uncertain about its prediction. In order to generate adversarial features, we firstly locate adversarial regions based on the derivative of the entropy with respect to an averaging mask. Then we use the adversarial region attention to aggregate the feature maps to obtain the adversarial features. In this way, we can explore and exploit the entire spatial area of the feature maps to mine more diverse discriminative knowledge. We perform extensive model evaluations and analyses on miniImageNet and tieredImageNet datasets demonstrating the effectiveness of the proposed method.

Multi-view (Joint) Probability Linear Discrimination Analysis for Multi-view Feature Verification

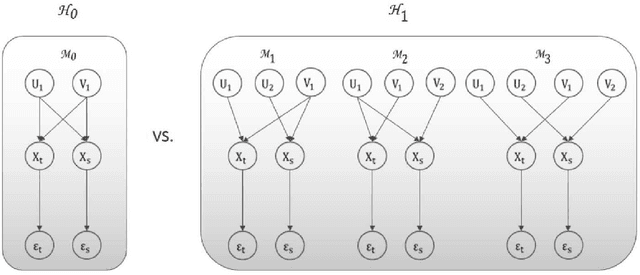
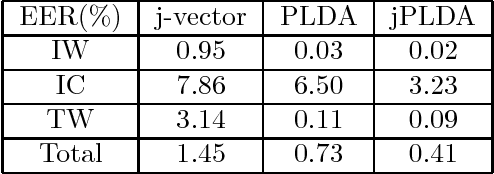
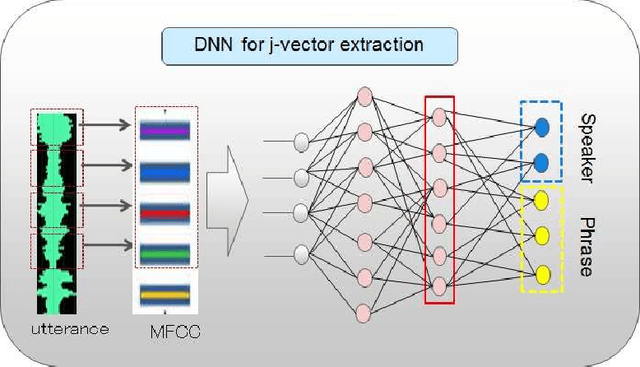
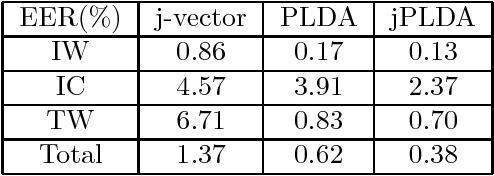
Multi-view feature has been proved to be very effective in many multimedia applications. However, the current back-end classifiers cannot make full use of such features. In this paper, we propose a method to model the multi-faceted information in the multi-view features explicitly and jointly. In our approach, the feature was modeled as a result derived by a generative multi-view (joint\footnotemark[1]) Probability Linear Discriminant Analysis (PLDA) model, which contains multiple kinds of latent variables. The usual PLDA model only considers one single label. However, in practical use, when using multi-task learned network as feature extractor, the extracted feature are always attached to several labels. This type of feature is called multi-view feature. With multi-view (joint) PLDA, we are able to explicitly build a model that can combine multiple heterogeneous information from the multi-view features. In verification step, we calculated the likelihood to describe whether the two features having consistent labels or not. This likelihood are used in the following decision-making. Experiments have been conducted on large scale verification task. On the public RSR2015 data corpus, the results showed that our approach can achieve 0.02\% EER and 0.09\% EER for impostor wrong and impostor correct cases respectively.

Online and stochastic Douglas-Rachford splitting method for large scale machine learning

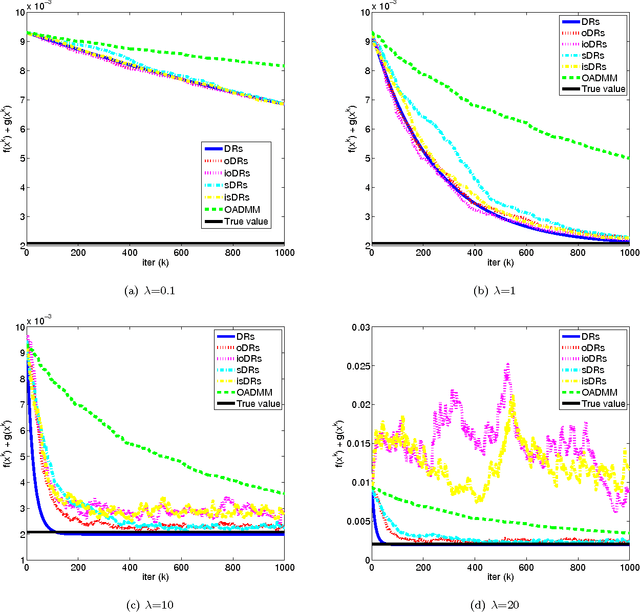
Online and stochastic learning has emerged as powerful tool in large scale optimization. In this work, we generalize the Douglas-Rachford splitting (DRs) method for minimizing composite functions to online and stochastic settings (to our best knowledge this is the first time DRs been generalized to sequential version). We first establish an $O(1/\sqrt{T})$ regret bound for batch DRs method. Then we proved that the online DRs splitting method enjoy an $O(1)$ regret bound and stochastic DRs splitting has a convergence rate of $O(1/\sqrt{T})$. The proof is simple and intuitive, and the results and technique can be served as a initiate for the research on the large scale machine learning employ the DRs method. Numerical experiments of the proposed method demonstrate the effectiveness of the online and stochastic update rule, and further confirm our regret and convergence analysis.

Empirical study of PROXTONE and PROXTONE$^+$ for Fast Learning of Large Scale Sparse Models

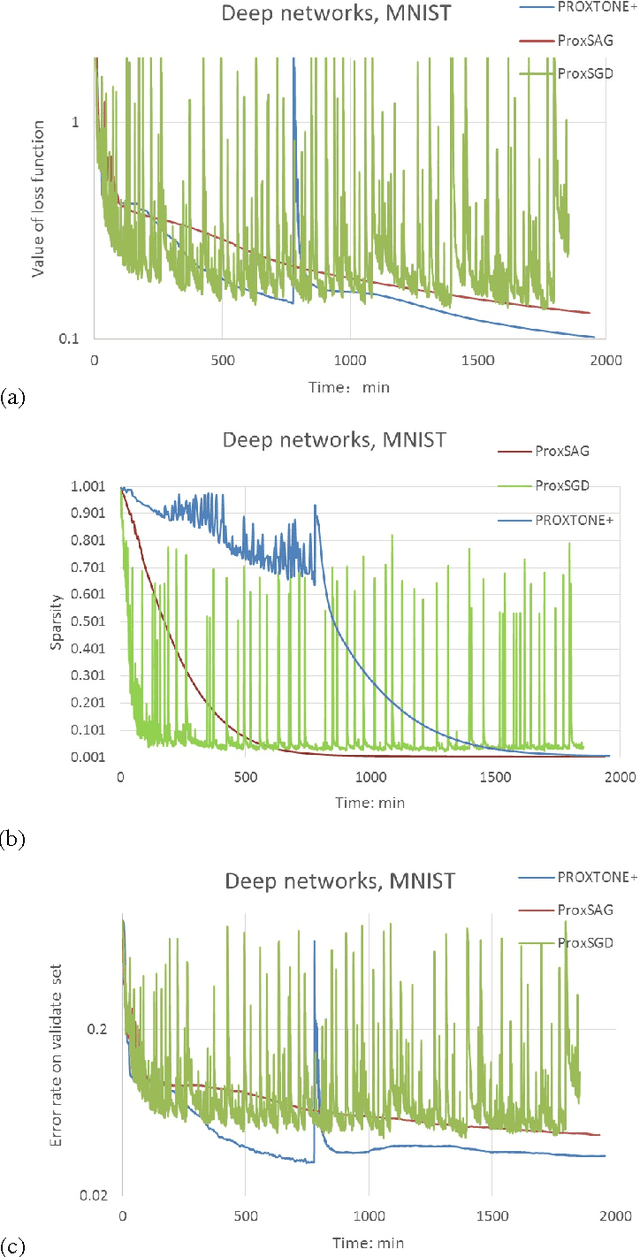
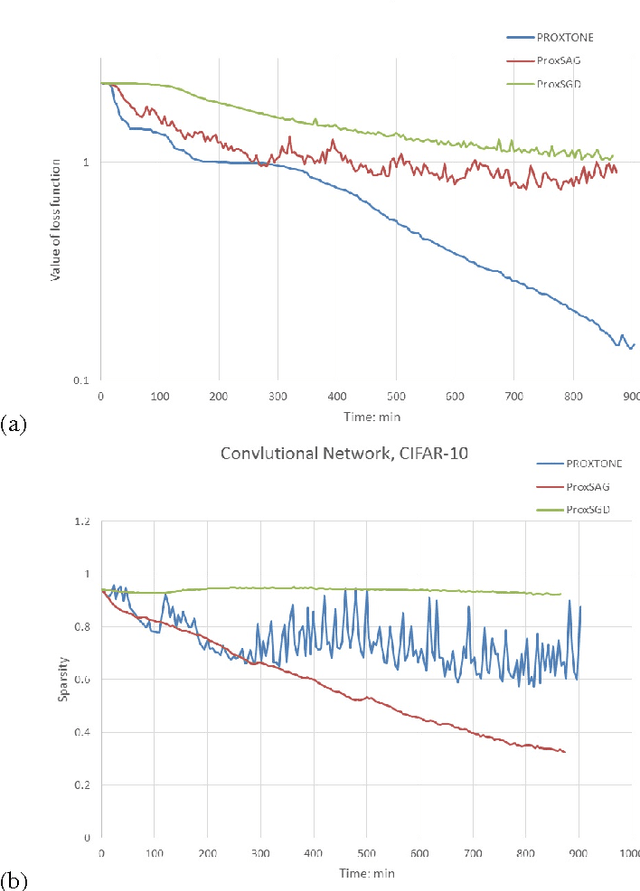
PROXTONE is a novel and fast method for optimization of large scale non-smooth convex problem \cite{shi2015large}. In this work, we try to use PROXTONE method in solving large scale \emph{non-smooth non-convex} problems, for example training of sparse deep neural network (sparse DNN) or sparse convolutional neural network (sparse CNN) for embedded or mobile device. PROXTONE converges much faster than first order methods, while first order method is easy in deriving and controlling the sparseness of the solutions. Thus in some applications, in order to train sparse models fast, we propose to combine the merits of both methods, that is we use PROXTONE in the first several epochs to reach the neighborhood of an optimal solution, and then use the first order method to explore the possibility of sparsity in the following training. We call such method PROXTONE plus (PROXTONE$^+$). Both PROXTONE and PROXTONE$^+$ are tested in our experiments, and which demonstrate both methods improved convergence speed twice as fast at least on diverse sparse model learning problems, and at the same time reduce the size to 0.5\% for DNN models. The source of all the algorithms is available upon request.

Guarantees of Augmented Trace Norm Models in Tensor Recovery

This paper studies the recovery guarantees of the models of minimizing $\|\mathcal{X}\|_*+\frac{1}{2\alpha}\|\mathcal{X}\|_F^2$ where $\mathcal{X}$ is a tensor and $\|\mathcal{X}\|_*$ and $\|\mathcal{X}\|_F$ are the trace and Frobenius norm of respectively. We show that they can efficiently recover low-rank tensors. In particular, they enjoy exact guarantees similar to those known for minimizing $\|\mathcal{X}\|_*$ under the conditions on the sensing operator such as its null-space property, restricted isometry property, or spherical section property. To recover a low-rank tensor $\mathcal{X}^0$, minimizing $\|\mathcal{X}\|_*+\frac{1}{2\alpha}\|\mathcal{X}\|_F^2$ returns the same solution as minimizing $\|\mathcal{X}\|_*$ almost whenever $\alpha\geq10\mathop {\max}\limits_{i}\|X^0_{(i)}\|_2$.