Zhihan Xiong
LoRe: Personalizing LLMs via Low-Rank Reward Modeling
Apr 20, 2025



Abstract:Personalizing large language models (LLMs) to accommodate diverse user preferences is essential for enhancing alignment and user satisfaction. Traditional reinforcement learning from human feedback (RLHF) approaches often rely on monolithic value representations, limiting their ability to adapt to individual preferences. We introduce a novel framework that leverages low-rank preference modeling to efficiently learn and generalize user-specific reward functions. By representing reward functions in a low-dimensional subspace and modeling individual preferences as weighted combinations of shared basis functions, our approach avoids rigid user categorization while enabling scalability and few-shot adaptation. We validate our method on multiple preference datasets, demonstrating superior generalization to unseen users and improved accuracy in preference prediction tasks.
Hybrid Preference Optimization for Alignment: Provably Faster Convergence Rates by Combining Offline Preferences with Online Exploration
Dec 13, 2024Abstract:Reinforcement Learning from Human Feedback (RLHF) is currently the leading approach for aligning large language models with human preferences. Typically, these models rely on extensive offline preference datasets for training. However, offline algorithms impose strict concentrability requirements, which are often difficult to satisfy. On the other hand, while online algorithms can avoid the concentrability issue, pure online exploration could be expensive due to the active preference query cost and real-time implementation overhead. In this paper, we propose a novel approach: Hybrid Preference Optimization (HPO) which combines online exploration with existing offline preferences by relaxing the stringent concentrability conditions for offline exploration, as well as significantly improving the sample efficiency for its online counterpart. We give the first provably optimal theoretical bound for Hybrid RLHF with preference feedback, providing sample complexity bounds for policy optimization with matching lower bounds. Our results yield improved sample efficiency of hybrid RLHF over pure offline and online exploration.
Language Model Preference Evaluation with Multiple Weak Evaluators
Oct 14, 2024



Abstract:Despite the remarkable success of Large Language Models (LLMs), evaluating their outputs' quality regarding preference remains a critical challenge. Existing works usually leverage a powerful LLM (e.g., GPT4) as the judge for comparing LLMs' output pairwisely, yet such model-based evaluator is vulnerable to conflicting preference, i.e., output A is better than B, B than C, but C than A, causing contradictory evaluation results. To improve model-based preference evaluation, we introduce GED (Preference Graph Ensemble and Denoise), a novel approach that leverages multiple model-based evaluators to construct preference graphs, and then ensemble and denoise these graphs for better, non-contradictory evaluation results. In particular, our method consists of two primary stages: aggregating evaluations into a unified graph and applying a denoising process to eliminate cyclic inconsistencies, ensuring a directed acyclic graph (DAG) structure. We provide theoretical guarantees for our framework, demonstrating its efficacy in recovering the ground truth preference structure. Extensive experiments across ten benchmark datasets show that GED outperforms baseline methods in model ranking, response selection, and model alignment tasks. Notably, GED combines weaker evaluators like Llama3-8B, Mistral-7B, and Qwen2-7B to surpass the performance of stronger evaluators like Qwen2-72B, highlighting its ability to enhance evaluation reliability and improve model performance.
Dual Approximation Policy Optimization
Oct 02, 2024



Abstract:We propose Dual Approximation Policy Optimization (DAPO), a framework that incorporates general function approximation into policy mirror descent methods. In contrast to the popular approach of using the $L_2$-norm to measure function approximation errors, DAPO uses the dual Bregman divergence induced by the mirror map for policy projection. This duality framework has both theoretical and practical implications: not only does it achieve fast linear convergence with general function approximation, but it also includes several well-known practical methods as special cases, immediately providing strong convergence guarantees.
A/B Testing and Best-arm Identification for Linear Bandits with Robustness to Non-stationarity
Jul 27, 2023Abstract:We investigate the fixed-budget best-arm identification (BAI) problem for linear bandits in a potentially non-stationary environment. Given a finite arm set $\mathcal{X}\subset\mathbb{R}^d$, a fixed budget $T$, and an unpredictable sequence of parameters $\left\lbrace\theta_t\right\rbrace_{t=1}^{T}$, an algorithm will aim to correctly identify the best arm $x^* := \arg\max_{x\in\mathcal{X}}x^\top\sum_{t=1}^{T}\theta_t$ with probability as high as possible. Prior work has addressed the stationary setting where $\theta_t = \theta_1$ for all $t$ and demonstrated that the error probability decreases as $\exp(-T /\rho^*)$ for a problem-dependent constant $\rho^*$. But in many real-world $A/B/n$ multivariate testing scenarios that motivate our work, the environment is non-stationary and an algorithm expecting a stationary setting can easily fail. For robust identification, it is well-known that if arms are chosen randomly and non-adaptively from a G-optimal design over $\mathcal{X}$ at each time then the error probability decreases as $\exp(-T\Delta^2_{(1)}/d)$, where $\Delta_{(1)} = \min_{x \neq x^*} (x^* - x)^\top \frac{1}{T}\sum_{t=1}^T \theta_t$. As there exist environments where $\Delta_{(1)}^2/ d \ll 1/ \rho^*$, we are motivated to propose a novel algorithm $\mathsf{P1}$-$\mathsf{RAGE}$ that aims to obtain the best of both worlds: robustness to non-stationarity and fast rates of identification in benign settings. We characterize the error probability of $\mathsf{P1}$-$\mathsf{RAGE}$ and demonstrate empirically that the algorithm indeed never performs worse than G-optimal design but compares favorably to the best algorithms in the stationary setting.
A Black-box Approach for Non-stationary Multi-agent Reinforcement Learning
Jun 12, 2023
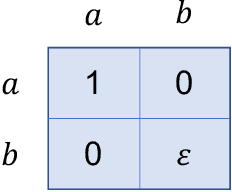

Abstract:We investigate learning the equilibria in non-stationary multi-agent systems and address the challenges that differentiate multi-agent learning from single-agent learning. Specifically, we focus on games with bandit feedback, where testing an equilibrium can result in substantial regret even when the gap to be tested is small, and the existence of multiple optimal solutions (equilibria) in stationary games poses extra challenges. To overcome these obstacles, we propose a versatile black-box approach applicable to a broad spectrum of problems, such as general-sum games, potential games, and Markov games, when equipped with appropriate learning and testing oracles for stationary environments. Our algorithms can achieve $\widetilde{O}\left(\Delta^{1/4}T^{3/4}\right)$ regret when the degree of nonstationarity, as measured by total variation $\Delta$, is known, and $\widetilde{O}\left(\Delta^{1/5}T^{4/5}\right)$ regret when $\Delta$ is unknown, where $T$ is the number of rounds. Meanwhile, our algorithm inherits the favorable dependence on number of agents from the oracles. As a side contribution that may be independent of interest, we show how to test for various types of equilibria by a black-box reduction to single-agent learning, which includes Nash equilibria, correlated equilibria, and coarse correlated equilibria.
Offline congestion games: How feedback type affects data coverage requirement
Oct 24, 2022Abstract:This paper investigates when one can efficiently recover an approximate Nash Equilibrium (NE) in offline congestion games.The existing dataset coverage assumption in offline general-sum games inevitably incurs a dependency on the number of actions, which can be exponentially large in congestion games. We consider three different types of feedback with decreasing revealed information. Starting from the facility-level (a.k.a., semi-bandit) feedback, we propose a novel one-unit deviation coverage condition and give a pessimism-type algorithm that can recover an approximate NE. For the agent-level (a.k.a., bandit) feedback setting, interestingly, we show the one-unit deviation coverage condition is not sufficient. On the other hand, we convert the game to multi-agent linear bandits and show that with a generalized data coverage assumption in offline linear bandits, we can efficiently recover the approximate NE. Lastly, we consider a novel type of feedback, the game-level feedback where only the total reward from all agents is revealed. Again, we show the coverage assumption for the agent-level feedback setting is insufficient in the game-level feedback setting, and with a stronger version of the data coverage assumption for linear bandits, we can recover an approximate NE. Together, our results constitute the first study of offline congestion games and imply formal separations between different types of feedback.
Learning in Congestion Games with Bandit Feedback
Jun 04, 2022
Abstract:Learning Nash equilibria is a central problem in multi-agent systems. In this paper, we investigate congestion games, a class of games with benign theoretical structure and broad real-world applications. We first propose a centralized algorithm based on the optimism in the face of uncertainty principle for congestion games with (semi-)bandit feedback, and obtain finite-sample guarantees. Then we propose a decentralized algorithm via a novel combination of the Frank-Wolfe method and G-optimal design. By exploiting the structure of the congestion game, we show the sample complexity of both algorithms depends only polynomially on the number of players and the number of facilities, but not the size of the action set, which can be exponentially large in terms of the number of facilities. We further define a new problem class, Markov congestion games, which allows us to model the non-stationarity in congestion games. We propose a centralized algorithm for Markov congestion games, whose sample complexity again has only polynomial dependence on all relevant problem parameters, but not the size of the action set.
Selective Sampling for Online Best-arm Identification
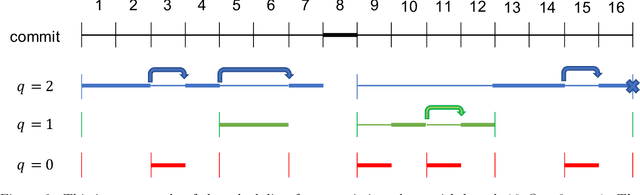
Nov 02, 2021
Abstract:This work considers the problem of selective-sampling for best-arm identification. Given a set of potential options $\mathcal{Z}\subset\mathbb{R}^d$, a learner aims to compute with probability greater than $1-\delta$, $\arg\max_{z\in \mathcal{Z}} z^{\top}\theta_{\ast}$ where $\theta_{\ast}$ is unknown. At each time step, a potential measurement $x_t\in \mathcal{X}\subset\mathbb{R}^d$ is drawn IID and the learner can either choose to take the measurement, in which case they observe a noisy measurement of $x^{\top}\theta_{\ast}$, or to abstain from taking the measurement and wait for a potentially more informative point to arrive in the stream. Hence the learner faces a fundamental trade-off between the number of labeled samples they take and when they have collected enough evidence to declare the best arm and stop sampling. The main results of this work precisely characterize this trade-off between labeled samples and stopping time and provide an algorithm that nearly-optimally achieves the minimal label complexity given a desired stopping time. In addition, we show that the optimal decision rule has a simple geometric form based on deciding whether a point is in an ellipse or not. Finally, our framework is general enough to capture binary classification improving upon previous works.
Randomized Exploration is Near-Optimal for Tabular MDP
Feb 19, 2021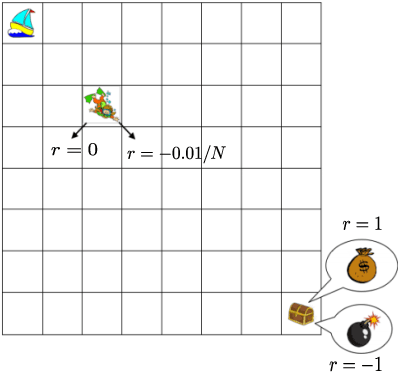
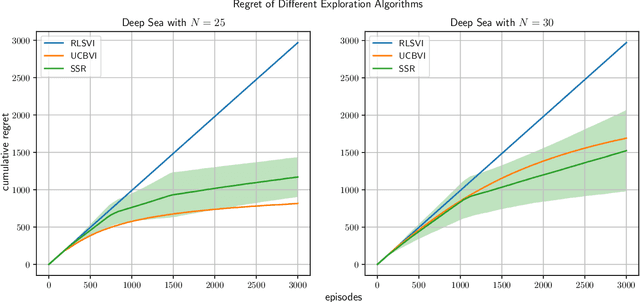
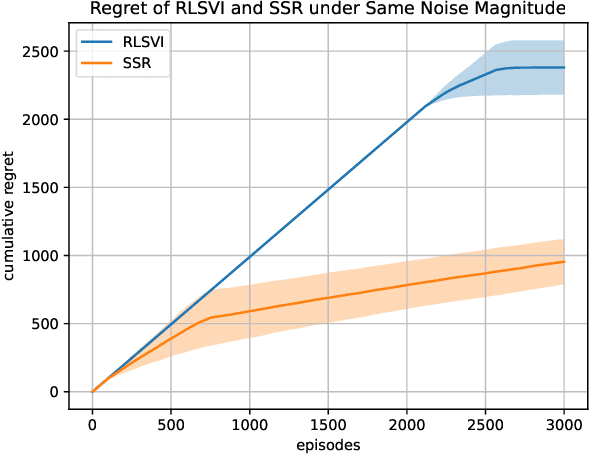
Abstract:We study exploration using randomized value functions in Thompson Sampling (TS)-like algorithms in reinforcement learning. This type of algorithms enjoys appealing empirical performance. We show that when we use 1) a single random seed in each episode, and 2) a Bernstein-type magnitude of noise, we obtain a worst-case $\widetilde{O}\left(H\sqrt{SAT}\right)$ regret bound for episodic time-inhomogeneous Markov Decision Process where $S$ is the size of state space, $A$ is the size of action space, $H$ is the planning horizon and $T$ is the number of interactions. This bound polynomially improves all existing bounds for TS-like algorithms based on randomized value functions, and for the first time, matches the $\Omega\left(H\sqrt{SAT}\right)$ lower bound up to logarithmic factors. Our result highlights that randomized exploration can be near-optimal, which was previously only achieved by optimistic algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge