Improving Monte Carlo Tree Search for Symbolic Regression

Symbolic regression aims to discover concise, interpretable mathematical expressions that satisfy desired objectives, such as fitting data, posing a highly combinatorial optimization problem. While genetic programming has been the dominant approach, recent efforts have explored reinforcement learning methods for improving search efficiency. Monte Carlo Tree Search (MCTS), with its ability to balance exploration and exploitation through guided search, has emerged as a promising technique for symbolic expression discovery. However, its traditional bandit strategies and sequential symbol construction often limit performance. In this work, we propose an improved MCTS framework for symbolic regression that addresses these limitations through two key innovations: (1) an extreme bandit allocation strategy tailored for identifying globally optimal expressions, with finite-time performance guarantees under polynomial reward decay assumptions; and (2) evolution-inspired state-jumping actions such as mutation and crossover, which enable non-local transitions to promising regions of the search space. These state-jumping actions also reshape the reward landscape during the search process, improving both robustness and efficiency. We conduct a thorough numerical study to the impact of these improvements and benchmark our approach against existing symbolic regression methods on a variety of datasets, including both ground-truth and black-box datasets. Our approach achieves competitive performance with state-of-the-art libraries in terms of recovery rate, attains favorable positions on the Pareto frontier of accuracy versus model complexity. Code is available at https://github.com/PKU-CMEGroup/MCTS-4-SR.

BigMac: A Communication-Efficient Mixture-of-Experts Model Structure for Fast Training and Inference

The Mixture-of-Experts (MoE) structure scales the Transformer-based large language models (LLMs) and improves their performance with only the sub-linear increase in computation resources. Recently, a fine-grained DeepSeekMoE structure is proposed, which can further improve the computing efficiency of MoE without performance degradation. However, the All-to-All communication introduced by MoE has become a bottleneck, especially for the fine-grained structure, which typically involves and activates more experts, hence contributing to heavier communication overhead. In this paper, we propose a novel MoE structure named BigMac, which is also fine-grained but with high communication efficiency. The innovation of BigMac is mainly due to that we abandon the \textbf{c}ommunicate-\textbf{d}escend-\textbf{a}scend-\textbf{c}ommunicate (CDAC) manner used by fine-grained MoE, which leads to the All-to-All communication always taking place at the highest dimension. Instead, BigMac designs an efficient \textbf{d}escend-\textbf{c}ommunicate-\textbf{c}ommunicate-\textbf{a}scend (DCCA) manner. Specifically, we add a descending and ascending projection at the entrance and exit of the expert, respectively, which enables the communication to perform at a very low dimension. Furthermore, to adapt to DCCA, we re-design the structure of small experts, ensuring that the expert in BigMac has enough complexity to address tokens. Experimental results show that BigMac achieves comparable or even better model quality than fine-grained MoEs with the same number of experts and a similar number of total parameters. Equally importantly, BigMac reduces the end-to-end latency by up to 3.09$\times$ for training and increases the throughput by up to 3.11$\times$ for inference on state-of-the-art AI computing frameworks including Megatron, Tutel, and DeepSpeed-Inference.

Harmonic Retrieval with $L_1$-Tucker Tensor Decomposition

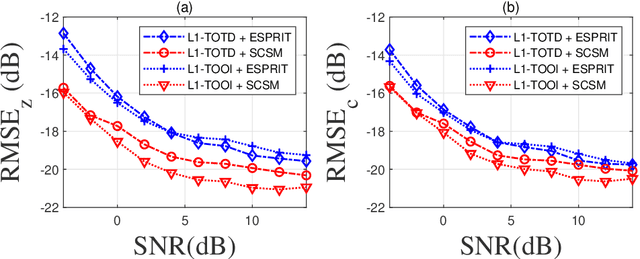
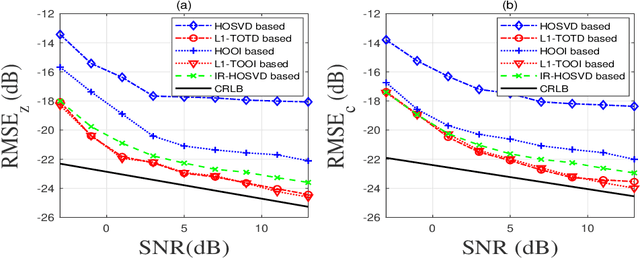
Harmonic retrieval (HR) has a wide range of applications in the scenes where signals are modelled as a summation of sinusoids. Past works have developed a number of approaches to recover the original signals. Most of them rely on classical singular value decomposition, which are vulnerable to unexpected outliers. In this paper, we present new decomposition algorithms of third-order complex-valued tensors with $L_1$-principle component analysis ($L_1$-PCA) of complex data and apply them to a novel random access HR model in presence of outliers. We also develop a novel subcarrier recovery method for the proposed model. Simulations are designed to compare our proposed method with some existing tensor-based algorithms for HR. The results demonstrate the outlier-insensitivity of the proposed method.