Hardware-Adaptive and Superlinear-Capacity Memristor-based Associative Memory

Brain-inspired computing aims to mimic cognitive functions like associative memory, the ability to recall complete patterns from partial cues. Memristor technology offers promising hardware for such neuromorphic systems due to its potential for efficient in-memory analog computing. Hopfield Neural Networks (HNNs) are a classic model for associative memory, but implementations on conventional hardware suffer from efficiency bottlenecks, while prior memristor-based HNNs faced challenges with vulnerability to hardware defects due to offline training, limited storage capacity, and difficulty processing analog patterns. Here we introduce and experimentally demonstrate on integrated memristor hardware a new hardware-adaptive learning algorithm for associative memories that significantly improves defect tolerance and capacity, and naturally extends to scalable multilayer architectures capable of handling both binary and continuous patterns. Our approach achieves 3x effective capacity under 50% device faults compared to state-of-the-art methods. Furthermore, its extension to multilayer architectures enables superlinear capacity scaling (\(\propto N^{1.49}\ for binary patterns) and effective recalling of continuous patterns (\propto N^{1.74}\ scaling), as compared to linear capacity scaling for previous HNNs. It also provides flexibility to adjust capacity by tuning hidden neurons for the same-sized patterns. By leveraging the massive parallelism of the hardware enabled by synchronous updates, it reduces energy by 8.8x and latency by 99.7% for 64-dimensional patterns over asynchronous schemes, with greater improvements at scale. This promises the development of more reliable memristor-based associative memory systems and enables new applications research due to the significantly improved capacity, efficiency, and flexibility.

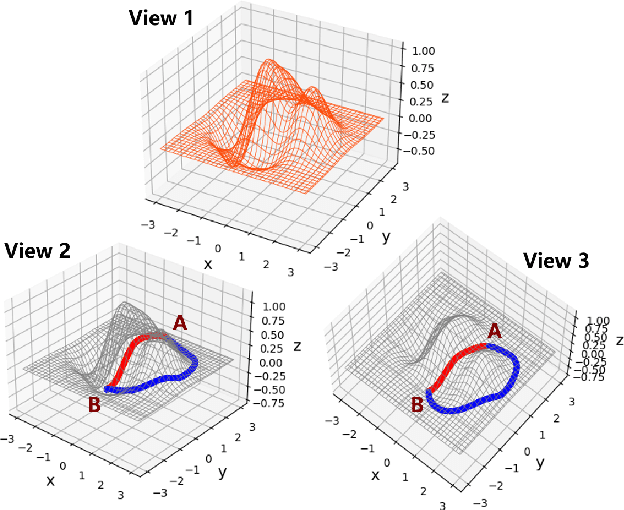
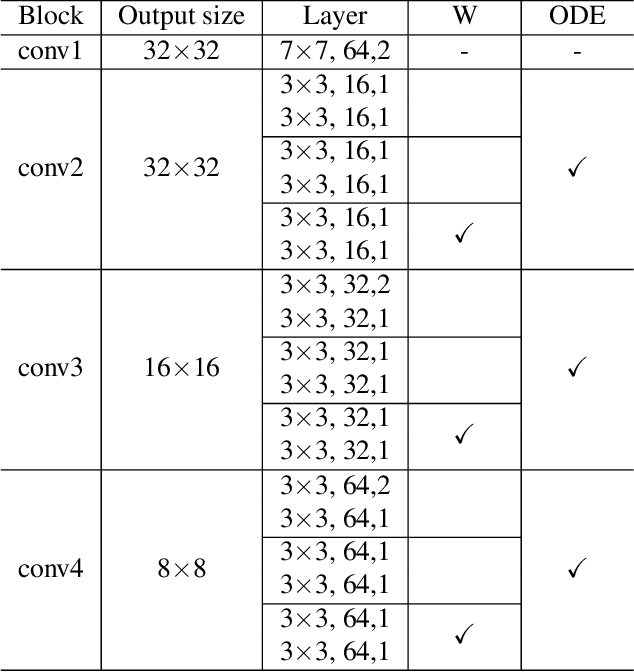
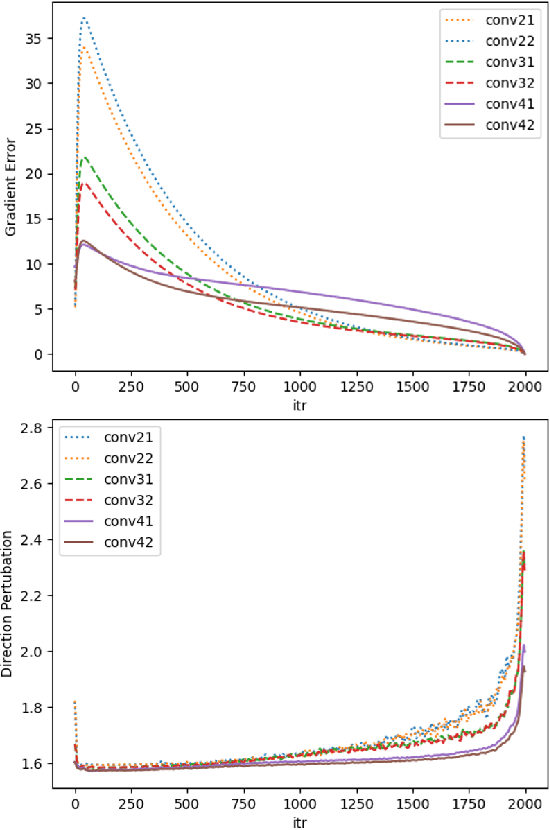
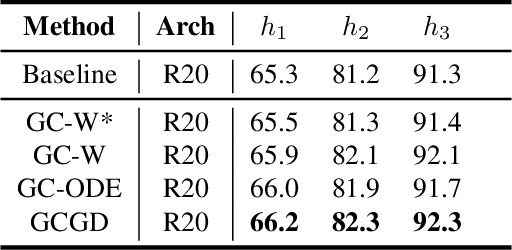
Gradient Correction beyond Gradient Descent

The great success neural networks have achieved is inseparable from the application of gradient-descent (GD) algorithms. Based on GD, many variant algorithms have emerged to improve the GD optimization process. The gradient for back-propagation is apparently the most crucial aspect for the training of a neural network. The quality of the calculated gradient can be affected by multiple aspects, e.g., noisy data, calculation error, algorithm limitation, and so on. To reveal gradient information beyond gradient descent, we introduce a framework (\textbf{GCGD}) to perform gradient correction. GCGD consists of two plug-in modules: 1) inspired by the idea of gradient prediction, we propose a \textbf{GC-W} module for weight gradient correction; 2) based on Neural ODE, we propose a \textbf{GC-ODE} module for hidden states gradient correction. Experiment results show that our gradient correction framework can effectively improve the gradient quality to reduce training epochs by $\sim$ 20\% and also improve the network performance.

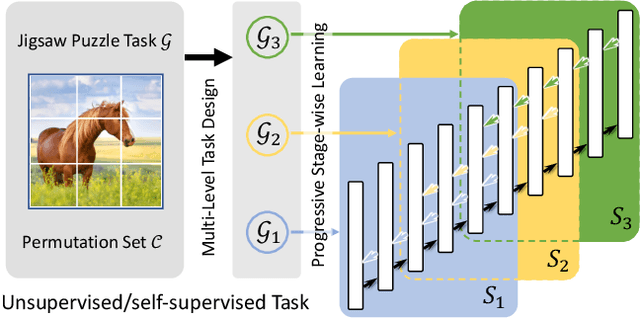
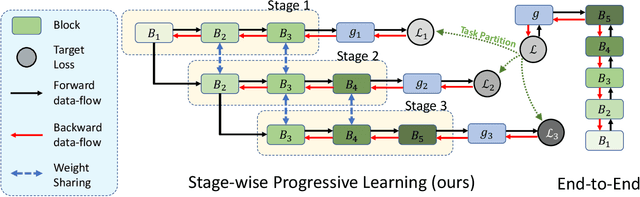
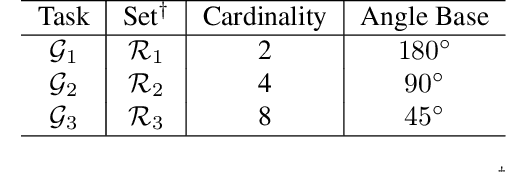
Progressive Stage-wise Learning for Unsupervised Feature Representation Enhancement

Unsupervised learning methods have recently shown their competitiveness against supervised training. Typically, these methods use a single objective to train the entire network. But one distinct advantage of unsupervised over supervised learning is that the former possesses more variety and freedom in designing the objective. In this work, we explore new dimensions of unsupervised learning by proposing the Progressive Stage-wise Learning (PSL) framework. For a given unsupervised task, we design multilevel tasks and define different learning stages for the deep network. Early learning stages are forced to focus on lowlevel tasks while late stages are guided to extract deeper information through harder tasks. We discover that by progressive stage-wise learning, unsupervised feature representation can be effectively enhanced. Our extensive experiments show that PSL consistently improves results for the leading unsupervised learning methods.

Performance Guaranteed Network Acceleration via High-Order Residual Quantization

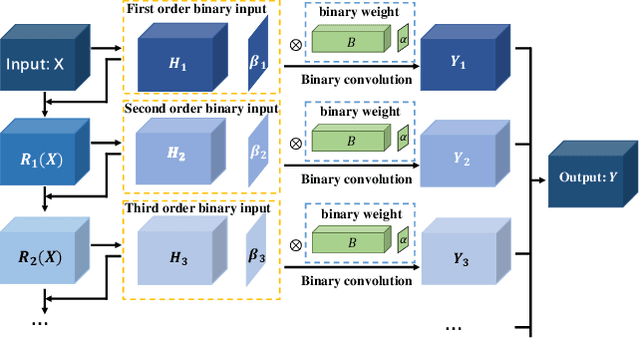
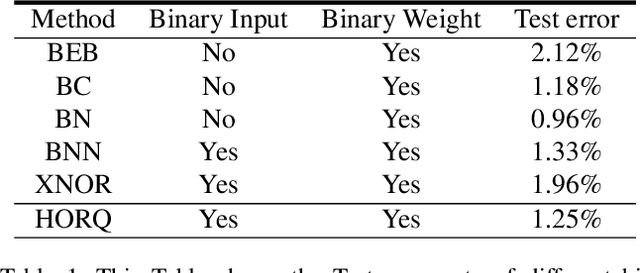
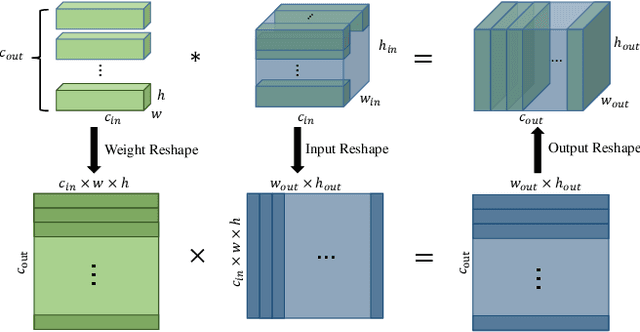
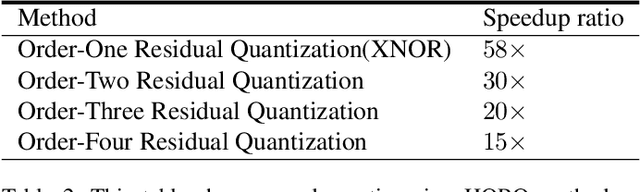
Input binarization has shown to be an effective way for network acceleration. However, previous binarization scheme could be regarded as simple pixel-wise thresholding operations (i.e., order-one approximation) and suffers a big accuracy loss. In this paper, we propose a highorder binarization scheme, which achieves more accurate approximation while still possesses the advantage of binary operation. In particular, the proposed scheme recursively performs residual quantization and yields a series of binary input images with decreasing magnitude scales. Accordingly, we propose high-order binary filtering and gradient propagation operations for both forward and backward computations. Theoretical analysis shows approximation error guarantee property of proposed method. Extensive experimental results demonstrate that the proposed scheme yields great recognition accuracy while being accelerated.