An Investigation of Potential Function Designs for Neural CRF

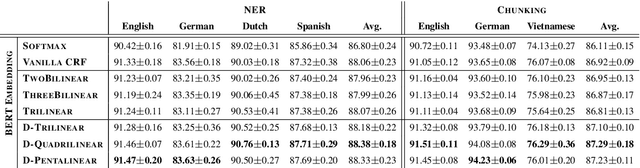
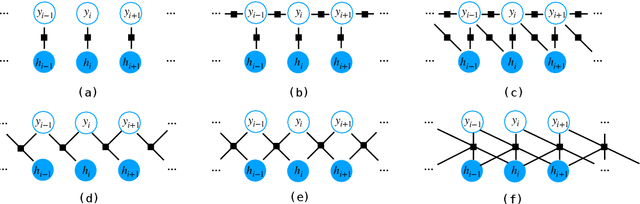
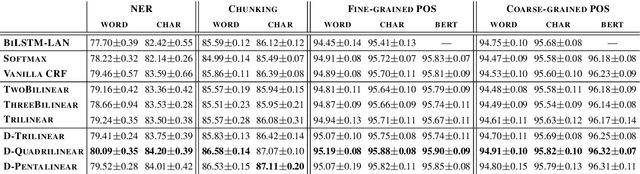
The neural linear-chain CRF model is one of the most widely-used approach to sequence labeling. In this paper, we investigate a series of increasingly expressive potential functions for neural CRF models, which not only integrate the emission and transition functions, but also explicitly take the representations of the contextual words as input. Our extensive experiments show that the decomposed quadrilinear potential function based on the vector representations of two neighboring labels and two neighboring words consistently achieves the best performance.

Neural Latent Dependency Model for Sequence Labeling

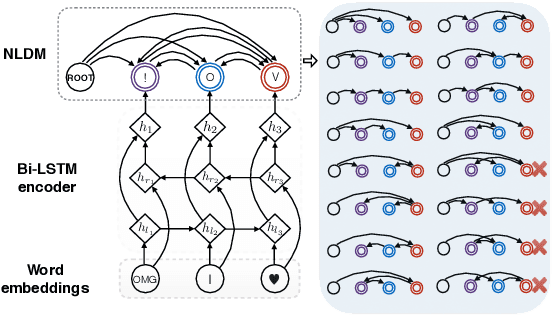
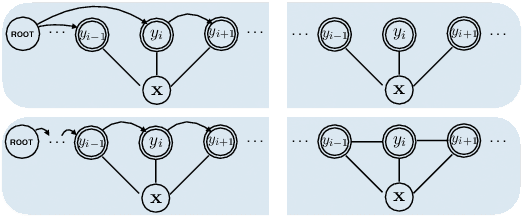
Sequence labeling is a fundamental problem in machine learning, natural language processing and many other fields. A classic approach to sequence labeling is linear chain conditional random fields (CRFs). When combined with neural network encoders, they achieve very good performance in many sequence labeling tasks. One limitation of linear chain CRFs is their inability to model long-range dependencies between labels. High order CRFs extend linear chain CRFs by modeling dependencies no longer than their order, but the computational complexity grows exponentially in the order. In this paper, we propose the Neural Latent Dependency Model (NLDM) that models dependencies of arbitrary length between labels with a latent tree structure. We develop an end-to-end training algorithm and a polynomial-time inference algorithm of our model. We evaluate our model on both synthetic and real datasets and show that our model outperforms strong baselines.