Separation Results between Fixed-Kernel and Feature-Learning Probability Metrics

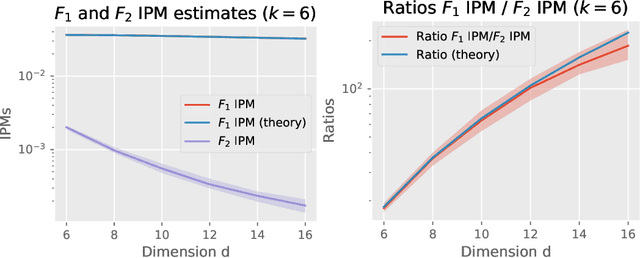
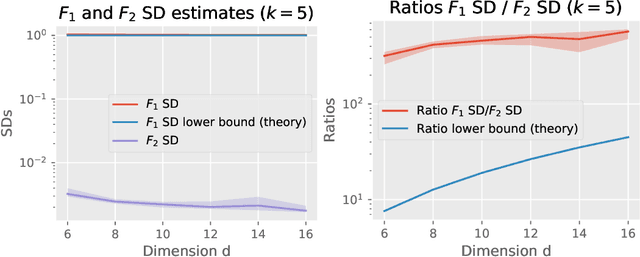
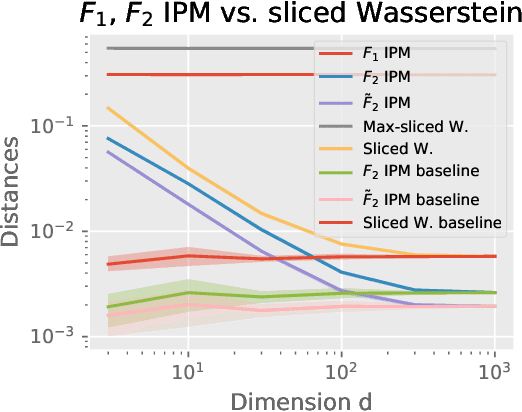
Several works in implicit and explicit generative modeling empirically observed that feature-learning discriminators outperform fixed-kernel discriminators in terms of the sample quality of the models. We provide separation results between probability metrics with fixed-kernel and feature-learning discriminators using the function classes $\mathcal{F}_2$ and $\mathcal{F}_1$ respectively, which were developed to study overparametrized two-layer neural networks. In particular, we construct pairs of distributions over hyper-spheres that can not be discriminated by fixed kernel $(\mathcal{F}_2)$ integral probability metric (IPM) and Stein discrepancy (SD) in high dimensions, but that can be discriminated by their feature learning ($\mathcal{F}_1$) counterparts. To further study the separation we provide links between the $\mathcal{F}_1$ and $\mathcal{F}_2$ IPMs with sliced Wasserstein distances. Our work suggests that fixed-kernel discriminators perform worse than their feature learning counterparts because their corresponding metrics are weaker.

Do Large Scale Molecular Language Representations Capture Important Structural Information?

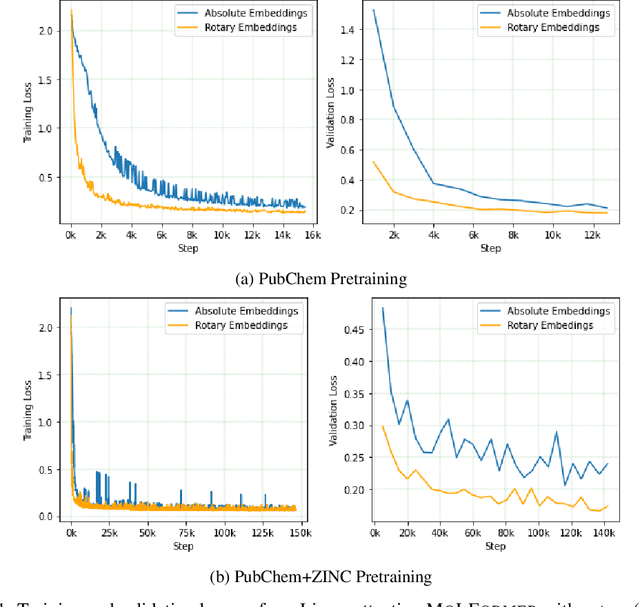
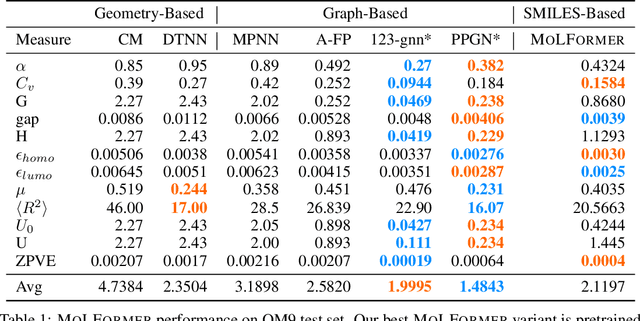
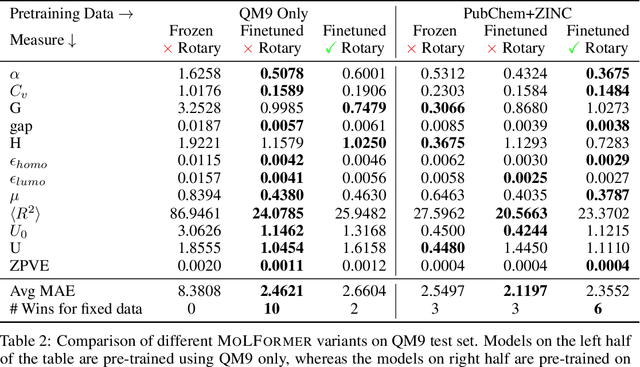
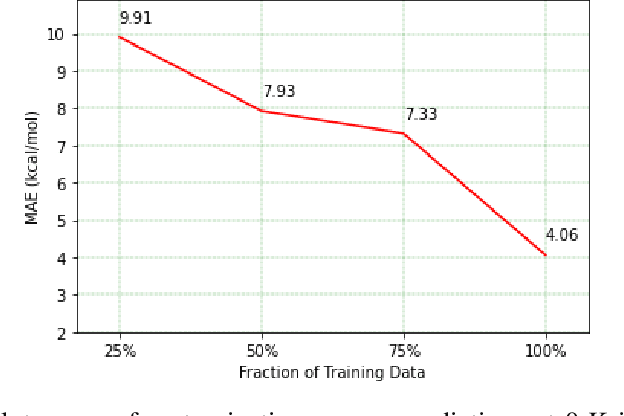
Predicting chemical properties from the structure of a molecule is of great importance in many applications including drug discovery and material design. Machine learning based molecular property prediction holds the promise of enabling accurate predictions at much less complexity, when compared to, for example Density Functional Theory (DFT) calculations. Features extracted from molecular graphs, using graph neural nets in a supervised manner, have emerged as strong baselines for such tasks. However, the vast chemical space together with the limited availability of labels makes supervised learning challenging, calling for learning a general-purpose molecular representation. Recently, pre-trained transformer-based language models (PTLMs) on large unlabeled corpus have produced state-of-the-art results in many downstream natural language processing tasks. Inspired by this development, here we present molecular embeddings obtained by training an efficient transformer encoder model, referred to as MoLFormer. This model was employed with a linear attention mechanism and highly paralleized training on 1D SMILES sequences of 1.1 billion unlabeled molecules from the PubChem and ZINC datasets. Experiments show that the learned molecular representation performs competitively, when compared to existing graph-based and fingerprint-based supervised learning baselines, on the challenging tasks of predicting properties of QM8 and QM9 molecules. Further task-specific fine-tuning of the MoLFormerr representation improves performance on several of those property prediction benchmarks. These results provide encouraging evidence that large-scale molecular language models can capture sufficient structural information to be able to accurately predict quantum chemical properties and beyond.

Optimizing Functionals on the Space of Probabilities with Input Convex Neural Networks

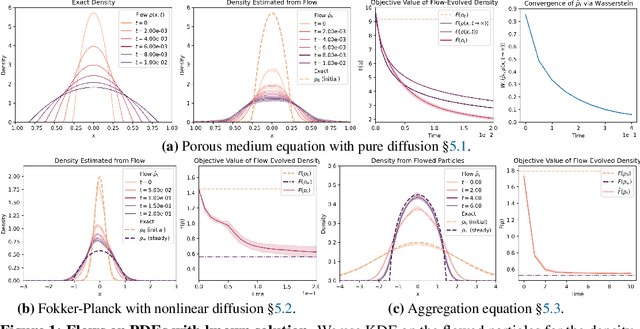
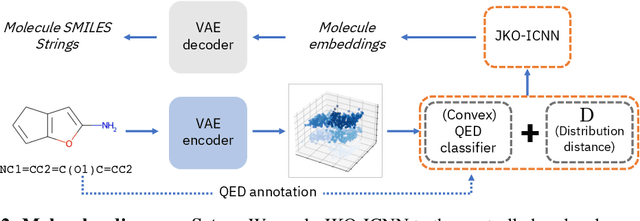
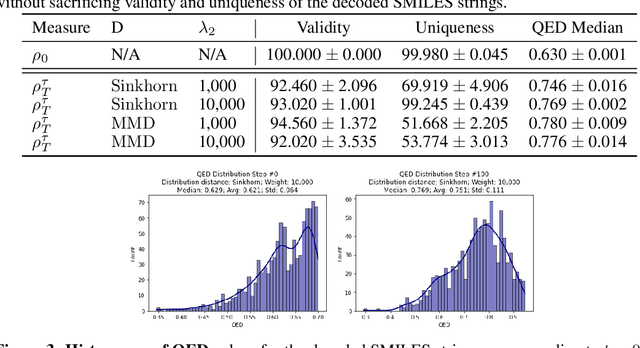
Gradient flows are a powerful tool for optimizing functionals in general metric spaces, including the space of probabilities endowed with the Wasserstein metric. A typical approach to solving this optimization problem relies on its connection to the dynamic formulation of optimal transport and the celebrated Jordan-Kinderlehrer-Otto (JKO) scheme. However, this formulation involves optimization over convex functions, which is challenging, especially in high dimensions. In this work, we propose an approach that relies on the recently introduced input-convex neural networks (ICNN) to parameterize the space of convex functions in order to approximate the JKO scheme, as well as in designing functionals over measures that enjoy convergence guarantees. We derive a computationally efficient implementation of this JKO-ICNN framework and use various experiments to demonstrate its feasibility and validity in approximating solutions of low-dimensional partial differential equations with known solutions. We also explore the use of our JKO-ICNN approach in high dimensions with an experiment in controlled generation for molecular discovery.

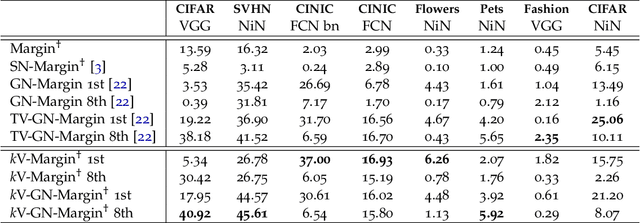
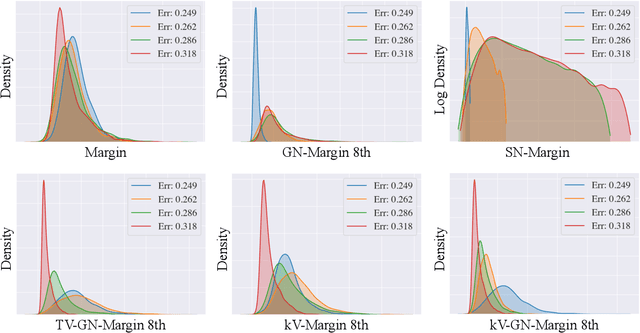
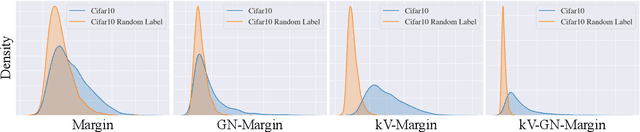
Measuring Generalization with Optimal Transport

Understanding the generalization of deep neural networks is one of the most important tasks in deep learning. Although much progress has been made, theoretical error bounds still often behave disparately from empirical observations. In this work, we develop margin-based generalization bounds, where the margins are normalized with optimal transport costs between independent random subsets sampled from the training distribution. In particular, the optimal transport cost can be interpreted as a generalization of variance which captures the structural properties of the learned feature space. Our bounds robustly predict the generalization error, given training data and network parameters, on large scale datasets. Theoretically, we demonstrate that the concentration and separation of features play crucial roles in generalization, supporting empirical results in the literature. The code is available at \url{https://github.com/chingyaoc/kV-Margin}.

Fair Mixup: Fairness via Interpolation

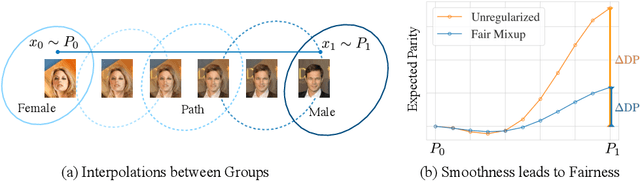
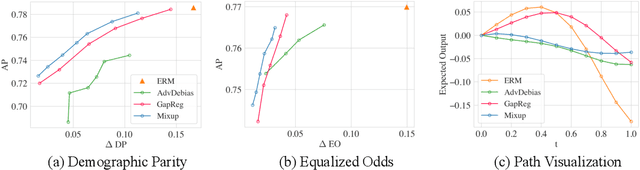
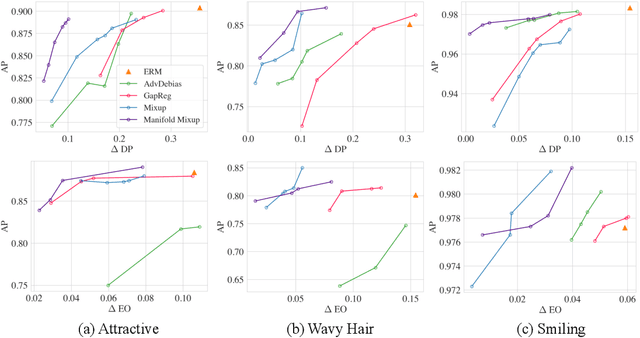
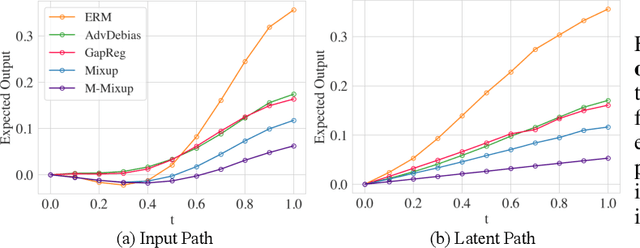
Training classifiers under fairness constraints such as group fairness, regularizes the disparities of predictions between the groups. Nevertheless, even though the constraints are satisfied during training, they might not generalize at evaluation time. To improve the generalizability of fair classifiers, we propose fair mixup, a new data augmentation strategy for imposing the fairness constraint. In particular, we show that fairness can be achieved by regularizing the models on paths of interpolated samples between the groups. We use mixup, a powerful data augmentation strategy to generate these interpolates. We analyze fair mixup and empirically show that it ensures a better generalization for both accuracy and fairness measurement in tabular, vision, and language benchmarks.

Image Captioning as an Assistive Technology: Lessons Learned from VizWiz 2020 Challenge

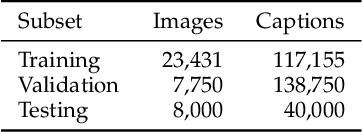
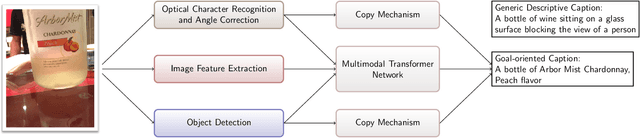
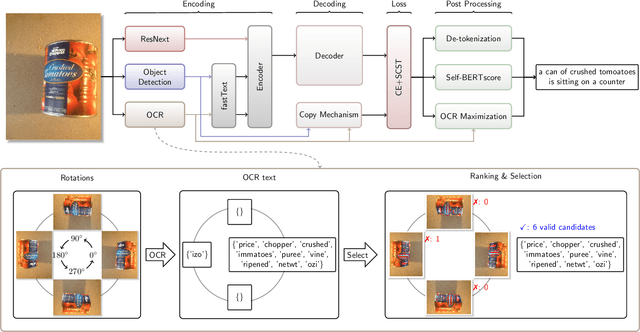
Image captioning has recently demonstrated impressive progress largely owing to the introduction of neural network algorithms trained on curated dataset like MS-COCO. Often work in this field is motivated by the promise of deployment of captioning systems in practical applications. However, the scarcity of data and contexts in many competition datasets renders the utility of systems trained on these datasets limited as an assistive technology in real-world settings, such as helping visually impaired people navigate and accomplish everyday tasks. This gap motivated the introduction of the novel VizWiz dataset, which consists of images taken by the visually impaired and captions that have useful, task-oriented information. In an attempt to help the machine learning computer vision field realize its promise of producing technologies that have positive social impact, the curators of the VizWiz dataset host several competitions, including one for image captioning. This work details the theory and engineering from our winning submission to the 2020 captioning competition. Our work provides a step towards improved assistive image captioning systems.

Alleviating Noisy Data in Image Captioning with Cooperative Distillation

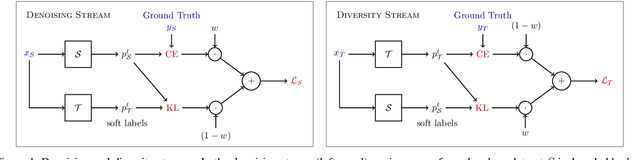
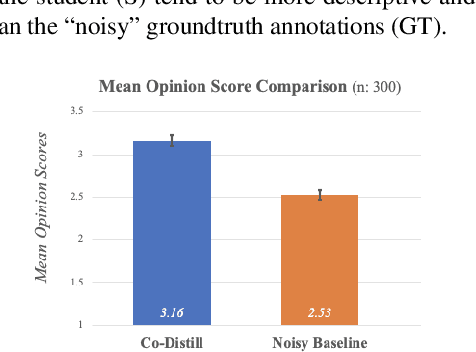
Image captioning systems have made substantial progress, largely due to the availability of curated datasets like Microsoft COCO or Vizwiz that have accurate descriptions of their corresponding images. Unfortunately, scarce availability of such cleanly labeled data results in trained algorithms producing captions that can be terse and idiosyncratically specific to details in the image. We propose a new technique, cooperative distillation that combines clean curated datasets with the web-scale automatically extracted captions of the Google Conceptual Captions dataset (GCC), which can have poor descriptions of images, but is abundant in size and therefore provides a rich vocabulary resulting in more expressive captions.

On the Convergence of Gradient Descent in GANs: MMD GAN As a Gradient Flow

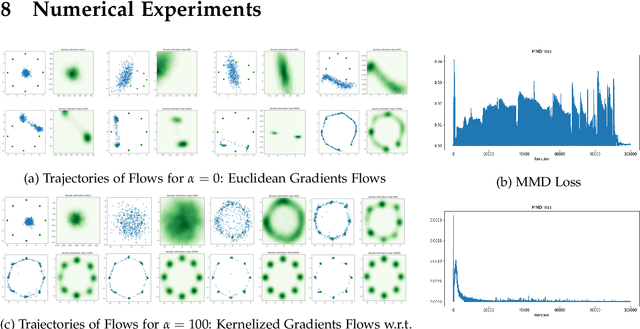
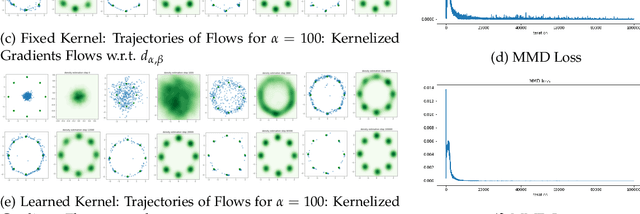
We consider the maximum mean discrepancy ($\mathrm{MMD}$) GAN problem and propose a parametric kernelized gradient flow that mimics the min-max game in gradient regularized $\mathrm{MMD}$ GAN. We show that this flow provides a descent direction minimizing the $\mathrm{MMD}$ on a statistical manifold of probability distributions. We then derive an explicit condition which ensures that gradient descent on the parameter space of the generator in gradient regularized $\mathrm{MMD}$ GAN is globally convergent to the target distribution. Under this condition, we give non asymptotic convergence results of gradient descent in MMD GAN. Another contribution of this paper is the introduction of a dynamic formulation of a regularization of $\mathrm{MMD}$ and demonstrating that the parametric kernelized descent for $\mathrm{MMD}$ is the gradient flow of this functional with respect to the new Riemannian structure. Our obtained theoretical result allows ones to treat gradient flows for quite general functionals and thus has potential applications to other types of variational inferences on a statistical manifold beyond GANs. Finally, numerical experiments suggest that our parametric kernelized gradient flow stabilizes GAN training and guarantees convergence.

Tabular Transformers for Modeling Multivariate Time Series

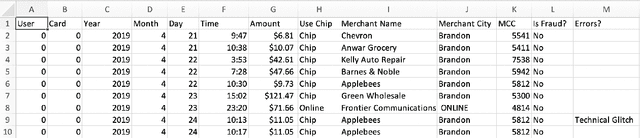
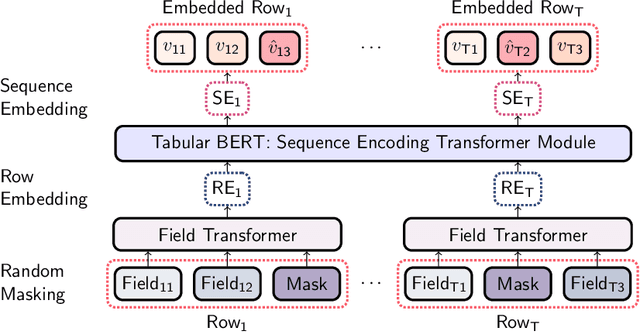
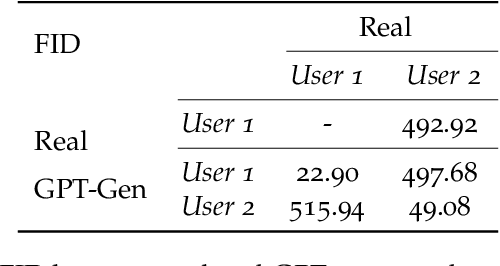
Tabular datasets are ubiquitous in data science applications. Given their importance, it seems natural to apply state-of-the-art deep learning algorithms in order to fully unlock their potential. Here we propose neural network models that represent tabular time series that can optionally leverage their hierarchical structure. This results in two architectures for tabular time series: one for learning representations that is analogous to BERT and can be pre-trained end-to-end and used in downstream tasks, and one that is akin to GPT and can be used for generation of realistic synthetic tabular sequences. We demonstrate our models on two datasets: a synthetic credit card transaction dataset, where the learned representations are used for fraud detection and synthetic data generation, and on a real pollution dataset, where the learned encodings are used to predict atmospheric pollutant concentrations. Code and data are available at https://github.com/IBM/TabFormer.

Unbalanced Sobolev Descent

We introduce Unbalanced Sobolev Descent (USD), a particle descent algorithm for transporting a high dimensional source distribution to a target distribution that does not necessarily have the same mass. We define the Sobolev-Fisher discrepancy between distributions and show that it relates to advection-reaction transport equations and the Wasserstein-Fisher-Rao metric between distributions. USD transports particles along gradient flows of the witness function of the Sobolev-Fisher discrepancy (advection step) and reweighs the mass of particles with respect to this witness function (reaction step). The reaction step can be thought of as a birth-death process of the particles with rate of growth proportional to the witness function. When the Sobolev-Fisher witness function is estimated in a Reproducing Kernel Hilbert Space (RKHS), under mild assumptions we show that USD converges asymptotically (in the limit of infinite particles) to the target distribution in the Maximum Mean Discrepancy (MMD) sense. We then give two methods to estimate the Sobolev-Fisher witness with neural networks, resulting in two Neural USD algorithms. The first one implements the reaction step with mirror descent on the weights, while the second implements it through a birth-death process of particles. We show on synthetic examples that USD transports distributions with or without conservation of mass faster than previous particle descent algorithms, and finally demonstrate its use for molecular biology analyses where our method is naturally suited to match developmental stages of populations of differentiating cells based on their single-cell RNA sequencing profile. Code is available at https://github.com/ibm/usd .