Assessing and improving reliability of neighbor embedding methods: a map-continuity perspective

Visualizing high-dimensional data is an important routine for understanding biomedical data and interpreting deep learning models. Neighbor embedding methods, such as t-SNE, UMAP, and LargeVis, among others, are a family of popular visualization methods which reduce high-dimensional data to two dimensions. However, recent studies suggest that these methods often produce visual artifacts, potentially leading to incorrect scientific conclusions. Recognizing that the current limitation stems from a lack of data-independent notions of embedding maps, we introduce a novel conceptual and computational framework, LOO-map, that learns the embedding maps based on a classical statistical idea known as the leave-one-out. LOO-map extends the embedding over a discrete set of input points to the entire input space, enabling a systematic assessment of map continuity, and thus the reliability of the visualizations. We find for many neighbor embedding methods, their embedding maps can be intrinsically discontinuous. The discontinuity induces two types of observed map distortion: ``overconfidence-inducing discontinuity," which exaggerates cluster separation, and ``fracture-inducing discontinuity," which creates spurious local structures. Building upon LOO-map, we propose two diagnostic point-wise scores -- perturbation score and singularity score -- to address these limitations. These scores can help identify unreliable embedding points, detect out-of-distribution data, and guide hyperparameter selection. Our approach is flexible and works as a wrapper around many neighbor embedding algorithms. We test our methods across multiple real-world datasets from computer vision and single-cell omics to demonstrate their effectiveness in enhancing the interpretability and accuracy of visualizations.

How does Multi-Task Training Affect Transformer In-Context Capabilities? Investigations with Function Classes

Large language models (LLM) have recently shown the extraordinary ability to perform unseen tasks based on few-shot examples provided as text, also known as in-context learning (ICL). While recent works have attempted to understand the mechanisms driving ICL, few have explored training strategies that incentivize these models to generalize to multiple tasks. Multi-task learning (MTL) for generalist models is a promising direction that offers transfer learning potential, enabling large parameterized models to be trained from simpler, related tasks. In this work, we investigate the combination of MTL with ICL to build models that efficiently learn tasks while being robust to out-of-distribution examples. We propose several effective curriculum learning strategies that allow ICL models to achieve higher data efficiency and more stable convergence. Our experiments reveal that ICL models can effectively learn difficult tasks by training on progressively harder tasks while mixing in prior tasks, denoted as mixed curriculum in this work. Our code and models are available at https://github.com/harmonbhasin/curriculum_learning_icl .

Uncovering hidden geometry in Transformers via disentangling position and context

Transformers are widely used to extract complex semantic meanings from input tokens, yet they usually operate as black-box models. In this paper, we present a simple yet informative decomposition of hidden states (or embeddings) of trained transformers into interpretable components. For any layer, embedding vectors of input sequence samples are represented by a tensor $\boldsymbol{h} \in \mathbb{R}^{C \times T \times d}$. Given embedding vector $\boldsymbol{h}_{c,t} \in \mathbb{R}^d$ at sequence position $t \le T$ in a sequence (or context) $c \le C$, extracting the mean effects yields the decomposition \[ \boldsymbol{h}_{c,t} = \boldsymbol{\mu} + \mathbf{pos}_t + \mathbf{ctx}_c + \mathbf{resid}_{c,t} \] where $\boldsymbol{\mu}$ is the global mean vector, $\mathbf{pos}_t$ and $\mathbf{ctx}_c$ are the mean vectors across contexts and across positions respectively, and $\mathbf{resid}_{c,t}$ is the residual vector. For popular transformer architectures and diverse text datasets, empirically we find pervasive mathematical structure: (1) $(\mathbf{pos}_t)_{t}$ forms a low-dimensional, continuous, and often spiral shape across layers, (2) $(\mathbf{ctx}_c)_c$ shows clear cluster structure that falls into context topics, and (3) $(\mathbf{pos}_t)_{t}$ and $(\mathbf{ctx}_c)_c$ are mutually incoherent -- namely $\mathbf{pos}_t$ is almost orthogonal to $\mathbf{ctx}_c$ -- which is canonical in compressed sensing and dictionary learning. This decomposition offers structural insights about input formats in in-context learning (especially for induction heads) and in arithmetic tasks.

Unraveling Projection Heads in Contrastive Learning: Insights from Expansion and Shrinkage

We investigate the role of projection heads, also known as projectors, within the encoder-projector framework (e.g., SimCLR) used in contrastive learning. We aim to demystify the observed phenomenon where representations learned before projectors outperform those learned after -- measured using the downstream linear classification accuracy, even when the projectors themselves are linear. In this paper, we make two significant contributions towards this aim. Firstly, through empirical and theoretical analysis, we identify two crucial effects -- expansion and shrinkage -- induced by the contrastive loss on the projectors. In essence, contrastive loss either expands or shrinks the signal direction in the representations learned by an encoder, depending on factors such as the augmentation strength, the temperature used in contrastive loss, etc. Secondly, drawing inspiration from the expansion and shrinkage phenomenon, we propose a family of linear transformations to accurately model the projector's behavior. This enables us to precisely characterize the downstream linear classification accuracy in the high-dimensional asymptotic limit. Our findings reveal that linear projectors operating in the shrinkage (or expansion) regime hinder (or improve) the downstream classification accuracy. This provides the first theoretical explanation as to why (linear) projectors impact the downstream performance of learned representations. Our theoretical findings are further corroborated by extensive experiments on both synthetic data and real image data.

Tractability from overparametrization: The example of the negative perceptron

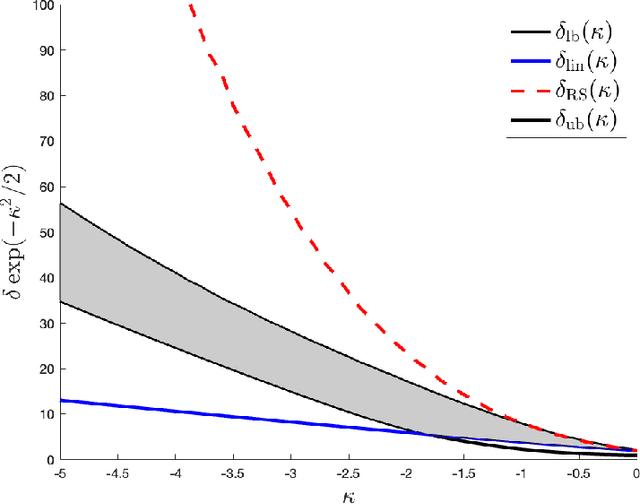
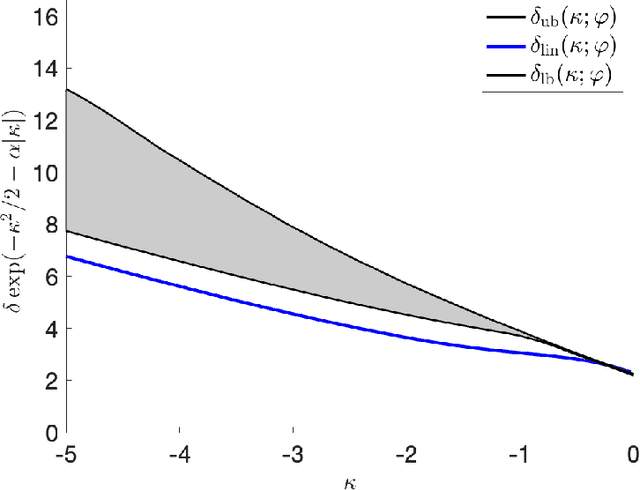
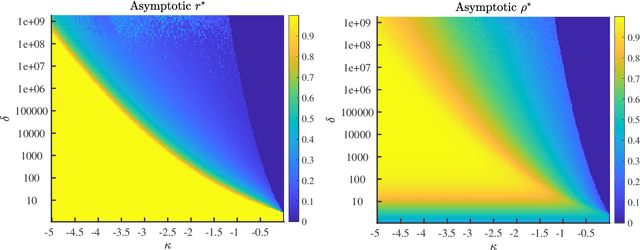
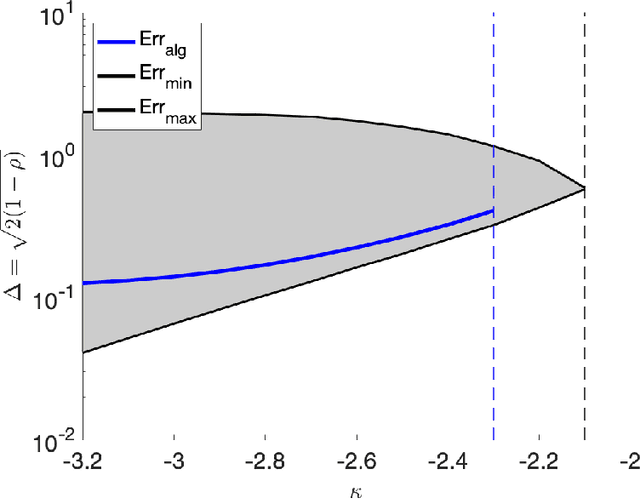
In the negative perceptron problem we are given $n$ data points $({\boldsymbol x}_i,y_i)$, where ${\boldsymbol x}_i$ is a $d$-dimensional vector and $y_i\in\{+1,-1\}$ is a binary label. The data are not linearly separable and hence we content ourselves to find a linear classifier with the largest possible \emph{negative} margin. In other words, we want to find a unit norm vector ${\boldsymbol \theta}$ that maximizes $\min_{i\le n}y_i\langle {\boldsymbol \theta},{\boldsymbol x}_i\rangle$. This is a non-convex optimization problem (it is equivalent to finding a maximum norm vector in a polytope), and we study its typical properties under two random models for the data. We consider the proportional asymptotics in which $n,d\to \infty$ with $n/d\to\delta$, and prove upper and lower bounds on the maximum margin $\kappa_{\text{s}}(\delta)$ or -- equivalently -- on its inverse function $\delta_{\text{s}}(\kappa)$. In other words, $\delta_{\text{s}}(\kappa)$ is the overparametrization threshold: for $n/d\le \delta_{\text{s}}(\kappa)-\varepsilon$ a classifier achieving vanishing training error exists with high probability, while for $n/d\ge \delta_{\text{s}}(\kappa)+\varepsilon$ it does not. Our bounds on $\delta_{\text{s}}(\kappa)$ match to the leading order as $\kappa\to -\infty$. We then analyze a linear programming algorithm to find a solution, and characterize the corresponding threshold $\delta_{\text{lin}}(\kappa)$. We observe a gap between the interpolation threshold $\delta_{\text{s}}(\kappa)$ and the linear programming threshold $\delta_{\text{lin}}(\kappa)$, raising the question of the behavior of other algorithms.

The Interpolation Phase Transition in Neural Networks: Memorization and Generalization under Lazy Training

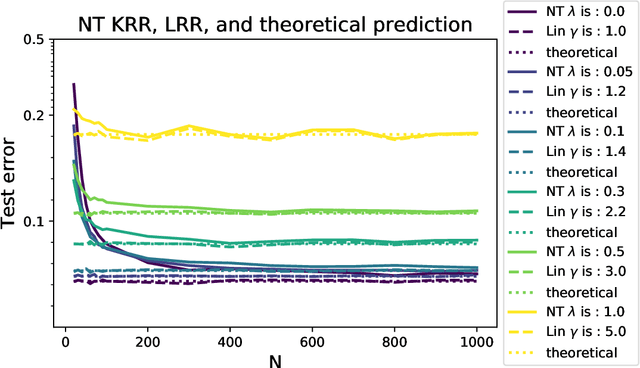
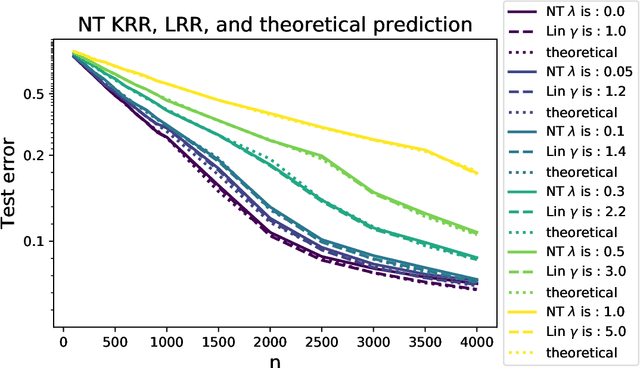
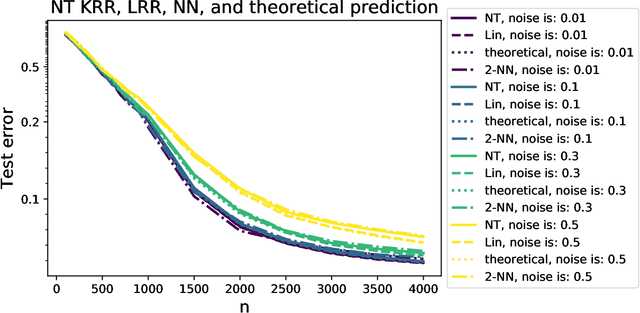
Modern neural networks are often operated in a strongly overparametrized regime: they comprise so many parameters that they can interpolate the training set, even if actual labels are replaced by purely random ones. Despite this, they achieve good prediction error on unseen data: interpolating the training set does not induce overfitting. Further, overparametrization appears to be beneficial in that it simplifies the optimization landscape. Here we study these phenomena in the context of two-layers neural networks in the neural tangent (NT) regime. We consider a simple data model, with isotropic feature vectors in $d$ dimensions, and $N$ hidden neurons. Under the assumption $N \le Cd$ (for $C$ a constant), we show that the network can exactly interpolate the data as soon as the number of parameters is significantly larger than the number of samples: $Nd\gg n$. Under these assumptions, we show that the empirical NT kernel has minimum eigenvalue bounded away from zero, and characterize the generalization error of min-$\ell_2$ norm interpolants, when the target function is linear. In particular, we show that the network approximately performs ridge regression in the raw features, with a strictly positive `self-induced' regularization.

A Selective Overview of Deep Learning

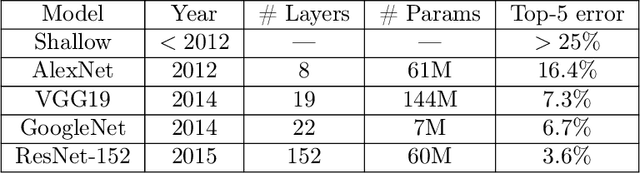
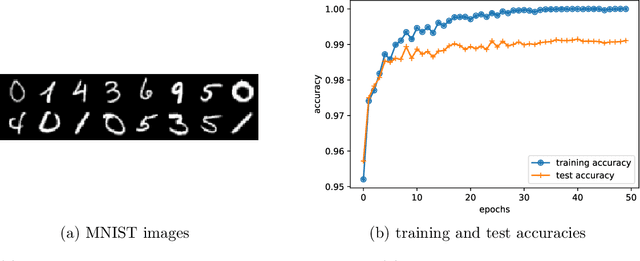
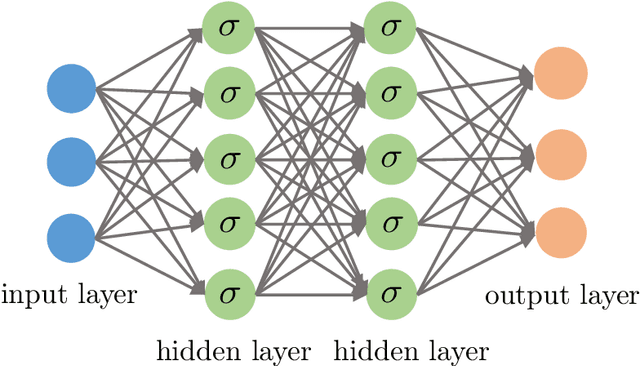
Deep learning has arguably achieved tremendous success in recent years. In simple words, deep learning uses the composition of many nonlinear functions to model the complex dependency between input features and labels. While neural networks have a long history, recent advances have greatly improved their performance in computer vision, natural language processing, etc. From the statistical and scientific perspective, it is natural to ask: What is deep learning? What are the new characteristics of deep learning, compared with classical methods? What are the theoretical foundations of deep learning? To answer these questions, we introduce common neural network models (e.g., convolutional neural nets, recurrent neural nets, generative adversarial nets) and training techniques (e.g., stochastic gradient descent, dropout, batch normalization) from a statistical point of view. Along the way, we highlight new characteristics of deep learning (including depth and over-parametrization) and explain their practical and theoretical benefits. We also sample recent results on theories of deep learning, many of which are only suggestive. While a complete understanding of deep learning remains elusive, we hope that our perspectives and discussions serve as a stimulus for new statistical research.

Robust high dimensional factor models with applications to statistical machine learning

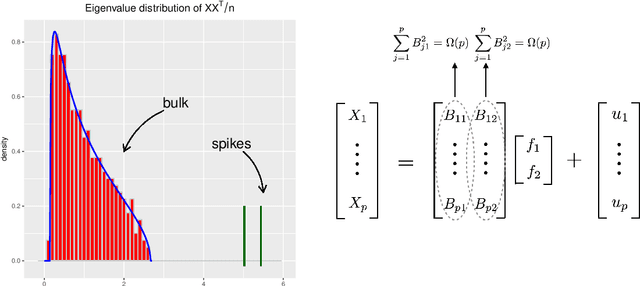
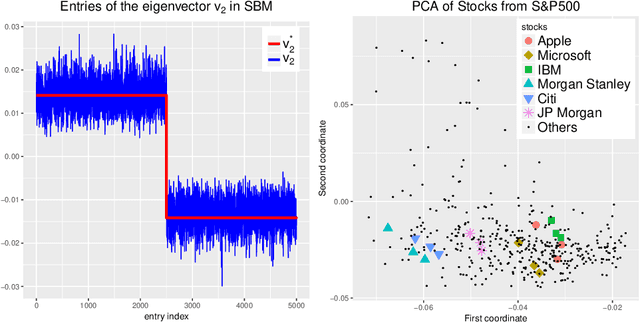
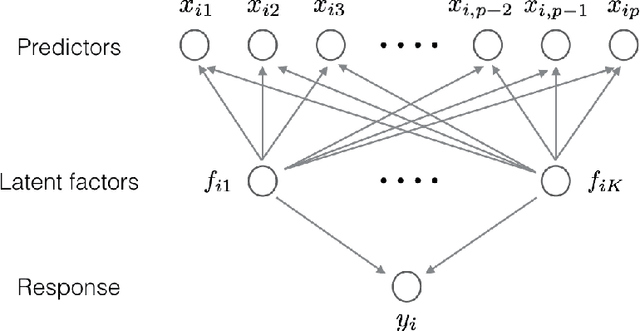
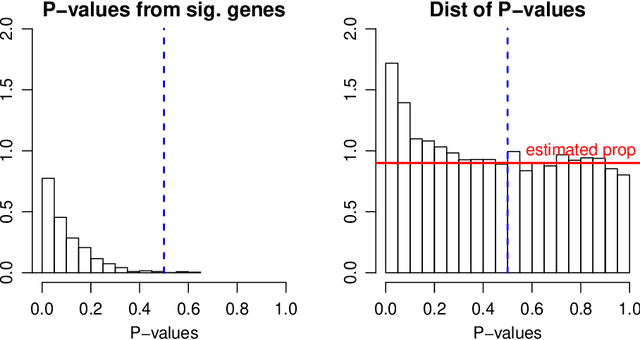
Factor models are a class of powerful statistical models that have been widely used to deal with dependent measurements that arise frequently from various applications from genomics and neuroscience to economics and finance. As data are collected at an ever-growing scale, statistical machine learning faces some new challenges: high dimensionality, strong dependence among observed variables, heavy-tailed variables and heterogeneity. High-dimensional robust factor analysis serves as a powerful toolkit to conquer these challenges. This paper gives a selective overview on recent advance on high-dimensional factor models and their applications to statistics including Factor-Adjusted Robust Model selection (FarmSelect) and Factor-Adjusted Robust Multiple testing (FarmTest). We show that classical methods, especially principal component analysis (PCA), can be tailored to many new problems and provide powerful tools for statistical estimation and inference. We highlight PCA and its connections to matrix perturbation theory, robust statistics, random projection, false discovery rate, etc., and illustrate through several applications how insights from these fields yield solutions to modern challenges. We also present far-reaching connections between factor models and popular statistical learning problems, including network analysis and low-rank matrix recovery.

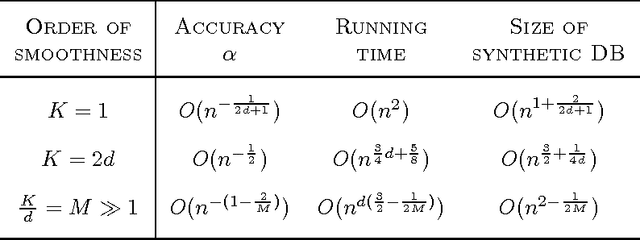
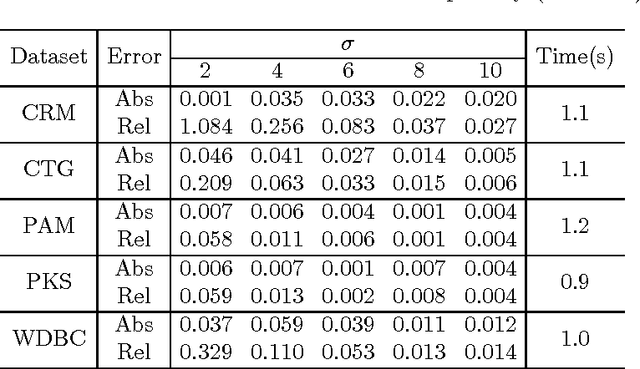
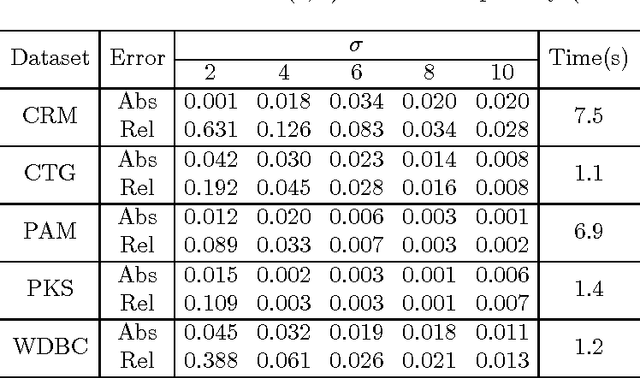
Differentially Private Data Releasing for Smooth Queries with Synthetic Database Output

We consider accurately answering smooth queries while preserving differential privacy. A query is said to be $K$-smooth if it is specified by a function defined on $[-1,1]^d$ whose partial derivatives up to order $K$ are all bounded. We develop an $\epsilon$-differentially private mechanism for the class of $K$-smooth queries. The major advantage of the algorithm is that it outputs a synthetic database. In real applications, a synthetic database output is appealing. Our mechanism achieves an accuracy of $O (n^{-\frac{K}{2d+K}}/\epsilon )$, and runs in polynomial time. We also generalize the mechanism to preserve $(\epsilon, \delta)$-differential privacy with slightly improved accuracy. Extensive experiments on benchmark datasets demonstrate that the mechanisms have good accuracy and are efficient.