Fast Projection onto the Capped Simplex with Applications to Sparse Regression in Bioinformatics

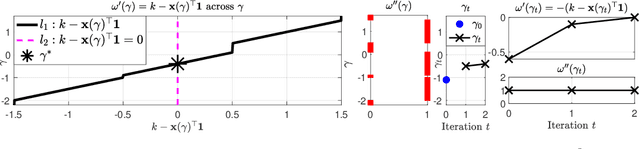
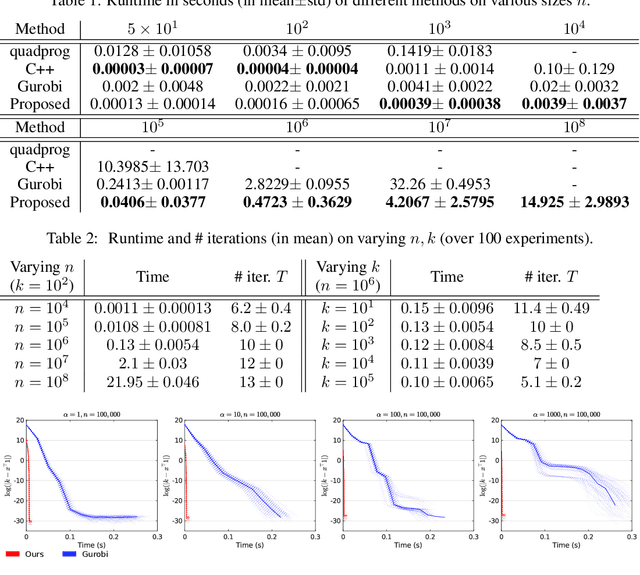
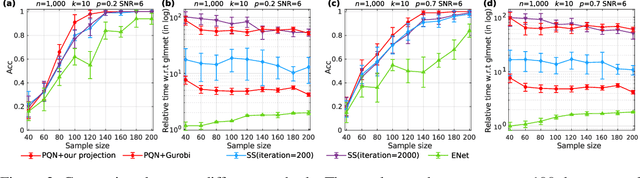
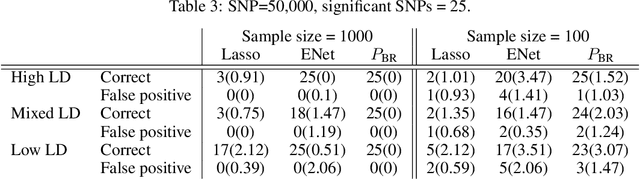
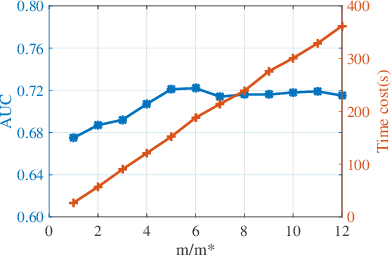
We consider the problem of projecting a vector onto the so-called k-capped simplex, which is a hyper-cube cut by a hyperplane. For an n-dimensional input vector with bounded elements, we found that a simple algorithm based on Newton's method is able to solve the projection problem to high precision with a complexity roughly about O(n), which has a much lower computational cost compared with the existing sorting-based methods proposed in the literature. We provide a theory for partial explanation and justification of the method. We demonstrate that the proposed algorithm can produce a solution of the projection problem with high precision on large scale datasets, and the algorithm is able to significantly outperform the state-of-the-art methods in terms of runtime (about 6-8 times faster than a commercial software with respect to CPU time for input vector with 1 million variables or more). We further illustrate the effectiveness of the proposed algorithm on solving sparse regression in a bioinformatics problem. Empirical results on the GWAS dataset (with 1,500,000 single-nucleotide polymorphisms) show that, when using the proposed method to accelerate the Projected Quasi-Newton (PQN) method, the accelerated PQN algorithm is able to handle huge-scale regression problem and it is more efficient (about 3-6 times faster) than the current state-of-the-art methods.

DRAM Failure Prediction in AIOps: Empirical Evaluation, Challenges and Opportunities

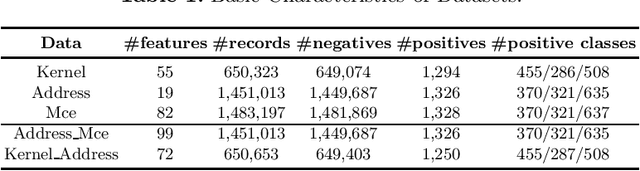
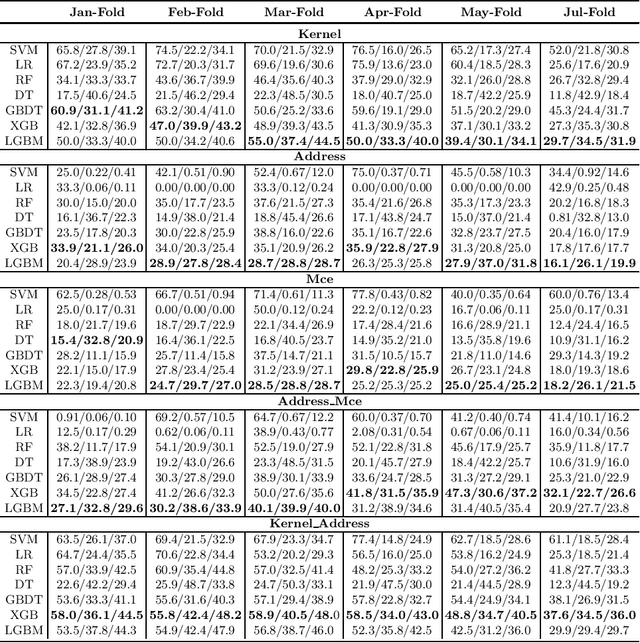
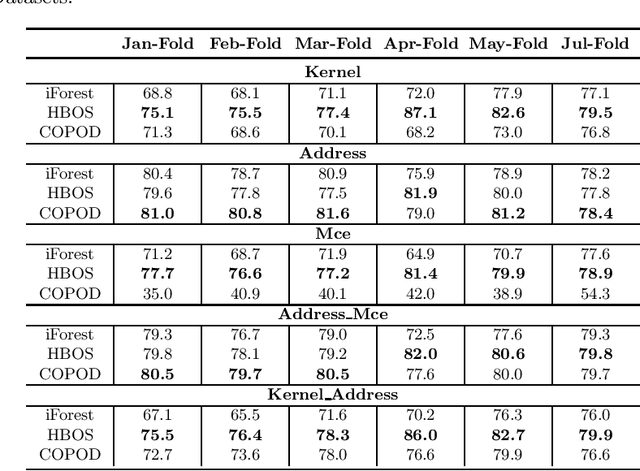
DRAM failure prediction is a vital task in AIOps, which is crucial to maintain the reliability and sustainable service of large-scale data centers. However, limited work has been done on DRAM failure prediction mainly due to the lack of public available datasets. This paper presents a comprehensive empirical evaluation of diverse machine learning techniques for DRAM failure prediction using a large-scale multi-source dataset, including more than three millions of records of kernel, address, and mcelog data, provided by Alibaba Cloud through PAKDD 2021 competition. Particularly, we first formulate the problem as a multi-class classification task and exhaustively evaluate seven popular/state-of-the-art classifiers on both the individual and multiple data sources. We then formulate the problem as an unsupervised anomaly detection task and evaluate three state-of-the-art anomaly detectors. Further, based on the empirical results and our experience of attending this competition, we discuss major challenges and present future research opportunities in this task.

Wasserstein Robust Support Vector Machines with Fairness Constraints

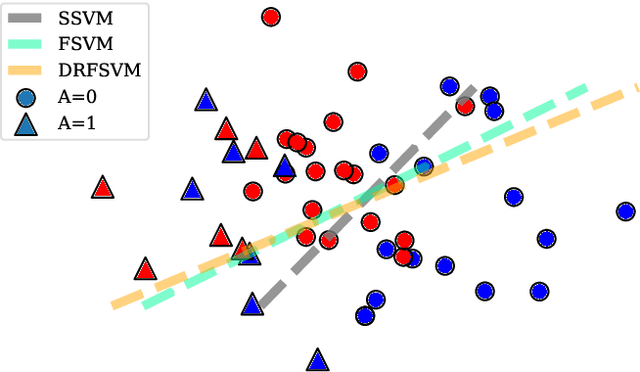
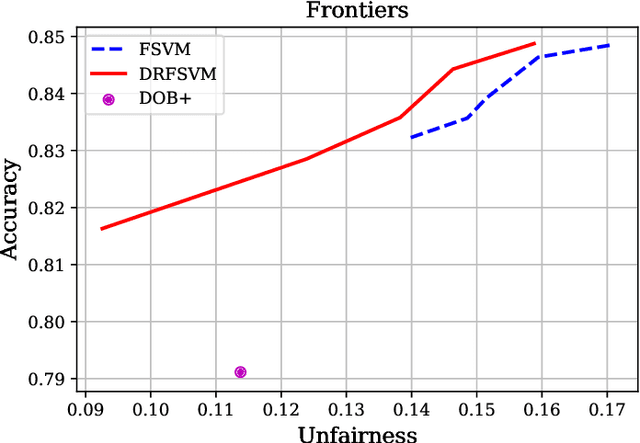
We propose a distributionally robust support vector machine with a fairness constraint that encourages the classifier to be fair in view of the equality of opportunity criterion. We use a type-$\infty$ Wasserstein ambiguity set centered at the empirical distribution to model distributional uncertainty and derive an exact reformulation for worst-case unfairness measure. We establish that the model is equivalent to a mixed-binary optimization problem, which can be solved by standard off-the-shelf solvers. We further prove that the expectation of the hinge loss objective function constitutes an upper bound on the misclassification probability. Finally, we numerically demonstrate that our proposed approach improves fairness with negligible loss of predictive accuracy.

Outlier Detection Ensemble with Embedded Feature Selection

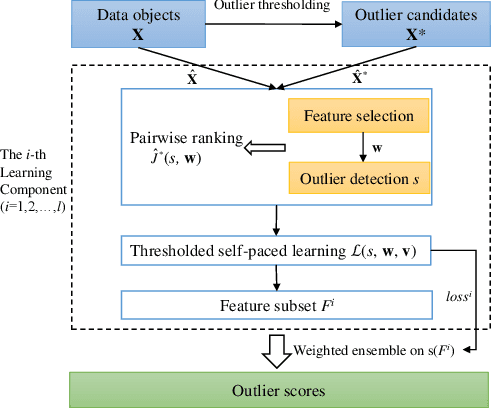
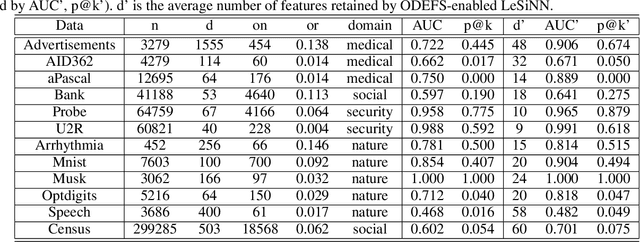
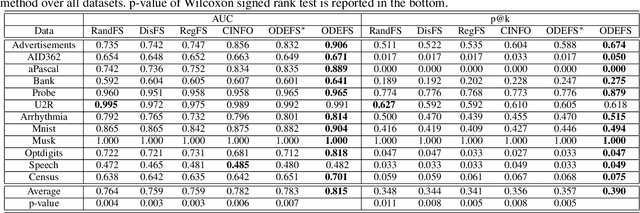
Feature selection places an important role in improving the performance of outlier detection, especially for noisy data. Existing methods usually perform feature selection and outlier scoring separately, which would select feature subsets that may not optimally serve for outlier detection, leading to unsatisfying performance. In this paper, we propose an outlier detection ensemble framework with embedded feature selection (ODEFS), to address this issue. Specifically, for each random sub-sampling based learning component, ODEFS unifies feature selection and outlier detection into a pairwise ranking formulation to learn feature subsets that are tailored for the outlier detection method. Moreover, we adopt the thresholded self-paced learning to simultaneously optimize feature selection and example selection, which is helpful to improve the reliability of the training set. After that, we design an alternate algorithm with proved convergence to solve the resultant optimization problem. In addition, we analyze the generalization error bound of the proposed framework, which provides theoretical guarantee on the method and insightful practical guidance. Comprehensive experimental results on 12 real-world datasets from diverse domains validate the superiority of the proposed ODEFS.

HPLFlowNet: Hierarchical Permutohedral Lattice FlowNet for Scene Flow Estimation on Large-scale Point Clouds

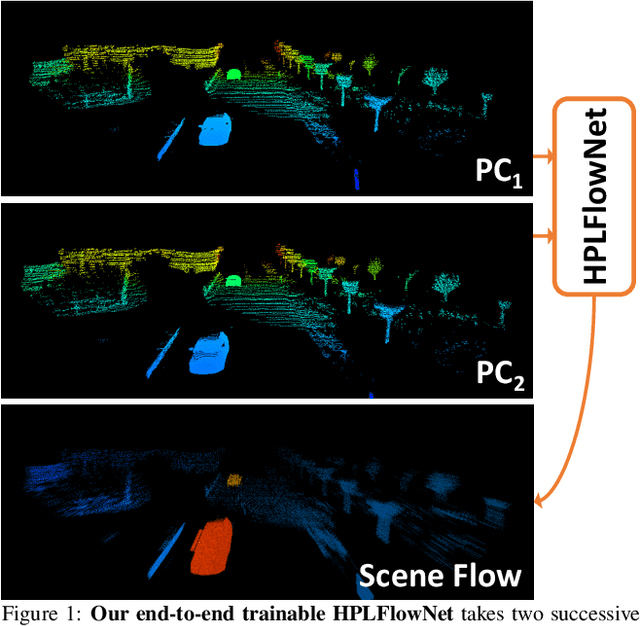
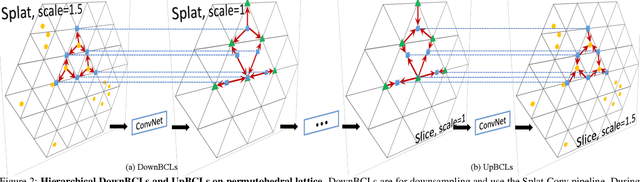
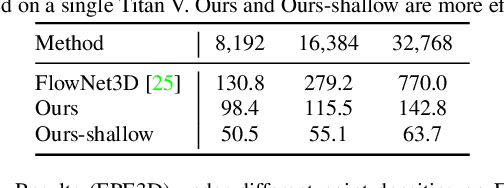
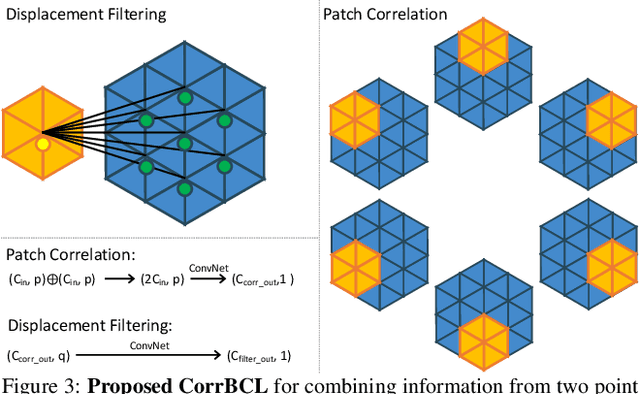
We present a novel deep neural network architecture for end-to-end scene flow estimation that directly operates on large-scale 3D point clouds. Inspired by Bilateral Convolutional Layers (BCL), we propose novel DownBCL, UpBCL, and CorrBCL operations that restore structural information from unstructured point clouds, and fuse information from two consecutive point clouds. Operating on discrete and sparse permutohedral lattice points, our architectural design is parsimonious in computational cost. Our model can efficiently process a pair of point cloud frames at once with a maximum of 86K points per frame. Our approach achieves state-of-the-art performance on the FlyingThings3D and KITTI Scene Flow 2015 datasets. Moreover, trained on synthetic data, our approach shows great generalization ability on real-world data and on different point densities without fine-tuning.