Adaptive Rollout Allocation for Online Reinforcement Learning with Verifiable Rewards

Sampling efficiency is a key bottleneck in reinforcement learning with verifiable rewards. Existing group-based policy optimization methods, such as GRPO, allocate a fixed number of rollouts for all training prompts. This uniform allocation implicitly treats all prompts as equally informative, and could lead to inefficient computational budget usage and impede training progress. We introduce VIP, a Variance-Informed Predictive allocation strategy that allocates a given rollout budget to the prompts in the incumbent batch to minimize the expected gradient variance of the policy update. At each iteration, VIP uses a lightweight Gaussian process model to predict per-prompt success probabilities based on recent rollouts. These probability predictions are translated into variance estimates, which are then fed into a convex optimization problem to determine the optimal rollout allocations under a hard compute budget constraint. Empirical results show that VIP consistently improves sampling efficiency and achieves higher performance than uniform or heuristic allocation strategies in multiple benchmarks.

Provably Data-driven Multiple Hyper-parameter Tuning with Structured Loss Function

Data-driven algorithm design automates hyperparameter tuning, but its statistical foundations remain limited because model performance can depend on hyperparameters in implicit and highly non-smooth ways. Existing guarantees focus on the simple case of a one-dimensional (scalar) hyperparameter. This leaves the practically important, multi-dimensional hyperparameter tuning setting unresolved. We address this open question by establishing the first general framework for establishing generalization guarantees for tuning multi-dimensional hyperparameters in data-driven settings. Our approach strengthens the generalization guarantee framework for semi-algebraic function classes by exploiting tools from real algebraic geometry, yielding sharper, more broadly applicable guarantees. We then extend the analysis to hyperparameter tuning using the validation loss under minimal assumptions, and derive improved bounds when additional structure is available. Finally, we demonstrate the scope of the framework with new learnability results, including data-driven weighted group lasso and weighted fused lasso.

Exploring Diverse Generation Paths via Inference-time Stiefel Activation Steering

Language models often default to a narrow set of high-probability outputs, leaving their generation paths homogeneous and prone to mode collapse. Sampling-based strategies inject randomness but still struggle to guarantee diversity across multiple concurrent generation runs. We address this limitation by introducing STARS ($\textbf{St}$iefel-based $\textbf{A}$ctivation Steering for Diverse $\textbf{R}$ea$\textbf{S}$oning), a training-free, inference-time intervention method that transforms activation steering into an exploration engine. At each token, STARS collects the hidden activations of concurrent generation runs and optimizes multiple additive steering directions jointly on the Stiefel manifold. STARS maximizes the geometric volume of the steered activations, while the Stiefel manifold induces orthogonality of the steering interventions. This formulation explicitly promotes divergent activation vectors of concurrent generation runs, and implicitly promotes divergent generation trajectories. This manifold optimization formulation can be solved using a Riemannian gradient descent algorithm with convergence guarantees, but this algorithm is too time-consuming for real-time inference. To guarantee low latency, we further design a lightweight one-step update with an aggressive, closed-form stepsize. For test case generation and scientific discovery benchmarks, STARS consistently outperforms standard sampling methods, achieving greater diversity without sacrificing qualitative performance.

SCOPE: Spectral Concentration by Distributionally Robust Joint Covariance-Precision Estimation

We propose a distributionally robust formulation for simultaneously estimating the covariance matrix and the precision matrix of a random vector.The proposed model minimizes the worst-case weighted sum of the Frobenius loss of the covariance estimator and Stein's loss of the precision matrix estimator against all distributions from an ambiguity set centered at the nominal distribution. The radius of the ambiguity set is measured via convex spectral divergence. We demonstrate that the proposed distributionally robust estimation model can be reduced to a convex optimization problem, thereby yielding quasi-analytical estimators. The joint estimators are shown to be nonlinear shrinkage estimators. The eigenvalues of the estimators are shrunk nonlinearly towards a positive scalar, where the scalar is determined by the weight coefficient of the loss terms. By tuning the coefficient carefully, the shrinkage corrects the spectral bias of the empirical covariance/precision matrix estimator. By this property, we call the proposed joint estimator the Spectral concentrated COvariance and Precision matrix Estimator (SCOPE). We demonstrate that the shrinkage effect improves the condition number of the estimator. We provide a parameter-tuning scheme that adjusts the shrinkage target and intensity that is asymptotically optimal. Numerical experiments on synthetic and real data show that our shrinkage estimators perform competitively against state-of-the-art estimators in practical applications.

Test-time Diverse Reasoning by Riemannian Activation Steering

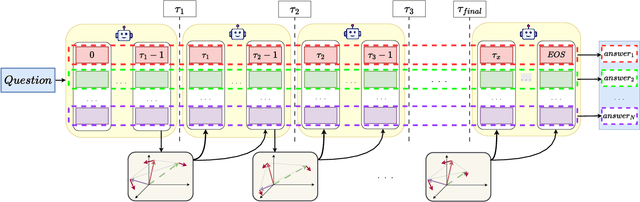
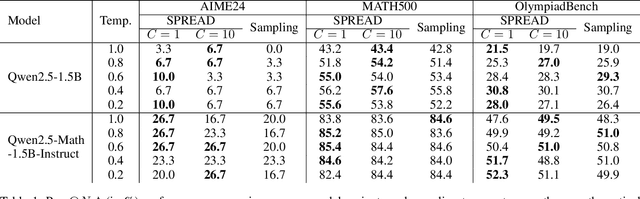
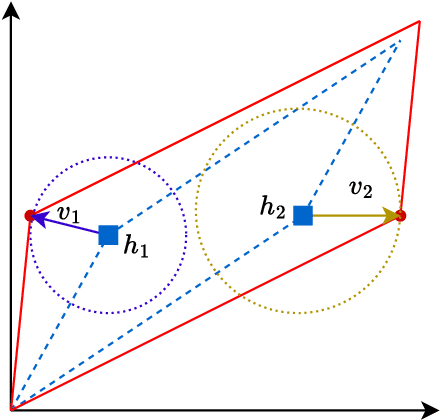
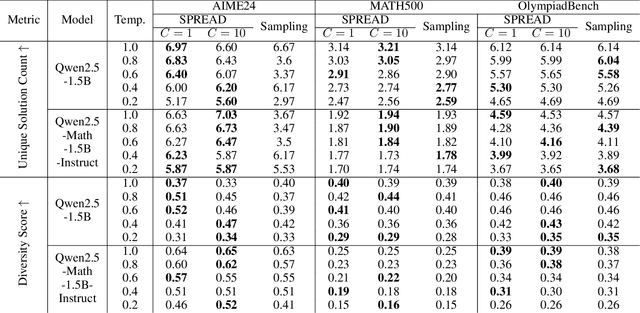
Best-of-$N$ reasoning improves the accuracy of language models in solving complex tasks by sampling multiple candidate solutions and then selecting the best one based on some criteria. A critical bottleneck for this strategy is the output diversity limit, which occurs when the model generates similar outputs despite stochastic sampling, and hence recites the same error. To address this lack of variance in reasoning paths, we propose a novel unsupervised activation steering strategy that simultaneously optimizes the steering vectors for multiple reasoning trajectories at test time. At any synchronization anchor along the batch generation process, we find the steering vectors that maximize the total volume spanned by all possible intervened activation subsets. We demonstrate that these steering vectors can be determined by solving a Riemannian optimization problem over the product of spheres with a log-determinant objective function. We then use a Riemannian block-coordinate descent algorithm with a well-tuned learning rate to obtain a stationary point of the problem, and we apply these steering vectors until the generation process reaches the subsequent synchronization anchor. Empirical evaluations on popular mathematical benchmarks demonstrate that our test-time Riemannian activation steering strategy outperforms vanilla sampling techniques in terms of generative diversity and solution accuracy.

Structured Pruning for Diverse Best-of-N Reasoning Optimization

Model pruning in transformer-based language models, traditionally viewed as a means of achieving computational savings, can enhance the model's reasoning capabilities. In this work, we uncover a surprising phenomenon: the selective pruning of certain attention heads leads to improvements in reasoning performance, particularly on challenging tasks. Motivated by this observation, we propose SPRINT, a novel contrastive learning framework that dynamically selects the optimal head and layer to prune during inference. By aligning question embeddings with head embeddings, SPRINT identifies those pruned-head configurations that result in more accurate reasoning. Extensive experiments demonstrate that our method significantly outperforms traditional best-of-$N$ and random head selection strategies on the MATH500 and GSM8K datasets.

Mixture-of-Personas Language Models for Population Simulation

Advances in Large Language Models (LLMs) paved the way for their emerging applications in various domains, such as human behavior simulations, where LLMs could augment human-generated data in social science research and machine learning model training. However, pretrained LLMs often fail to capture the behavioral diversity of target populations due to the inherent variability across individuals and groups. To address this, we propose \textit{Mixture of Personas} (MoP), a \textit{probabilistic} prompting method that aligns the LLM responses with the target population. MoP is a contextual mixture model, where each component is an LM agent characterized by a persona and an exemplar representing subpopulation behaviors. The persona and exemplar are randomly chosen according to the learned mixing weights to elicit diverse LLM responses during simulation. MoP is flexible, requires no model finetuning, and is transferable across base models. Experiments for synthetic data generation show that MoP outperforms competing methods in alignment and diversity metrics.

Task-driven Layerwise Additive Activation Intervention

Modern language models (LMs) have significantly advanced generative modeling in natural language processing (NLP). Despite their success, LMs often struggle with adaptation to new contexts in real-time applications. A promising approach to task adaptation is activation intervention, which steers the LMs' generation process by identifying and manipulating the activations. However, existing interventions are highly dependent on heuristic rules or require many prompt inputs to determine effective interventions. This paper proposes a layer-wise additive activation intervention framework that optimizes the intervention process, thus enhancing the sample efficiency. We benchmark our framework on various datasets, demonstrating improvements in the accuracy of pre-trained LMs and competing intervention baselines.

Probe-Free Low-Rank Activation Intervention

Language models (LMs) can produce texts that appear accurate and coherent but contain untruthful or toxic content. Inference-time interventions that edit the hidden activations have shown promising results in steering the LMs towards desirable generations. Existing activation intervention methods often comprise an activation probe to detect undesirable generation, triggering the activation modification to steer subsequent generation. This paper proposes a probe-free intervention method FLORAIN for all attention heads in a specific activation layer. It eliminates the need to train classifiers for probing purposes. The intervention function is parametrized by a sample-wise nonlinear low-rank mapping, which is trained by minimizing the distance between the modified activations and their projection onto the manifold of desirable content. Under specific constructions of the manifold and projection distance, we show that the intervention strategy can be computed efficiently by solving a smooth optimization problem. The empirical results, benchmarked on multiple base models, demonstrate that FLORAIN consistently outperforms several baseline methods in enhancing model truthfulness and quality across generation and multiple-choice tasks.

Risk-Aware Distributional Intervention Policies for Language Models

Language models are prone to occasionally undesirable generations, such as harmful or toxic content, despite their impressive capability to produce texts that appear accurate and coherent. This paper presents a new two-stage approach to detect and mitigate undesirable content generations by rectifying activations. First, we train an ensemble of layerwise classifiers to detect undesirable content using activations by minimizing a smooth surrogate of the risk-aware score. Then, for contents that are detected as undesirable, we propose layerwise distributional intervention policies that perturb the attention heads minimally while guaranteeing probabilistically the effectiveness of the intervention. Benchmarks on several language models and datasets show that our method outperforms baselines in reducing the generation of undesirable output.