Neural Conservation Laws: A Divergence-Free Perspective

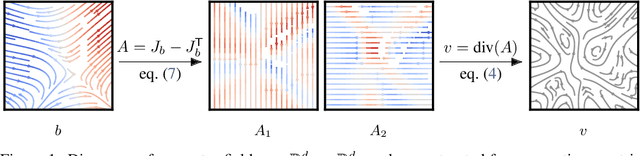
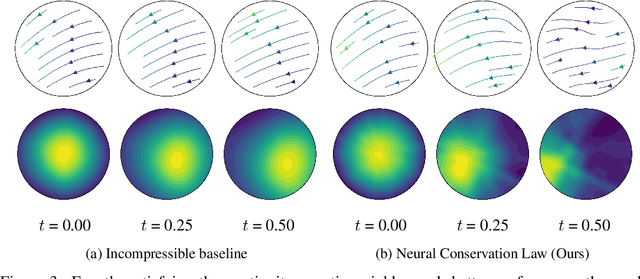
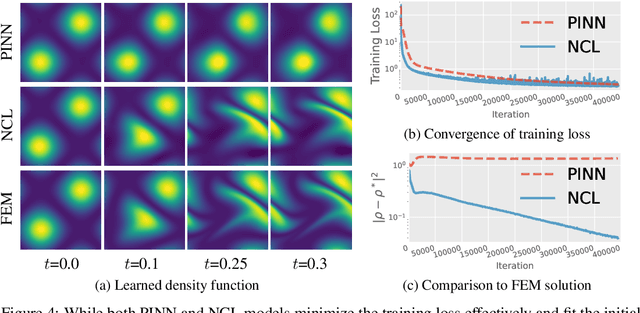
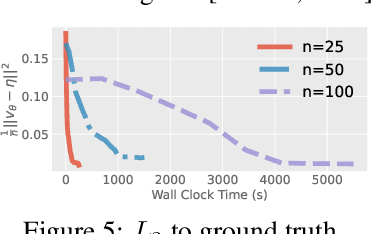
We investigate the parameterization of deep neural networks that by design satisfy the continuity equation, a fundamental conservation law. This is enabled by the observation that solutions of the continuity equation can be represented as a divergence-free vector field. We hence propose building divergence-free neural networks through the concept of differential forms, and with the aid of automatic differentiation, realize two practical constructions. As a result, we can parameterize pairs of densities and vector fields that always satisfy the continuity equation by construction, foregoing the need for extra penalty methods or expensive numerical simulation. Furthermore, we prove these models are universal and so can be used to represent any divergence-free vector field. Finally, we experimentally validate our approaches on neural network-based solutions to fluid equations, solving for the Hodge decomposition, and learning dynamical optimal transport maps the Hodge decomposition, and learning dynamical optimal transport maps.

Matching Normalizing Flows and Probability Paths on Manifolds

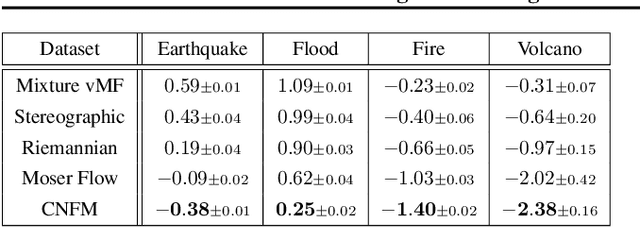
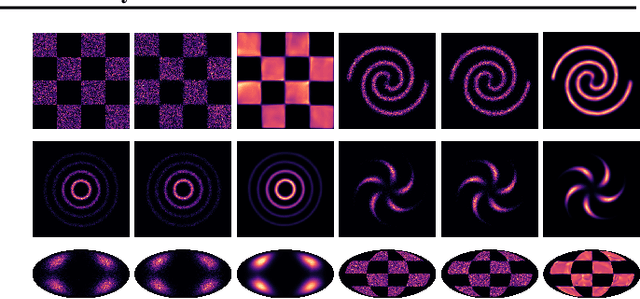
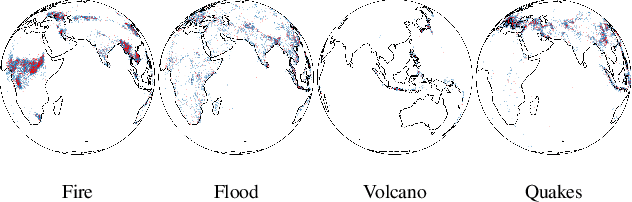
Continuous Normalizing Flows (CNFs) are a class of generative models that transform a prior distribution to a model distribution by solving an ordinary differential equation (ODE). We propose to train CNFs on manifolds by minimizing probability path divergence (PPD), a novel family of divergences between the probability density path generated by the CNF and a target probability density path. PPD is formulated using a logarithmic mass conservation formula which is a linear first order partial differential equation relating the log target probabilities and the CNF's defining vector field. PPD has several key benefits over existing methods: it sidesteps the need to solve an ODE per iteration, readily applies to manifold data, scales to high dimensions, and is compatible with a large family of target paths interpolating pure noise and data in finite time. Theoretically, PPD is shown to bound classical probability divergences. Empirically, we show that CNFs learned by minimizing PPD achieve state-of-the-art results in likelihoods and sample quality on existing low-dimensional manifold benchmarks, and is the first example of a generative model to scale to moderately high dimensional manifolds.

Weisfeiler and Leman go Machine Learning: The Story so far

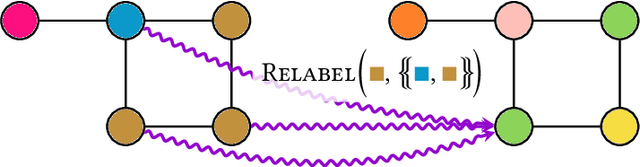
In recent years, algorithms and neural architectures based on the Weisfeiler-Leman algorithm, a well-known heuristic for the graph isomorphism problem, emerged as a powerful tool for machine learning with graphs and relational data. Here, we give a comprehensive overview of the algorithm's use in a machine learning setting, focusing on the supervised regime. We discuss the theoretical background, show how to use it for supervised graph- and node representation learning, discuss recent extensions, and outline the algorithm's connection to (permutation-)equivariant neural architectures. Moreover, we give an overview of current applications and future directions to stimulate further research.

Frame Averaging for Equivariant Shape Space Learning

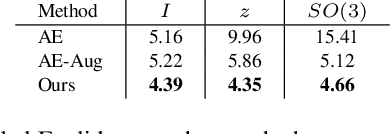
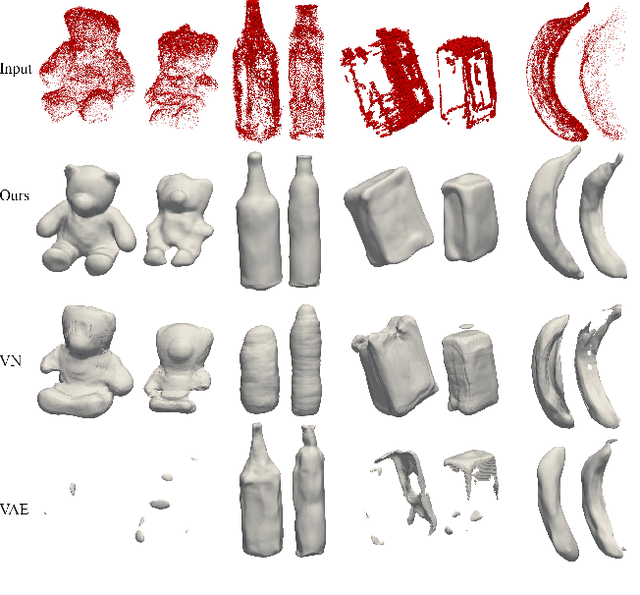
The task of shape space learning involves mapping a train set of shapes to and from a latent representation space with good generalization properties. Often, real-world collections of shapes have symmetries, which can be defined as transformations that do not change the essence of the shape. A natural way to incorporate symmetries in shape space learning is to ask that the mapping to the shape space (encoder) and mapping from the shape space (decoder) are equivariant to the relevant symmetries. In this paper, we present a framework for incorporating equivariance in encoders and decoders by introducing two contributions: (i) adapting the recent Frame Averaging (FA) framework for building generic, efficient, and maximally expressive Equivariant autoencoders; and (ii) constructing autoencoders equivariant to piecewise Euclidean motions applied to different parts of the shape. To the best of our knowledge, this is the first fully piecewise Euclidean equivariant autoencoder construction. Training our framework is simple: it uses standard reconstruction losses and does not require the introduction of new losses. Our architectures are built of standard (backbone) architectures with the appropriate frame averaging to make them equivariant. Testing our framework on both rigid shapes dataset using implicit neural representations, and articulated shape datasets using mesh-based neural networks show state-of-the-art generalization to unseen test shapes, improving relevant baselines by a large margin. In particular, our method demonstrates significant improvement in generalizing to unseen articulated poses.

Frame Averaging for Invariant and Equivariant Network Design

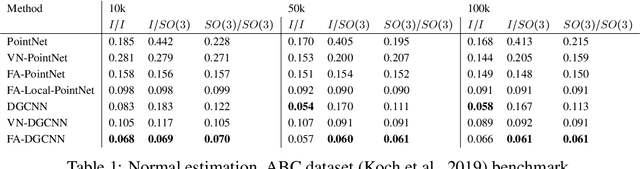
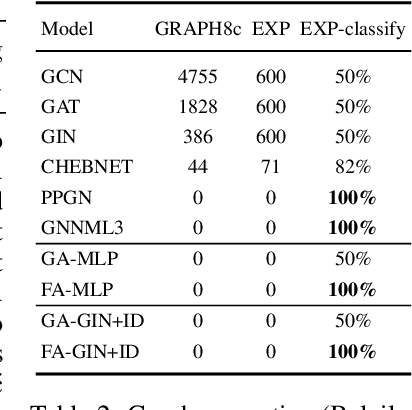
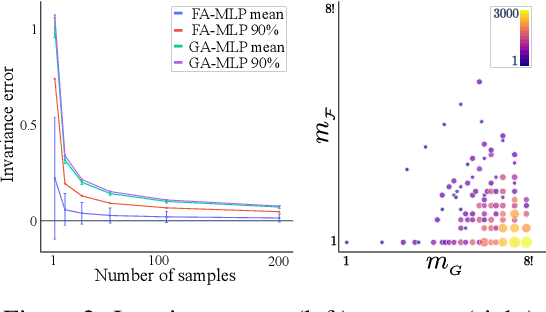
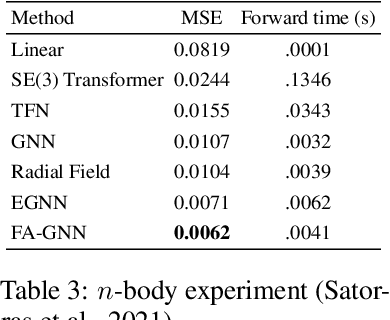
Many machine learning tasks involve learning functions that are known to be invariant or equivariant to certain symmetries of the input data. However, it is often challenging to design neural network architectures that respect these symmetries while being expressive and computationally efficient. For example, Euclidean motion invariant/equivariant graph or point cloud neural networks. We introduce Frame Averaging (FA), a general purpose and systematic framework for adapting known (backbone) architectures to become invariant or equivariant to new symmetry types. Our framework builds on the well known group averaging operator that guarantees invariance or equivariance but is intractable. In contrast, we observe that for many important classes of symmetries, this operator can be replaced with an averaging operator over a small subset of the group elements, called a frame. We show that averaging over a frame guarantees exact invariance or equivariance while often being much simpler to compute than averaging over the entire group. Furthermore, we prove that FA-based models have maximal expressive power in a broad setting and in general preserve the expressive power of their backbone architectures. Using frame averaging, we propose a new class of universal Graph Neural Networks (GNNs), universal Euclidean motion invariant point cloud networks, and Euclidean motion invariant Message Passing (MP) GNNs. We demonstrate the practical effectiveness of FA on several applications including point cloud normal estimation, beyond $2$-WL graph separation, and $n$-body dynamics prediction, achieving state-of-the-art results in all of these benchmarks.

Augmenting Implicit Neural Shape Representations with Explicit Deformation Fields

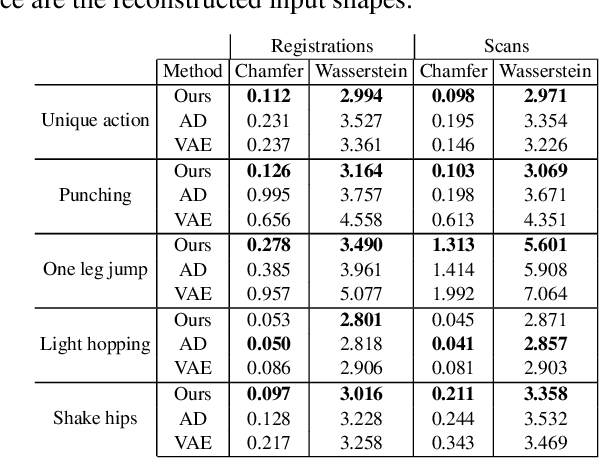
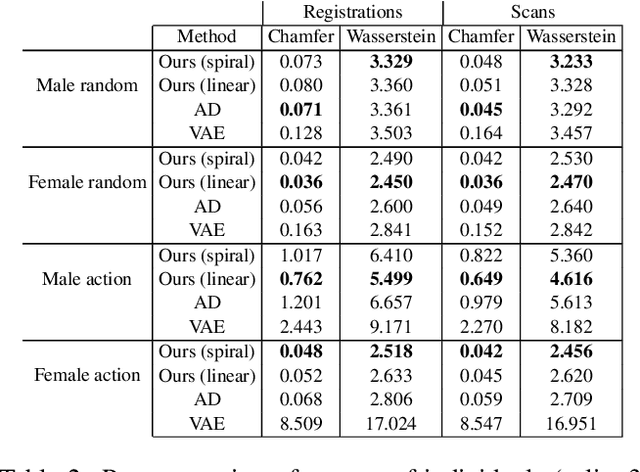
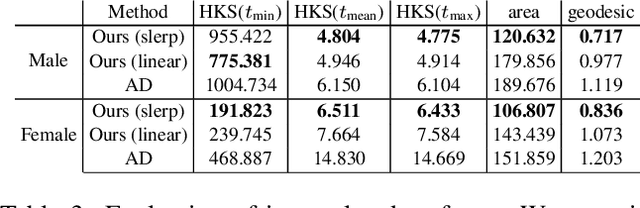
Implicit neural representation is a recent approach to learn shape collections as zero level-sets of neural networks, where each shape is represented by a latent code. So far, the focus has been shape reconstruction, while shape generalization was mostly left to generic encoder-decoder or auto-decoder regularization. In this paper we advocate deformation-aware regularization for implicit neural representations, aiming at producing plausible deformations as latent code changes. The challenge is that implicit representations do not capture correspondences between different shapes, which makes it difficult to represent and regularize their deformations. Thus, we propose to pair the implicit representation of the shapes with an explicit, piecewise linear deformation field, learned as an auxiliary function. We demonstrate that, by regularizing these deformation fields, we can encourage the implicit neural representation to induce natural deformations in the learned shape space, such as as-rigid-as-possible deformations.

Moser Flow: Divergence-based Generative Modeling on Manifolds

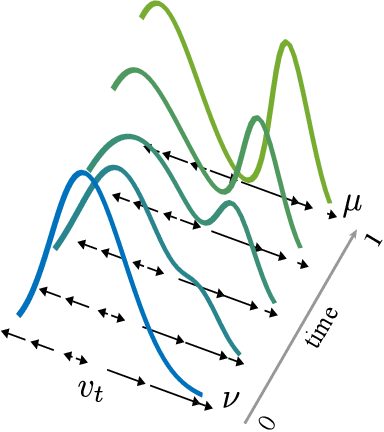
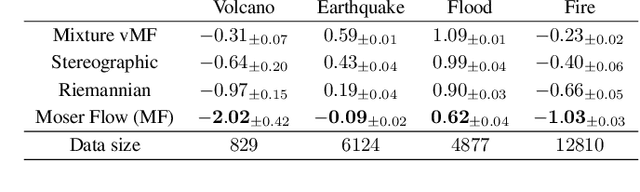
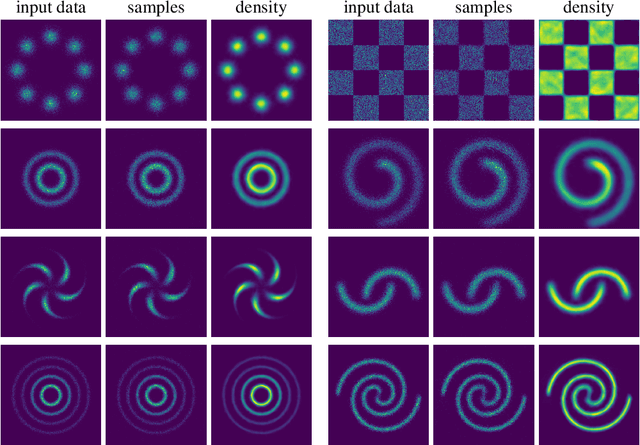
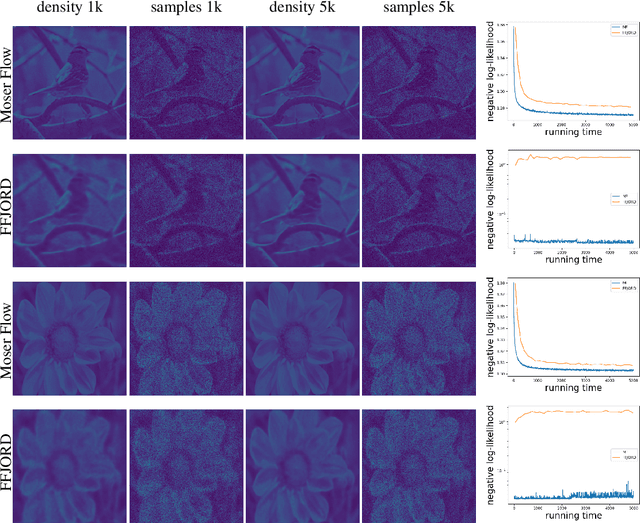
We are interested in learning generative models for complex geometries described via manifolds, such as spheres, tori, and other implicit surfaces. Current extensions of existing (Euclidean) generative models are restricted to specific geometries and typically suffer from high computational costs. We introduce Moser Flow (MF), a new class of generative models within the family of continuous normalizing flows (CNF). MF also produces a CNF via a solution to the change-of-variable formula, however differently from other CNF methods, its model (learned) density is parameterized as the source (prior) density minus the divergence of a neural network (NN). The divergence is a local, linear differential operator, easy to approximate and calculate on manifolds. Therefore, unlike other CNFs, MF does not require invoking or backpropagating through an ODE solver during training. Furthermore, representing the model density explicitly as the divergence of a NN rather than as a solution of an ODE facilitates learning high fidelity densities. Theoretically, we prove that MF constitutes a universal density approximator under suitable assumptions. Empirically, we demonstrate for the first time the use of flow models for sampling from general curved surfaces and achieve significant improvements in density estimation, sample quality, and training complexity over existing CNFs on challenging synthetic geometries and real-world benchmarks from the earth and climate sciences.

Volume Rendering of Neural Implicit Surfaces

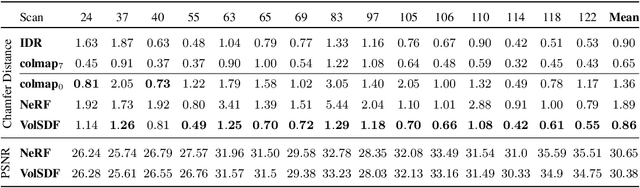
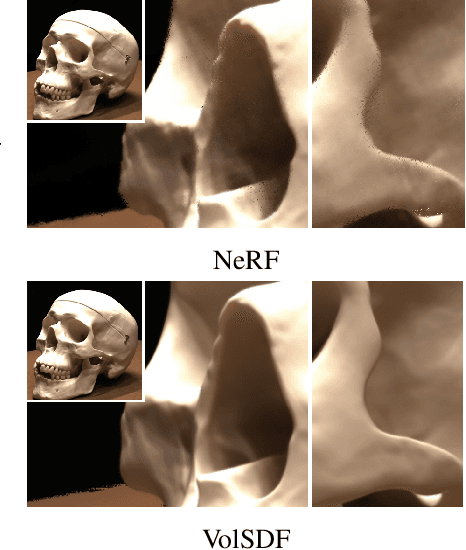
Neural volume rendering became increasingly popular recently due to its success in synthesizing novel views of a scene from a sparse set of input images. So far, the geometry learned by neural volume rendering techniques was modeled using a generic density function. Furthermore, the geometry itself was extracted using an arbitrary level set of the density function leading to a noisy, often low fidelity reconstruction. The goal of this paper is to improve geometry representation and reconstruction in neural volume rendering. We achieve that by modeling the volume density as a function of the geometry. This is in contrast to previous work modeling the geometry as a function of the volume density. In more detail, we define the volume density function as Laplace's cumulative distribution function (CDF) applied to a signed distance function (SDF) representation. This simple density representation has three benefits: (i) it provides a useful inductive bias to the geometry learned in the neural volume rendering process; (ii) it facilitates a bound on the opacity approximation error, leading to an accurate sampling of the viewing ray. Accurate sampling is important to provide a precise coupling of geometry and radiance; and (iii) it allows efficient unsupervised disentanglement of shape and appearance in volume rendering. Applying this new density representation to challenging scene multiview datasets produced high quality geometry reconstructions, outperforming relevant baselines. Furthermore, switching shape and appearance between scenes is possible due to the disentanglement of the two.

Riemannian Convex Potential Maps

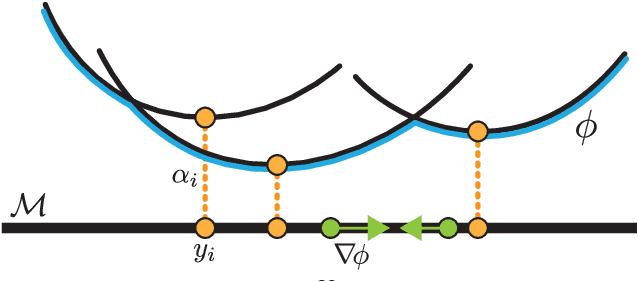
Modeling distributions on Riemannian manifolds is a crucial component in understanding non-Euclidean data that arises, e.g., in physics and geology. The budding approaches in this space are limited by representational and computational tradeoffs. We propose and study a class of flows that uses convex potentials from Riemannian optimal transport. These are universal and can model distributions on any compact Riemannian manifold without requiring domain knowledge of the manifold to be integrated into the architecture. We demonstrate that these flows can model standard distributions on spheres, and tori, on synthetic and geological data. Our source code is freely available online at http://github.com/facebookresearch/rcpm

Phase Transitions, Distance Functions, and Implicit Neural Representations

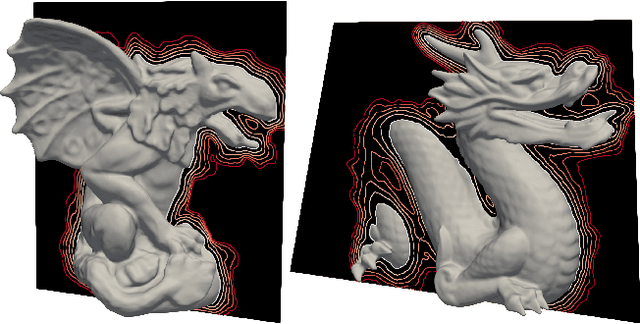
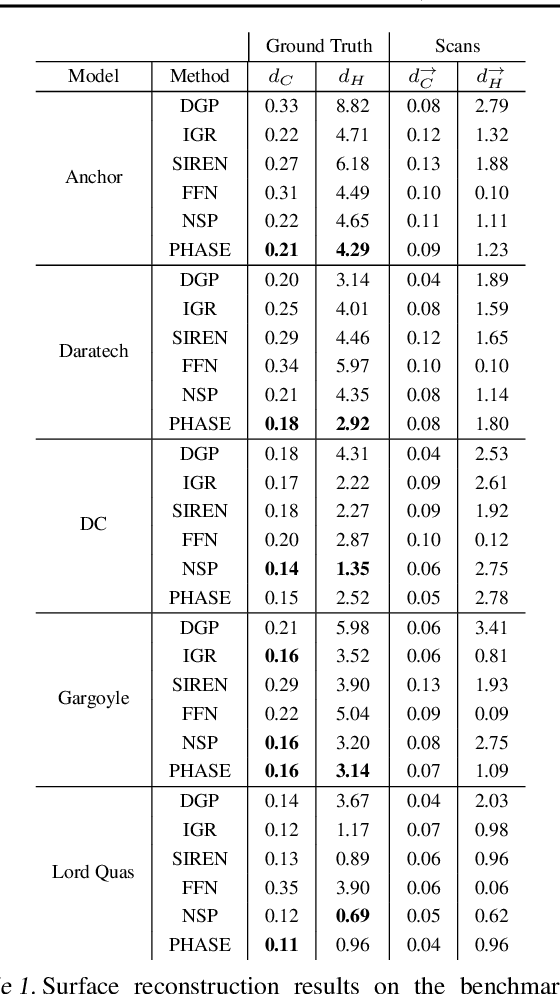
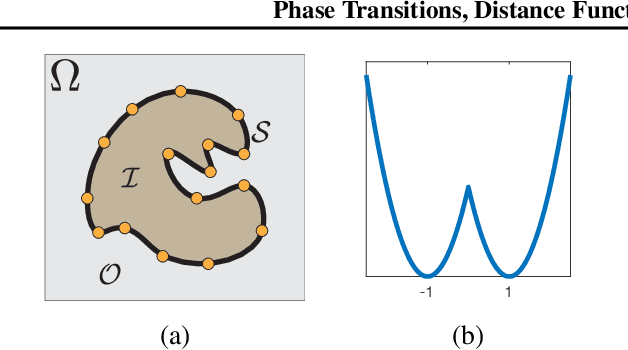
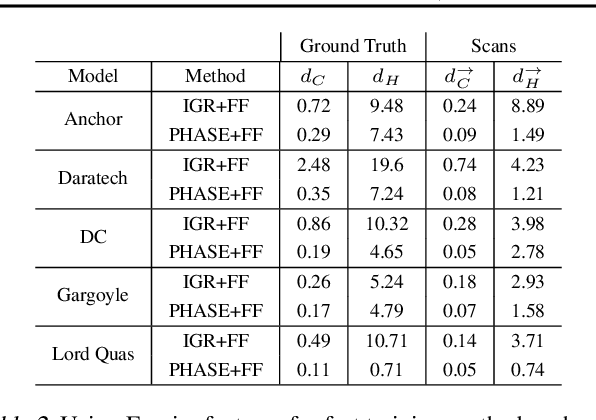
Representing surfaces as zero level sets of neural networks recently emerged as a powerful modeling paradigm, named Implicit Neural Representations (INRs), serving numerous downstream applications in geometric deep learning and 3D vision. Training INRs previously required choosing between occupancy and distance function representation and different losses with unknown limit behavior and/or bias. In this paper we draw inspiration from the theory of phase transitions of fluids and suggest a loss for training INRs that learns a density function that converges to a proper occupancy function, while its log transform converges to a distance function. Furthermore, we analyze the limit minimizer of this loss showing it satisfies the reconstruction constraints and has minimal surface perimeter, a desirable inductive bias for surface reconstruction. Training INRs with this new loss leads to state-of-the-art reconstructions on a standard benchmark.