SAS-Bench: A Fine-Grained Benchmark for Evaluating Short Answer Scoring with Large Language Models

Subjective Answer Grading (SAG) plays a crucial role in education, standardized testing, and automated assessment systems, particularly for evaluating short-form responses in Short Answer Scoring (SAS). However, existing approaches often produce coarse-grained scores and lack detailed reasoning. Although large language models (LLMs) have demonstrated potential as zero-shot evaluators, they remain susceptible to bias, inconsistencies with human judgment, and limited transparency in scoring decisions. To overcome these limitations, we introduce SAS-Bench, a benchmark specifically designed for LLM-based SAS tasks. SAS-Bench provides fine-grained, step-wise scoring, expert-annotated error categories, and a diverse range of question types derived from real-world subject-specific exams. This benchmark facilitates detailed evaluation of model reasoning processes and explainability. We also release an open-source dataset containing 1,030 questions and 4,109 student responses, each annotated by domain experts. Furthermore, we conduct comprehensive experiments with various LLMs, identifying major challenges in scoring science-related questions and highlighting the effectiveness of few-shot prompting in improving scoring accuracy. Our work offers valuable insights into the development of more robust, fair, and educationally meaningful LLM-based evaluation systems.

Multi-mode Tensor Train Factorization with Spatial-spectral Regularization for Remote Sensing Images Recovery

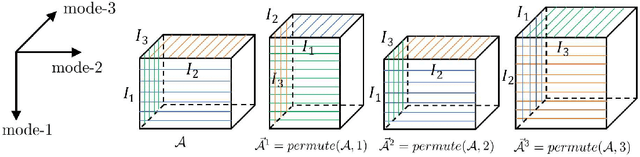
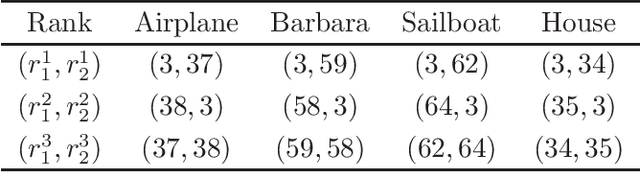
Tensor train (TT) factorization and corresponding TT rank, which can well express the low-rankness and mode correlations of higher-order tensors, have attracted much attention in recent years. However, TT factorization based methods are generally not sufficient to characterize low-rankness along each mode of third-order tensor. Inspired by this, we generalize the tensor train factorization to the mode-k tensor train factorization and introduce a corresponding multi-mode tensor train (MTT) rank. Then, we proposed a novel low-MTT-rank tensor completion model via multi-mode TT factorization and spatial-spectral smoothness regularization. To tackle the proposed model, we develop an efficient proximal alternating minimization (PAM) algorithm. Extensive numerical experiment results on visual data demonstrate that the proposed MTTD3R method outperforms compared methods in terms of visual and quantitative measures.

A DCT-based Tensor Completion Approach for Recovering Color Images and Videos from Highly Undersampled Data

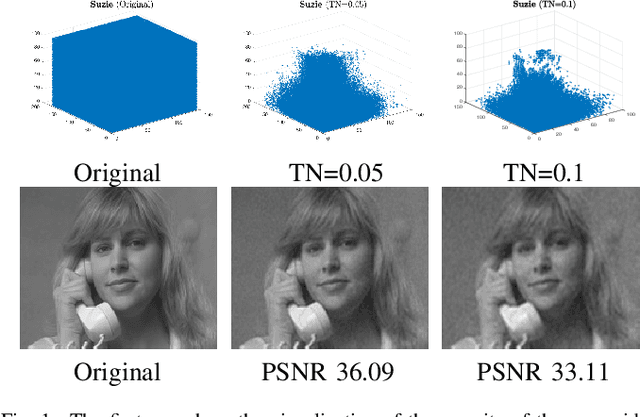
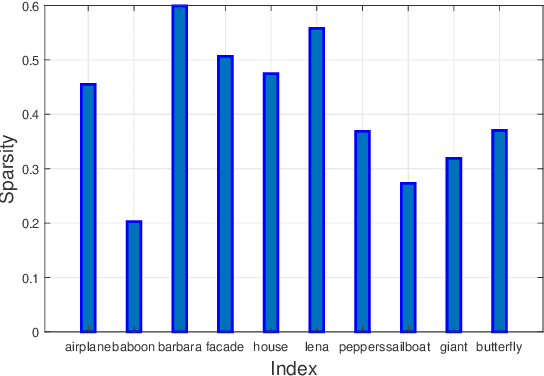
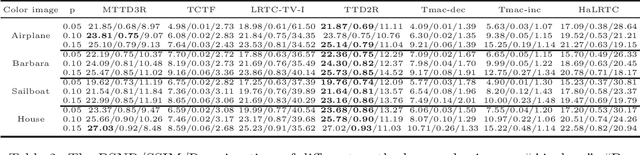
Recovering color images and videos from highly undersampled data is a fundamental and challenging task in face recognition and computer vision. By the multi-dimensional nature of color images and videos, in this paper, we propose a novel tensor completion approach, which is able to efficiently explore the sparsity of tensor data under the discrete cosine transform (DCT). Specifically, we introduce two DCT-based tensor completion models as well as two implementable algorithms for their solutions. The first one is a DCT-based weighted nuclear norm minimization model. The second one is called DCT-based $p$-shrinking tensor completion model, which is a nonconvex model utilizing $p$-shrinkage mapping for promoting the low-rankness of data. Moreover, we accordingly propose two implementable augmented Lagrangian-based algorithms for solving the underlying optimization models. A series of numerical experiments including color and MRI image inpainting and video data recovery demonstrate that our proposed approach performs better than many existing state-of-the-art tensor completion methods, especially for the case when the ratio of missing data is high.

Low-Rank and Sparse Enhanced Tucker Decomposition for Tensor Completion

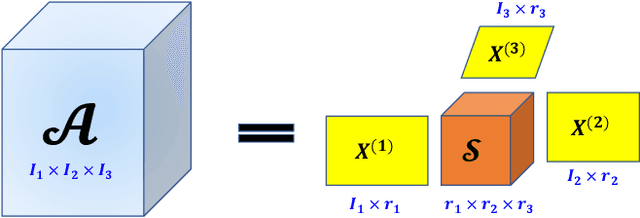
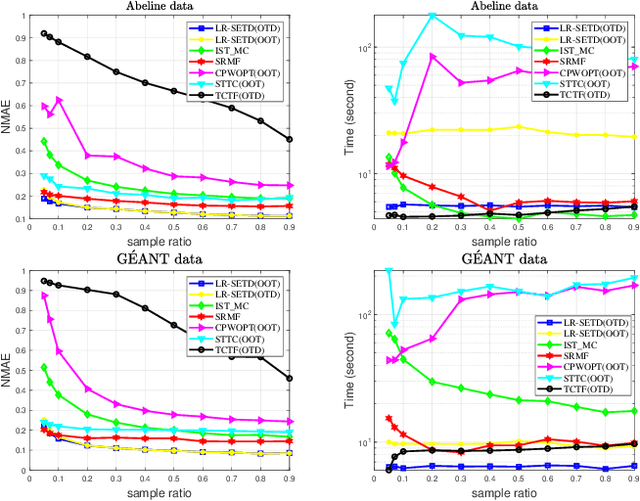
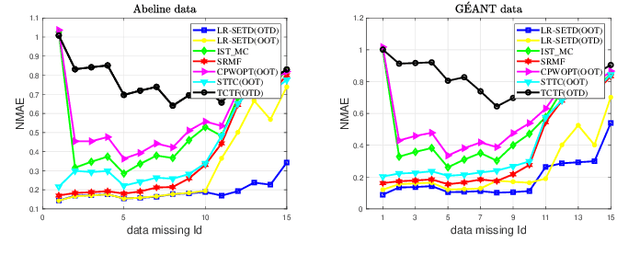
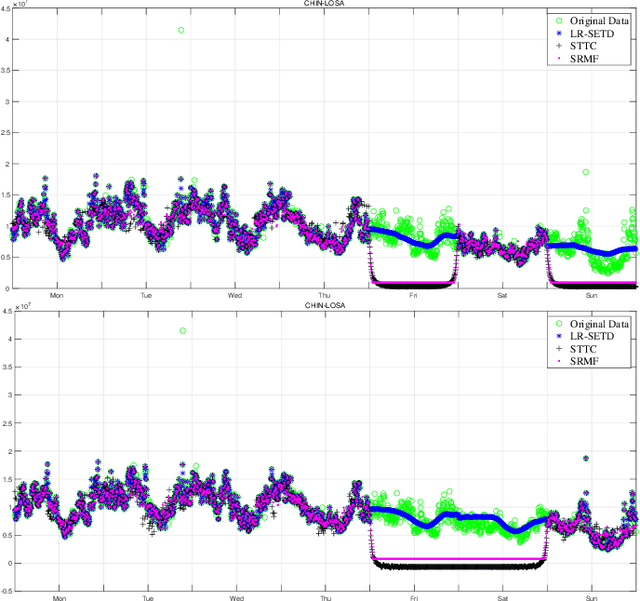
Tensor completion refers to the task of estimating the missing data from an incomplete measurement or observation, which is a core problem frequently arising from the areas of big data analysis, computer vision, and network engineering. Due to the multidimensional nature of high-order tensors, the matrix approaches, e.g., matrix factorization and direct matricization of tensors, are often not ideal for tensor completion and recovery. Exploiting the potential periodicity and inherent correlation properties appeared in real-world tensor data, in this paper, we shall incorporate the low-rank and sparse regularization technique to enhance Tucker decomposition for tensor completion. A series of computational experiments on real-world datasets, including internet traffic data, color images, and face recognition, show that our model performs better than many existing state-of-the-art matricization and tensorization approaches in terms of achieving higher recovery accuracy.