Multi-period Learning for Financial Time Series Forecasting

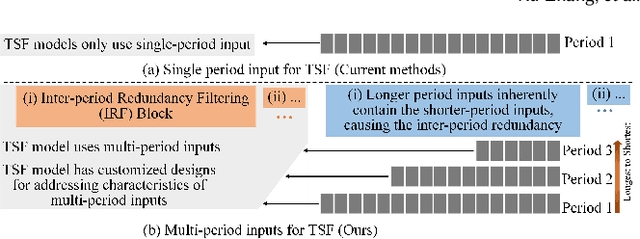
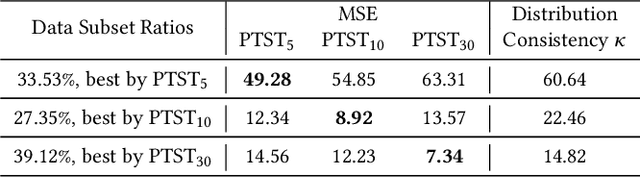
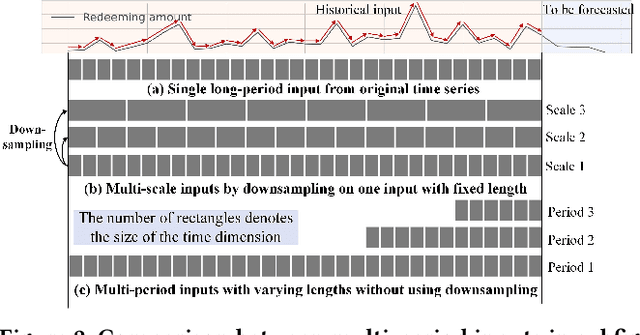
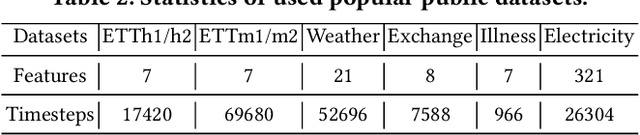
Time series forecasting is important in finance domain. Financial time series (TS) patterns are influenced by both short-term public opinions and medium-/long-term policy and market trends. Hence, processing multi-period inputs becomes crucial for accurate financial time series forecasting (TSF). However, current TSF models either use only single-period input, or lack customized designs for addressing multi-period characteristics. In this paper, we propose a Multi-period Learning Framework (MLF) to enhance financial TSF performance. MLF considers both TSF's accuracy and efficiency requirements. Specifically, we design three new modules to better integrate the multi-period inputs for improving accuracy: (i) Inter-period Redundancy Filtering (IRF), that removes the information redundancy between periods for accurate self-attention modeling, (ii) Learnable Weighted-average Integration (LWI), that effectively integrates multi-period forecasts, (iii) Multi-period self-Adaptive Patching (MAP), that mitigates the bias towards certain periods by setting the same number of patches across all periods. Furthermore, we propose a Patch Squeeze module to reduce the number of patches in self-attention modeling for maximized efficiency. MLF incorporates multiple inputs with varying lengths (periods) to achieve better accuracy and reduces the costs of selecting input lengths during training. The codes and datasets are available at https://github.com/Meteor-Stars/MLF.

A Unified Kernel for Neural Network Learning

Past decades have witnessed a great interest in the distinction and connection between neural network learning and kernel learning. Recent advancements have made theoretical progress in connecting infinite-wide neural networks and Gaussian processes. Two predominant approaches have emerged: the Neural Network Gaussian Process (NNGP) and the Neural Tangent Kernel (NTK). The former, rooted in Bayesian inference, represents a zero-order kernel, while the latter, grounded in the tangent space of gradient descents, is a first-order kernel. In this paper, we present the Unified Neural Kernel (UNK), which characterizes the learning dynamics of neural networks with gradient descents and parameter initialization. The proposed UNK kernel maintains the limiting properties of both NNGP and NTK, exhibiting behaviors akin to NTK with a finite learning step and converging to NNGP as the learning step approaches infinity. Besides, we also theoretically characterize the uniform tightness and learning convergence of the UNK kernel, providing comprehensive insights into this unified kernel. Experimental results underscore the effectiveness of our proposed method.