Accelerating RL for LLM Reasoning with Optimal Advantage Regression

Reinforcement learning (RL) has emerged as a powerful tool for fine-tuning large language models (LLMs) to improve complex reasoning abilities. However, state-of-the-art policy optimization methods often suffer from high computational overhead and memory consumption, primarily due to the need for multiple generations per prompt and the reliance on critic networks or advantage estimates of the current policy. In this paper, we propose $A$*-PO, a novel two-stage policy optimization framework that directly approximates the optimal advantage function and enables efficient training of LLMs for reasoning tasks. In the first stage, we leverage offline sampling from a reference policy to estimate the optimal value function $V$*, eliminating the need for costly online value estimation. In the second stage, we perform on-policy updates using a simple least-squares regression loss with only a single generation per prompt. Theoretically, we establish performance guarantees and prove that the KL-regularized RL objective can be optimized without requiring complex exploration strategies. Empirically, $A$*-PO achieves competitive performance across a wide range of mathematical reasoning benchmarks, while reducing training time by up to 2$\times$ and peak memory usage by over 30% compared to PPO, GRPO, and REBEL. Implementation of $A$*-PO can be found at https://github.com/ZhaolinGao/A-PO.

State-free Reinforcement Learning

In this work, we study the \textit{state-free RL} problem, where the algorithm does not have the states information before interacting with the environment. Specifically, denote the reachable state set by ${S}^\Pi := \{ s|\max_{\pi\in \Pi}q^{P, \pi}(s)>0 \}$, we design an algorithm which requires no information on the state space $S$ while having a regret that is completely independent of ${S}$ and only depend on ${S}^\Pi$. We view this as a concrete first step towards \textit{parameter-free RL}, with the goal of designing RL algorithms that require no hyper-parameter tuning.

Scale-free Adversarial Reinforcement Learning

This paper initiates the study of scale-free learning in Markov Decision Processes (MDPs), where the scale of rewards/losses is unknown to the learner. We design a generic algorithmic framework, \underline{S}cale \underline{C}lipping \underline{B}ound (\texttt{SCB}), and instantiate this framework in both the adversarial Multi-armed Bandit (MAB) setting and the adversarial MDP setting. Through this framework, we achieve the first minimax optimal expected regret bound and the first high-probability regret bound in scale-free adversarial MABs, resolving an open problem raised in \cite{hadiji2023adaptation}. On adversarial MDPs, our framework also give birth to the first scale-free RL algorithm with a $\tilde{\mathcal{O}}(\sqrt{T})$ high-probability regret guarantee.

Learning Adversarial Low-rank Markov Decision Processes with Unknown Transition and Full-information Feedback

In this work, we study the low-rank MDPs with adversarially changed losses in the full-information feedback setting. In particular, the unknown transition probability kernel admits a low-rank matrix decomposition \citep{REPUCB22}, and the loss functions may change adversarially but are revealed to the learner at the end of each episode. We propose a policy optimization-based algorithm POLO, and we prove that it attains the $\widetilde{O}(K^{\frac{5}{6}}A^{\frac{1}{2}}d\ln(1+M)/(1-\gamma)^2)$ regret guarantee, where $d$ is rank of the transition kernel (and hence the dimension of the unknown representations), $A$ is the cardinality of the action space, $M$ is the cardinality of the model class, and $\gamma$ is the discounted factor. Notably, our algorithm is oracle-efficient and has a regret guarantee with no dependence on the size of potentially arbitrarily large state space. Furthermore, we also prove an $\Omega(\frac{\gamma^2}{1-\gamma} \sqrt{d A K})$ regret lower bound for this problem, showing that low-rank MDPs are statistically more difficult to learn than linear MDPs in the regret minimization setting. To the best of our knowledge, we present the first algorithm that interleaves representation learning, exploration, and exploitation to achieve the sublinear regret guarantee for RL with nonlinear function approximation and adversarial losses.

Federated Multi-Level Optimization over Decentralized Networks

Multi-level optimization has gained increasing attention in recent years, as it provides a powerful framework for solving complex optimization problems that arise in many fields, such as meta-learning, multi-player games, reinforcement learning, and nested composition optimization. In this paper, we study the problem of distributed multi-level optimization over a network, where agents can only communicate with their immediate neighbors. This setting is motivated by the need for distributed optimization in large-scale systems, where centralized optimization may not be practical or feasible. To address this problem, we propose a novel gossip-based distributed multi-level optimization algorithm that enables networked agents to solve optimization problems at different levels in a single timescale and share information through network propagation. Our algorithm achieves optimal sample complexity, scaling linearly with the network size, and demonstrates state-of-the-art performance on various applications, including hyper-parameter tuning, decentralized reinforcement learning, and risk-averse optimization.

Improved Algorithms for Adversarial Bandits with Unbounded Losses

We consider the Adversarial Multi-Armed Bandits (MAB) problem with unbounded losses, where the algorithms have no prior knowledge on the sizes of the losses. We present UMAB-NN and UMAB-G, two algorithms for non-negative and general unbounded loss respectively. For non-negative unbounded loss, UMAB-NN achieves the first adaptive and scale free regret bound without uniform exploration. Built up on that, we further develop UMAB-G that can learn from arbitrary unbounded loss. Our analysis reveals the asymmetry between positive and negative losses in the MAB problem and provide additional insights. We also accompany our theoretical findings with extensive empirical evaluations, showing that our algorithms consistently out-performs all existing algorithms that handles unbounded losses.

Provably Efficient Representation Learning with Tractable Planning in Low-Rank POMDP

In this paper, we study representation learning in partially observable Markov Decision Processes (POMDPs), where the agent learns a decoder function that maps a series of high-dimensional raw observations to a compact representation and uses it for more efficient exploration and planning. We focus our attention on the sub-classes of \textit{$\gamma$-observable} and \textit{decodable POMDPs}, for which it has been shown that statistically tractable learning is possible, but there has not been any computationally efficient algorithm. We first present an algorithm for decodable POMDPs that combines maximum likelihood estimation (MLE) and optimism in the face of uncertainty (OFU) to perform representation learning and achieve efficient sample complexity, while only calling supervised learning computational oracles. We then show how to adapt this algorithm to also work in the broader class of $\gamma$-observable POMDPs.

Provable Defense against Backdoor Policies in Reinforcement Learning

We propose a provable defense mechanism against backdoor policies in reinforcement learning under subspace trigger assumption. A backdoor policy is a security threat where an adversary publishes a seemingly well-behaved policy which in fact allows hidden triggers. During deployment, the adversary can modify observed states in a particular way to trigger unexpected actions and harm the agent. We assume the agent does not have the resources to re-train a good policy. Instead, our defense mechanism sanitizes the backdoor policy by projecting observed states to a 'safe subspace', estimated from a small number of interactions with a clean (non-triggered) environment. Our sanitized policy achieves $\epsilon$ approximate optimality in the presence of triggers, provided the number of clean interactions is $O\left(\frac{D}{(1-\gamma)^4 \epsilon^2}\right)$ where $\gamma$ is the discounting factor and $D$ is the dimension of state space. Empirically, we show that our sanitization defense performs well on two Atari game environments.

Representation Learning for General-sum Low-rank Markov Games

We study multi-agent general-sum Markov games with nonlinear function approximation. We focus on low-rank Markov games whose transition matrix admits a hidden low-rank structure on top of an unknown non-linear representation. The goal is to design an algorithm that (1) finds an $\varepsilon$-equilibrium policy sample efficiently without prior knowledge of the environment or the representation, and (2) permits a deep-learning friendly implementation. We leverage representation learning and present a model-based and a model-free approach to construct an effective representation from the collected data. For both approaches, the algorithm achieves a sample complexity of poly$(H,d,A,1/\varepsilon)$, where $H$ is the game horizon, $d$ is the dimension of the feature vector, $A$ is the size of the joint action space and $\varepsilon$ is the optimality gap. When the number of players is large, the above sample complexity can scale exponentially with the number of players in the worst case. To address this challenge, we consider Markov games with a factorized transition structure and present an algorithm that escapes such exponential scaling. To our best knowledge, this is the first sample-efficient algorithm for multi-agent general-sum Markov games that incorporates (non-linear) function approximation. We accompany our theoretical result with a neural network-based implementation of our algorithm and evaluate it against the widely used deep RL baseline, DQN with fictitious play.

Provably Efficient Reinforcement Learning for Online Adaptive Influence Maximization

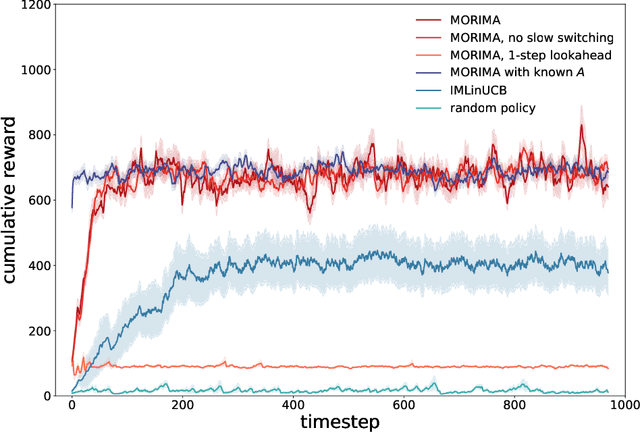
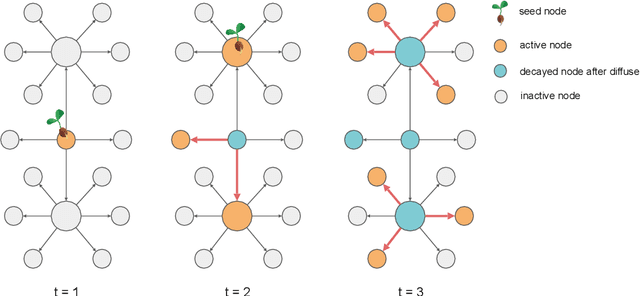
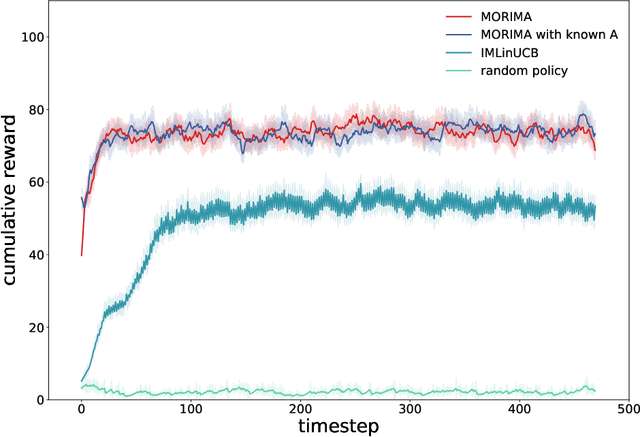
Online influence maximization aims to maximize the influence spread of a content in a social network with unknown network model by selecting a few seed nodes. Recent studies followed a non-adaptive setting, where the seed nodes are selected before the start of the diffusion process and network parameters are updated when the diffusion stops. We consider an adaptive version of content-dependent online influence maximization problem where the seed nodes are sequentially activated based on real-time feedback. In this paper, we formulate the problem as an infinite-horizon discounted MDP under a linear diffusion process and present a model-based reinforcement learning solution. Our algorithm maintains a network model estimate and selects seed users adaptively, exploring the social network while improving the optimal policy optimistically. We establish $\widetilde O(\sqrt{T})$ regret bound for our algorithm. Empirical evaluations on synthetic network demonstrate the efficiency of our algorithm.