Price of Safety in Linear Best Arm Identification

We introduce the safe best-arm identification framework with linear feedback, where the agent is subject to some stage-wise safety constraint that linearly depends on an unknown parameter vector. The agent must take actions in a conservative way so as to ensure that the safety constraint is not violated with high probability at each round. Ways of leveraging the linear structure for ensuring safety has been studied for regret minimization, but not for best-arm identification to the best our knowledge. We propose a gap-based algorithm that achieves meaningful sample complexity while ensuring the stage-wise safety. We show that we pay an extra term in the sample complexity due to the forced exploration phase incurred by the additional safety constraint. Experimental illustrations are provided to justify the design of our algorithm.

UCB Momentum Q-learning: Correcting the bias without forgetting

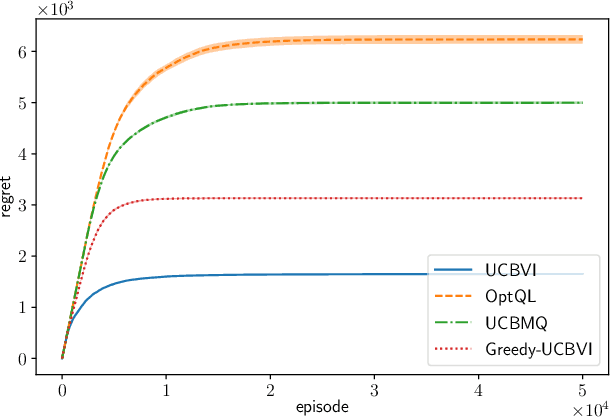
We propose UCBMQ, Upper Confidence Bound Momentum Q-learning, a new algorithm for reinforcement learning in tabular and possibly stage-dependent, episodic Markov decision process. UCBMQ is based on Q-learning where we add a momentum term and rely on the principle of optimism in face of uncertainty to deal with exploration. Our new technical ingredient of UCBMQ is the use of momentum to correct the bias that Q-learning suffers while, at the same time, limiting the impact it has on the second-order term of the regret. For UCBMQ , we are able to guarantee a regret of at most $O(\sqrt{H^3SAT}+ H^4 S A )$ where $H$ is the length of an episode, $S$ the number of states, $A$ the number of actions, $T$ the number of episodes and ignoring terms in poly$log(SAHT)$. Notably, UCBMQ is the first algorithm that simultaneously matches the lower bound of $\Omega(\sqrt{H^3SAT})$ for large enough $T$ and has a second-order term (with respect to the horizon $T$) that scales only linearly with the number of states $S$.

Stochastic Bandits with Vector Losses: Minimizing $\ell^\infty$-Norm of Relative Losses

Multi-armed bandits are widely applied in scenarios like recommender systems, for which the goal is to maximize the click rate. However, more factors should be considered, e.g., user stickiness, user growth rate, user experience assessment, etc. In this paper, we model this situation as a problem of $K$-armed bandit with multiple losses. We define relative loss vector of an arm where the $i$-th entry compares the arm and the optimal arm with respect to the $i$-th loss. We study two goals: (a) finding the arm with the minimum $\ell^\infty$-norm of relative losses with a given confidence level (which refers to fixed-confidence best-arm identification); (b) minimizing the $\ell^\infty$-norm of cumulative relative losses (which refers to regret minimization). For goal (a), we derive a problem-dependent sample complexity lower bound and discuss how to achieve matching algorithms. For goal (b), we provide a regret lower bound of $\Omega(T^{2/3})$ and provide a matching algorithm.

Gamification of Pure Exploration for Linear Bandits

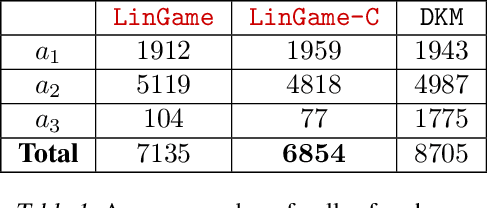
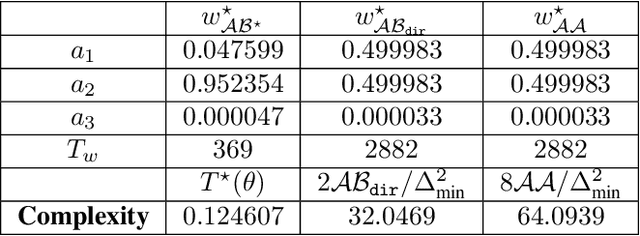
We investigate an active pure-exploration setting, that includes best-arm identification, in the context of linear stochastic bandits. While asymptotically optimal algorithms exist for standard multi-arm bandits, the existence of such algorithms for the best-arm identification in linear bandits has been elusive despite several attempts to address it. First, we provide a thorough comparison and new insight over different notions of optimality in the linear case, including G-optimality, transductive optimality from optimal experimental design and asymptotic optimality. Second, we design the first asymptotically optimal algorithm for fixed-confidence pure exploration in linear bandits. As a consequence, our algorithm naturally bypasses the pitfall caused by a simple but difficult instance, that most prior algorithms had to be engineered to deal with explicitly. Finally, we avoid the need to fully solve an optimal design problem by providing an approach that entails an efficient implementation.

Fixed-Confidence Guarantees for Bayesian Best-Arm Identification

We investigate and provide new insights on the sampling rule called Top-Two Thompson Sampling (TTTS). In particular, we justify its use for fixed-confidence best-arm identification. We further propose a variant of TTTS called Top-Two Transportation Cost (T3C), which disposes of the computational burden of TTTS. As our main contribution, we provide the first sample complexity analysis of TTTS and T3C when coupled with a very natural Bayesian stopping rule, for bandits with Gaussian rewards, solving one of the open questions raised by Russo (2016). We also provide new posterior convergence results for TTTS under two models that are commonly used in practice: bandits with Gaussian and Bernoulli rewards and conjugate priors.