Best-Arm Identification in Unimodal Bandits

We study the fixed-confidence best-arm identification problem in unimodal bandits, in which the means of the arms increase with the index of the arm up to their maximum, then decrease. We derive two lower bounds on the stopping time of any algorithm. The instance-dependent lower bound suggests that due to the unimodal structure, only three arms contribute to the leading confidence-dependent cost. However, a worst-case lower bound shows that a linear dependence on the number of arms is unavoidable in the confidence-independent cost. We propose modifications of Track-and-Stop and a Top Two algorithm that leverage the unimodal structure. Both versions of Track-and-Stop are asymptotically optimal for one-parameter exponential families. The Top Two algorithm is asymptotically near-optimal for Gaussian distributions and we prove a non-asymptotic guarantee matching the worse-case lower bound. The algorithms can be implemented efficiently and we demonstrate their competitive empirical performance.

Optimal Multi-Fidelity Best-Arm Identification

In bandit best-arm identification, an algorithm is tasked with finding the arm with highest mean reward with a specified accuracy as fast as possible. We study multi-fidelity best-arm identification, in which the algorithm can choose to sample an arm at a lower fidelity (less accurate mean estimate) for a lower cost. Several methods have been proposed for tackling this problem, but their optimality remain elusive, notably due to loose lower bounds on the total cost needed to identify the best arm. Our first contribution is a tight, instance-dependent lower bound on the cost complexity. The study of the optimization problem featured in the lower bound provides new insights to devise computationally efficient algorithms, and leads us to propose a gradient-based approach with asymptotically optimal cost complexity. We demonstrate the benefits of the new algorithm compared to existing methods in experiments. Our theoretical and empirical findings also shed light on an intriguing concept of optimal fidelity for each arm.

Finding good policies in average-reward Markov Decision Processes without prior knowledge

We revisit the identification of an $\varepsilon$-optimal policy in average-reward Markov Decision Processes (MDP). In such MDPs, two measures of complexity have appeared in the literature: the diameter, $D$, and the optimal bias span, $H$, which satisfy $H\leq D$. Prior work have studied the complexity of $\varepsilon$-optimal policy identification only when a generative model is available. In this case, it is known that there exists an MDP with $D \simeq H$ for which the sample complexity to output an $\varepsilon$-optimal policy is $\Omega(SAD/\varepsilon^2)$ where $S$ and $A$ are the sizes of the state and action spaces. Recently, an algorithm with a sample complexity of order $SAH/\varepsilon^2$ has been proposed, but it requires the knowledge of $H$. We first show that the sample complexity required to estimate $H$ is not bounded by any function of $S,A$ and $H$, ruling out the possibility to easily make the previous algorithm agnostic to $H$. By relying instead on a diameter estimation procedure, we propose the first algorithm for $(\varepsilon,\delta)$-PAC policy identification that does not need any form of prior knowledge on the MDP. Its sample complexity scales in $SAD/\varepsilon^2$ in the regime of small $\varepsilon$, which is near-optimal. In the online setting, our first contribution is a lower bound which implies that a sample complexity polynomial in $H$ cannot be achieved in this setting. Then, we propose an online algorithm with a sample complexity in $SAD^2/\varepsilon^2$, as well as a novel approach based on a data-dependent stopping rule that we believe is promising to further reduce this bound.

An $\varepsilon$-Best-Arm Identification Algorithm for Fixed-Confidence and Beyond

We propose EB-TC$\varepsilon$, a novel sampling rule for $\varepsilon$-best arm identification in stochastic bandits. It is the first instance of Top Two algorithm analyzed for approximate best arm identification. EB-TC$\varepsilon$ is an *anytime* sampling rule that can therefore be employed without modification for fixed confidence or fixed budget identification (without prior knowledge of the budget). We provide three types of theoretical guarantees for EB-TC$\varepsilon$. First, we prove bounds on its expected sample complexity in the fixed confidence setting, notably showing its asymptotic optimality in combination with an adaptive tuning of its exploration parameter. We complement these findings with upper bounds on its probability of error at any time and for any error parameter, which further yield upper bounds on its simple regret at any time. Finally, we show through numerical simulations that EB-TC$\varepsilon$ performs favorably compared to existing algorithms, in different settings.

On the Existence of a Complexity in Fixed Budget Bandit Identification

In fixed budget bandit identification, an algorithm sequentially observes samples from several distributions up to a given final time. It then answers a query about the set of distributions. A good algorithm will have a small probability of error. While that probability decreases exponentially with the final time, the best attainable rate is not known precisely for most identification tasks. We show that if a fixed budget task admits a complexity, defined as a lower bound on the probability of error which is attained by a single algorithm on all bandit problems, then that complexity is determined by the best non-adaptive sampling procedure for that problem. We show that there is no such complexity for several fixed budget identification tasks including Bernoulli best arm identification with two arms: there is no single algorithm that attains everywhere the best possible rate.

Non-Asymptotic Analysis of a UCB-based Top Two Algorithm

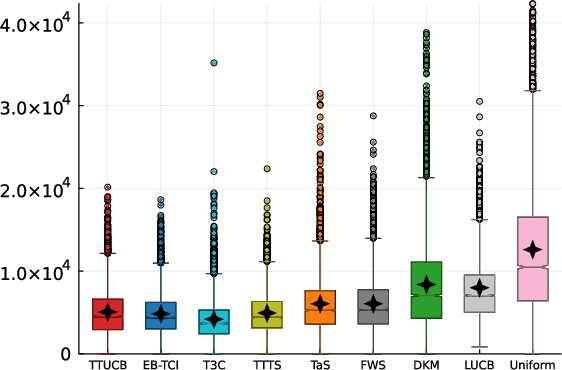
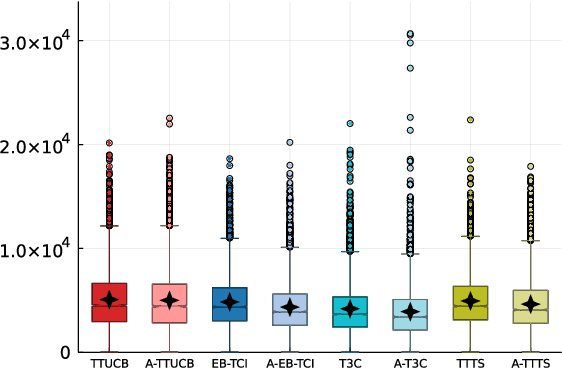
A Top Two sampling rule for bandit identification is a method which selects the next arm to sample from among two candidate arms, a leader and a challenger. Due to their simplicity and good empirical performance, they have received increased attention in recent years. For fixed-confidence best arm identification, theoretical guarantees for Top Two methods have only been obtained in the asymptotic regime, when the error level vanishes. We derive the first non-asymptotic upper bound on the expected sample complexity of a Top Two algorithm holding for any error level. Our analysis highlights sufficient properties for a regret minimization algorithm to be used as leader. They are satisfied by the UCB algorithm and our proposed UCB-based Top Two algorithm enjoys simultaneously non-asymptotic guarantees and competitive empirical performance.

Dealing with Unknown Variances in Best-Arm Identification

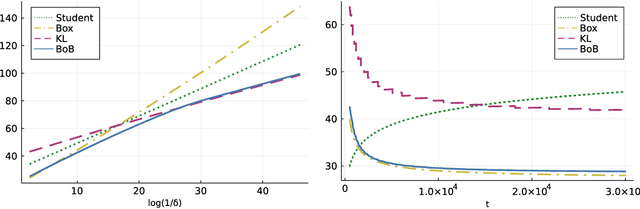
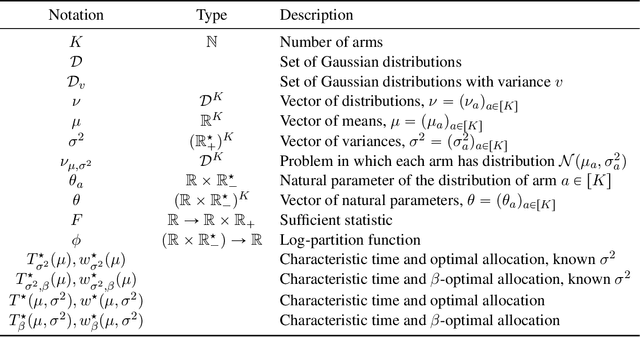
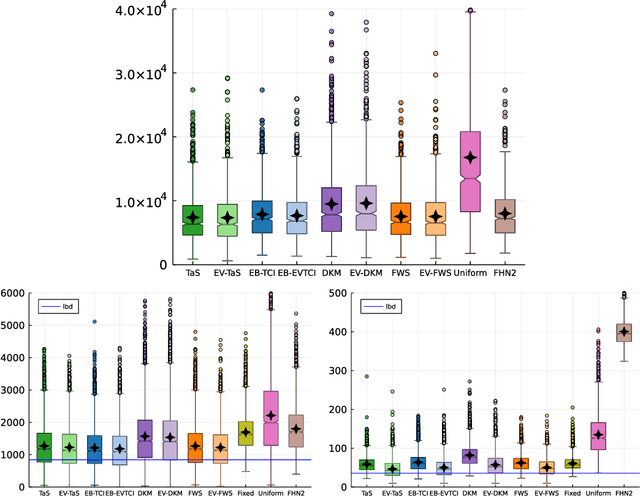
The problem of identifying the best arm among a collection of items having Gaussian rewards distribution is well understood when the variances are known. Despite its practical relevance for many applications, few works studied it for unknown variances. In this paper we introduce and analyze two approaches to deal with unknown variances, either by plugging in the empirical variance or by adapting the transportation costs. In order to calibrate our two stopping rules, we derive new time-uniform concentration inequalities, which are of independent interest. Then, we illustrate the theoretical and empirical performances of our two sampling rule wrappers on Track-and-Stop and on a Top Two algorithm. Moreover, by quantifying the impact on the sample complexity of not knowing the variances, we reveal that it is rather small.

Top Two Algorithms Revisited

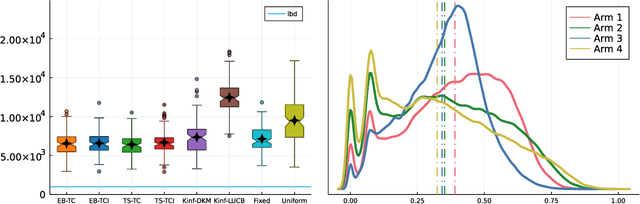
Top Two algorithms arose as an adaptation of Thompson sampling to best arm identification in multi-armed bandit models (Russo, 2016), for parametric families of arms. They select the next arm to sample from by randomizing among two candidate arms, a leader and a challenger. Despite their good empirical performance, theoretical guarantees for fixed-confidence best arm identification have only been obtained when the arms are Gaussian with known variances. In this paper, we provide a general analysis of Top Two methods, which identifies desirable properties of the leader, the challenger, and the (possibly non-parametric) distributions of the arms. As a result, we obtain theoretically supported Top Two algorithms for best arm identification with bounded distributions. Our proof method demonstrates in particular that the sampling step used to select the leader inherited from Thompson sampling can be replaced by other choices, like selecting the empirical best arm.

Choosing Answers in $\varepsilon$-Best-Answer Identification for Linear Bandits

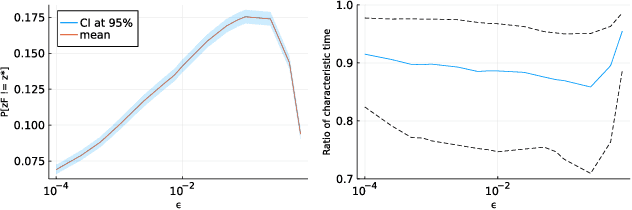
In pure-exploration problems, information is gathered sequentially to answer a question on the stochastic environment. While best-arm identification for linear bandits has been extensively studied in recent years, few works have been dedicated to identifying one arm that is $\varepsilon$-close to the best one (and not exactly the best one). In this problem with several correct answers, an identification algorithm should focus on one candidate among those answers and verify that it is correct. We demonstrate that picking the answer with highest mean does not allow an algorithm to reach asymptotic optimality in terms of expected sample complexity. Instead, a \textit{furthest answer} should be identified. Using that insight to choose the candidate answer carefully, we develop a simple procedure to adapt best-arm identification algorithms to tackle $\varepsilon$-best-answer identification in transductive linear stochastic bandits. Finally, we propose an asymptotically optimal algorithm for this setting, which is shown to achieve competitive empirical performance against existing modified best-arm identification algorithms.

On Elimination Strategies for Bandit Fixed-Confidence Identification

Elimination algorithms for bandit identification, which prune the plausible correct answers sequentially until only one remains, are computationally convenient since they reduce the problem size over time. However, existing elimination strategies are often not fully adaptive (they update their sampling rule infrequently) and are not easy to extend to combinatorial settings, where the set of answers is exponentially large in the problem dimension. On the other hand, most existing fully-adaptive strategies to tackle general identification problems are computationally demanding since they repeatedly test the correctness of every answer, without ever reducing the problem size. We show that adaptive methods can be modified to use elimination in both their stopping and sampling rules, hence obtaining the best of these two worlds: the algorithms (1) remain fully adaptive, (2) suffer a sample complexity that is never worse of their non-elimination counterpart, and (3) provably eliminate certain wrong answers early. We confirm these benefits experimentally, where elimination improves significantly the computational complexity of adaptive methods on common tasks like best-arm identification in linear bandits.