Probably Approximately Precision and Recall Learning

Precision and Recall are foundational metrics in machine learning where both accurate predictions and comprehensive coverage are essential, such as in recommender systems and multi-label learning. In these tasks, balancing precision (the proportion of relevant items among those predicted) and recall (the proportion of relevant items successfully predicted) is crucial. A key challenge is that one-sided feedback--where only positive examples are observed during training--is inherent in many practical problems. For instance, in recommender systems like YouTube, training data only consists of videos that a user has actively selected, while unselected items remain unseen. Despite this lack of negative feedback in training, avoiding undesirable recommendations at test time is essential. We introduce a PAC learning framework where each hypothesis is represented by a graph, with edges indicating positive interactions, such as between users and items. This framework subsumes the classical binary and multi-class PAC learning models as well as multi-label learning with partial feedback, where only a single random correct label per example is observed, rather than all correct labels. Our work uncovers a rich statistical and algorithmic landscape, with nuanced boundaries on what can and cannot be learned. Notably, classical methods like Empirical Risk Minimization fail in this setting, even for simple hypothesis classes with only two hypotheses. To address these challenges, we develop novel algorithms that learn exclusively from positive data, effectively minimizing both precision and recall losses. Specifically, in the realizable setting, we design algorithms that achieve optimal sample complexity guarantees. In the agnostic case, we show that it is impossible to achieve additive error guarantees--as is standard in PAC learning--and instead obtain meaningful multiplicative approximations.

Transformation-Invariant Learning and Theoretical Guarantees for OOD Generalization

Learning with identical train and test distributions has been extensively investigated both practically and theoretically. Much remains to be understood, however, in statistical learning under distribution shifts. This paper focuses on a distribution shift setting where train and test distributions can be related by classes of (data) transformation maps. We initiate a theoretical study for this framework, investigating learning scenarios where the target class of transformations is either known or unknown. We establish learning rules and algorithmic reductions to Empirical Risk Minimization (ERM), accompanied with learning guarantees. We obtain upper bounds on the sample complexity in terms of the VC dimension of the class composing predictors with transformations, which we show in many cases is not much larger than the VC dimension of the class of predictors. We highlight that the learning rules we derive offer a game-theoretic viewpoint on distribution shift: a learner searching for predictors and an adversary searching for transformation maps to respectively minimize and maximize the worst-case loss.

Trustworthy Machine Learning under Social and Adversarial Data Sources

Machine learning has witnessed remarkable breakthroughs in recent years. As machine learning permeates various aspects of daily life, individuals and organizations increasingly interact with these systems, exhibiting a wide range of social and adversarial behaviors. These behaviors may have a notable impact on the behavior and performance of machine learning systems. Specifically, during these interactions, data may be generated by strategic individuals, collected by self-interested data collectors, possibly poisoned by adversarial attackers, and used to create predictors, models, and policies satisfying multiple objectives. As a result, the machine learning systems' outputs might degrade, such as the susceptibility of deep neural networks to adversarial examples (Shafahi et al., 2018; Szegedy et al., 2013) and the diminished performance of classic algorithms in the presence of strategic individuals (Ahmadi et al., 2021). Addressing these challenges is imperative for the success of machine learning in societal settings.

Learnability Gaps of Strategic Classification

In contrast with standard classification tasks, strategic classification involves agents strategically modifying their features in an effort to receive favorable predictions. For instance, given a classifier determining loan approval based on credit scores, applicants may open or close their credit cards to fool the classifier. The learning goal is to find a classifier robust against strategic manipulations. Various settings, based on what and when information is known, have been explored in strategic classification. In this work, we focus on addressing a fundamental question: the learnability gaps between strategic classification and standard learning. We essentially show that any learnable class is also strategically learnable: we first consider a fully informative setting, where the manipulation structure (which is modeled by a manipulation graph $G^\star$) is known and during training time the learner has access to both the pre-manipulation data and post-manipulation data. We provide nearly tight sample complexity and regret bounds, offering significant improvements over prior results. Then, we relax the fully informative setting by introducing two natural types of uncertainty. First, following Ahmadi et al. (2023), we consider the setting in which the learner only has access to the post-manipulation data. We improve the results of Ahmadi et al. (2023) and close the gap between mistake upper bound and lower bound raised by them. Our second relaxation of the fully informative setting introduces uncertainty to the manipulation structure. That is, we assume that the manipulation graph is unknown but belongs to a known class of graphs. We provide nearly tight bounds on the learning complexity in various unknown manipulation graph settings. Notably, our algorithm in this setting is of independent interest and can be applied to other problems such as multi-label learning.

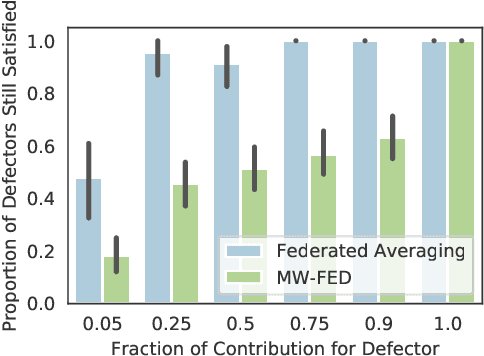
On the Effect of Defections in Federated Learning and How to Prevent Them

Federated learning is a machine learning protocol that enables a large population of agents to collaborate over multiple rounds to produce a single consensus model. There are several federated learning applications where agents may choose to defect permanently$-$essentially withdrawing from the collaboration$-$if they are content with their instantaneous model in that round. This work demonstrates the detrimental impact of such defections on the final model's robustness and ability to generalize. We also show that current federated optimization algorithms fail to disincentivize these harmful defections. We introduce a novel optimization algorithm with theoretical guarantees to prevent defections while ensuring asymptotic convergence to an effective solution for all participating agents. We also provide numerical experiments to corroborate our findings and demonstrate the effectiveness of our algorithm.

Incentivized Collaboration in Active Learning

In collaborative active learning, where multiple agents try to learn labels from a common hypothesis, we introduce an innovative framework for incentivized collaboration. Here, rational agents aim to obtain labels for their data sets while keeping label complexity at a minimum. We focus on designing (strict) individually rational (IR) collaboration protocols, ensuring that agents cannot reduce their expected label complexity by acting individually. We first show that given any optimal active learning algorithm, the collaboration protocol that runs the algorithm as is over the entire data is already IR. However, computing the optimal algorithm is NP-hard. We therefore provide collaboration protocols that achieve (strict) IR and are comparable with the best known tractable approximation algorithm in terms of label complexity.

Strategic Classification under Unknown Personalized Manipulation

We study the fundamental mistake bound and sample complexity in the strategic classification, where agents can strategically manipulate their feature vector up to an extent in order to be predicted as positive. For example, given a classifier determining college admission, student candidates may try to take easier classes to improve their GPA, retake SAT and change schools in an effort to fool the classifier. Ball manipulations are a widely studied class of manipulations in the literature, where agents can modify their feature vector within a bounded radius ball. Unlike most prior work, our work considers manipulations to be personalized, meaning that agents can have different levels of manipulation abilities (e.g., varying radii for ball manipulations), and unknown to the learner. We formalize the learning problem in an interaction model where the learner first deploys a classifier and the agent manipulates the feature vector within their manipulation set to game the deployed classifier. We investigate various scenarios in terms of the information available to the learner during the interaction, such as observing the original feature vector before or after deployment, observing the manipulated feature vector, or not seeing either the original or the manipulated feature vector. We begin by providing online mistake bounds and PAC sample complexity in these scenarios for ball manipulations. We also explore non-ball manipulations and show that, even in the simplest scenario where both the original and the manipulated feature vectors are revealed, the mistake bounds and sample complexity are lower bounded by $\Omega(|\mathcal{H}|)$ when the target function belongs to a known class $\mathcal{H}$.

Eliciting User Preferences for Personalized Multi-Objective Decision Making through Comparative Feedback

In classic reinforcement learning (RL) and decision making problems, policies are evaluated with respect to a scalar reward function, and all optimal policies are the same with regards to their expected return. However, many real-world problems involve balancing multiple, sometimes conflicting, objectives whose relative priority will vary according to the preferences of each user. Consequently, a policy that is optimal for one user might be sub-optimal for another. In this work, we propose a multi-objective decision making framework that accommodates different user preferences over objectives, where preferences are learned via policy comparisons. Our model consists of a Markov decision process with a vector-valued reward function, with each user having an unknown preference vector that expresses the relative importance of each objective. The goal is to efficiently compute a near-optimal policy for a given user. We consider two user feedback models. We first address the case where a user is provided with two policies and returns their preferred policy as feedback. We then move to a different user feedback model, where a user is instead provided with two small weighted sets of representative trajectories and selects the preferred one. In both cases, we suggest an algorithm that finds a nearly optimal policy for the user using a small number of comparison queries.

A Theory of PAC Learnability under Transformation Invariances

Transformation invariances are present in many real-world problems. For example, image classification is usually invariant to rotation and color transformation: a rotated car in a different color is still identified as a car. Data augmentation, which adds the transformed data into the training set and trains a model on the augmented data, is one commonly used technique to build these invariances into the learning process. However, it is unclear how data augmentation performs theoretically and what the optimal algorithm is in presence of transformation invariances. In this paper, we study PAC learnability under transformation invariances in three settings according to different levels of realizability: (i) A hypothesis fits the augmented data; (ii) A hypothesis fits only the original data and the transformed data lying in the support of the data distribution; (iii) Agnostic case. One interesting observation is that distinguishing between the original data and the transformed data is necessary to achieve optimal accuracy in setting (ii) and (iii), which implies that any algorithm not differentiating between the original and transformed data (including data augmentation) is not optimal. Furthermore, this type of algorithms can even "harm" the accuracy. In setting (i), although it is unnecessary to distinguish between the two data sets, data augmentation still does not perform optimally. Due to such a difference, we propose two combinatorial measures characterizing the optimal sample complexity in setting (i) and (ii)(iii) and provide the optimal algorithms.

One for One, or All for All: Equilibria and Optimality of Collaboration in Federated Learning

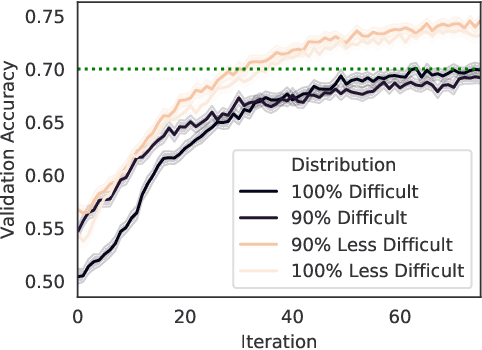
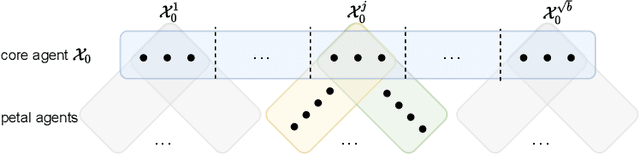
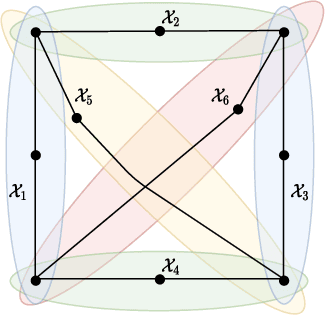
In recent years, federated learning has been embraced as an approach for bringing about collaboration across large populations of learning agents. However, little is known about how collaboration protocols should take agents' incentives into account when allocating individual resources for communal learning in order to maintain such collaborations. Inspired by game theoretic notions, this paper introduces a framework for incentive-aware learning and data sharing in federated learning. Our stable and envy-free equilibria capture notions of collaboration in the presence of agents interested in meeting their learning objectives while keeping their own sample collection burden low. For example, in an envy-free equilibrium, no agent would wish to swap their sampling burden with any other agent and in a stable equilibrium, no agent would wish to unilaterally reduce their sampling burden. In addition to formalizing this framework, our contributions include characterizing the structural properties of such equilibria, proving when they exist, and showing how they can be computed. Furthermore, we compare the sample complexity of incentive-aware collaboration with that of optimal collaboration when one ignores agents' incentives.