Look Within or Look Beyond? A Theoretical Comparison Between Parameter-Efficient and Full Fine-Tuning

Parameter-Efficient Fine-Tuning (PEFT) methods achieve performance comparable to Full Fine-Tuning (FFT) while requiring significantly fewer computing resources, making it the go-to choice for researchers. We find that although PEFT can achieve competitive results on some benchmarks, its performance falls short of FFT in complex tasks, such as reasoning and instruction-based fine-tuning. In this paper, we compare the characteristics of PEFT and FFT in terms of representational capacity and robustness based on optimization theory. We theoretically demonstrate that PEFT is a strict subset of FFT. By providing theoretical upper bounds for PEFT, we show that the limited parameter space constrains the model's representational ability, making it more susceptible to perturbations. Experiments on 15 datasets encompassing classification, generation, reasoning, instruction fine-tuning tasks and 11 adversarial test sets validate our theories. We hope that these results spark further research beyond the realms of well established PEFT. The source code is in the anonymous Github repository\footnote{https://github.com/misonsky/PEFTEval}.

Why Do More Experts Fail? A Theoretical Analysis of Model Merging

Model merging dramatically reduces storage and computational resources by combining multiple expert models into a single multi-task model. Although recent model merging methods have shown promising results, they struggle to maintain performance gains as the number of merged models increases. In this paper, we investigate the key obstacles that limit the scalability of model merging when integrating a large number of expert models. First, we prove that there is an upper bound on model merging. Further theoretical analysis reveals that the limited effective parameter space imposes a strict constraint on the number of models that can be successfully merged. Gaussian Width shows that the marginal benefit of merging additional models diminishes according to a strictly concave function. This implies that the effective parameter space becomes rapidly saturated as the number of merged models increases. Furthermore, using Approximate Kinematics Theory, we prove the existence of a unique optimal threshold beyond which adding more models does not yield significant performance improvements. At the same time, we introduce a straightforward Reparameterized Heavy-Tailed method (RHT) to extend the coverage of the merged model, thereby enhancing its performance. Empirical results on 12 benchmarks, including both knowledge-intensive and general-purpose tasks, validate our theoretical analysis. We believe that these results spark further research beyond the current scope of model merging. The source code is in the anonymous Github repository https://github.com/wzj1718/ModelMergingAnalysis.

Affective Computing in the Era of Large Language Models: A Survey from the NLP Perspective

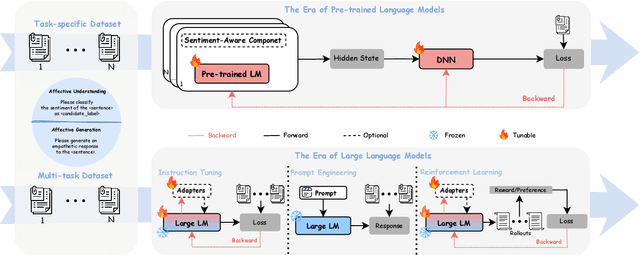
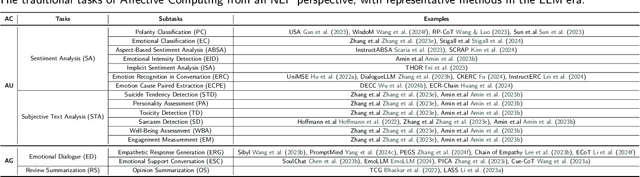
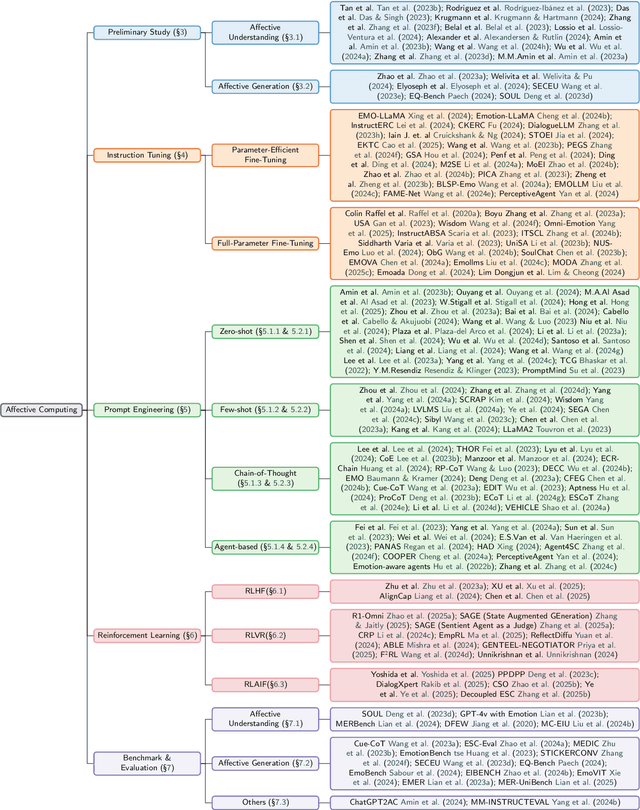
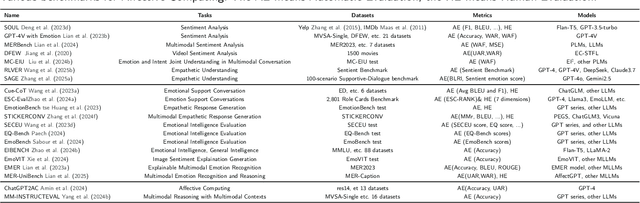
Affective Computing (AC), integrating computer science, psychology, and cognitive science knowledge, aims to enable machines to recognize, interpret, and simulate human emotions.To create more value, AC can be applied to diverse scenarios, including social media, finance, healthcare, education, etc. Affective Computing (AC) includes two mainstream tasks, i.e., Affective Understanding (AU) and Affective Generation (AG). Fine-tuning Pre-trained Language Models (PLMs) for AU tasks has succeeded considerably. However, these models lack generalization ability, requiring specialized models for specific tasks. Additionally, traditional PLMs face challenges in AG, particularly in generating diverse and emotionally rich responses. The emergence of Large Language Models (LLMs), such as the ChatGPT series and LLaMA models, brings new opportunities and challenges, catalyzing a paradigm shift in AC. LLMs possess capabilities of in-context learning, common sense reasoning, and advanced sequence generation, which present unprecedented opportunities for AU. To provide a comprehensive overview of AC in the LLMs era from an NLP perspective, we summarize the development of LLMs research in this field, aiming to offer new insights. Specifically, we first summarize the traditional tasks related to AC and introduce the preliminary study based on LLMs. Subsequently, we outline the relevant techniques of popular LLMs to improve AC tasks, including Instruction Tuning and Prompt Engineering. For Instruction Tuning, we discuss full parameter fine-tuning and parameter-efficient methods such as LoRA, P-Tuning, and Prompt Tuning. In Prompt Engineering, we examine Zero-shot, Few-shot, Chain of Thought (CoT), and Agent-based methods for AU and AG. To clearly understand the performance of LLMs on different Affective Computing tasks, we further summarize the existing benchmarks and evaluation methods.