Localized Diffusion Models for High Dimensional Distributions Generation

Diffusion models are the state-of-the-art tools for various generative tasks. However, estimating high-dimensional score functions makes them potentially suffer from the curse of dimensionality (CoD). This underscores the importance of better understanding and exploiting low-dimensional structure in the target distribution. In this work, we consider locality structure, which describes sparse dependencies between model components. Under locality structure, the score function is effectively low-dimensional, so that it can be estimated by a localized neural network with significantly reduced sample complexity. This motivates the localized diffusion model, where a localized score matching loss is used to train the score function within a localized hypothesis space. We prove that such localization enables diffusion models to circumvent CoD, at the price of additional localization error. Under realistic sample size scaling, we show both theoretically and numerically that a moderate localization radius can balance the statistical and localization error, leading to a better overall performance. The localized structure also facilitates parallel training of diffusion models, making it potentially more efficient for large-scale applications.

Resolving Memorization in Empirical Diffusion Model for Manifold Data in High-Dimensional Spaces

Diffusion models is a popular computational tool to generate new data samples. It utilizes a forward diffusion process that add noise to the data distribution and then use a reverse process to remove noises to produce samples from the data distribution. However, when the empirical data distribution consists of $n$ data point, using the empirical diffusion model will necessarily produce one of the existing data points. This is often referred to as the memorization effect, which is usually resolved by sophisticated machine learning procedures in the current literature. This work shows that the memorization problem can be resolved by a simple inertia update step at the end of the empirical diffusion model simulation. Our inertial diffusion model requires only the empirical diffusion model score function and it does not require any further training. We show that choosing the inertia diffusion model sample distribution is an $O\left(n^{-\frac{2}{d+4}}\right)$ Wasserstein-1 approximation of a data distribution lying on a $C^2$ manifold of dimension $d$. Since this estimate is significant smaller the Wasserstein1 distance between population and empirical distributions, it rigorously shows the inertial diffusion model produces new data samples. Remarkably, this upper bound is completely free of the ambient space dimension, since there is no training involved. Our analysis utilizes the fact that the inertial diffusion model samples are approximately distributed as the Gaussian kernel density estimator on the manifold. This reveals an interesting connection between diffusion model and manifold learning.

Demystifying the Token Dynamics of Deep Selective State Space Models

Selective state space models (SSM), such as Mamba, have gained prominence for their effectiveness in modeling sequential data. Despite their outstanding empirical performance, a comprehensive theoretical understanding of deep selective SSM remains elusive, hindering their further development and adoption for applications that need high fidelity. In this paper, we investigate the dynamical properties of tokens in a pre-trained Mamba model. In particular, we derive the dynamical system governing the continuous-time limit of the Mamba model and characterize the asymptotic behavior of its solutions. In the one-dimensional case, we prove that only one of the following two scenarios happens: either all tokens converge to zero, or all tokens diverge to infinity. We provide criteria based on model parameters to determine when each scenario occurs. For the convergent scenario, we empirically verify that this scenario negatively impacts the model's performance. For the divergent scenario, we prove that different tokens will diverge to infinity at different rates, thereby contributing unequally to the updates during model training. Based on these investigations, we propose two refinements for the model: excluding the convergent scenario and reordering tokens based on their importance scores, both aimed at improving practical performance. Our experimental results validate these refinements, offering insights into enhancing Mamba's effectiveness in real-world applications.

Stochastic Gradient Descent with Adaptive Data

Stochastic gradient descent (SGD) is a powerful optimization technique that is particularly useful in online learning scenarios. Its convergence analysis is relatively well understood under the assumption that the data samples are independent and identically distributed (iid). However, applying SGD to policy optimization problems in operations research involves a distinct challenge: the policy changes the environment and thereby affects the data used to update the policy. The adaptively generated data stream involves samples that are non-stationary, no longer independent from each other, and affected by previous decisions. The influence of previous decisions on the data generated introduces bias in the gradient estimate, which presents a potential source of instability for online learning not present in the iid case. In this paper, we introduce simple criteria for the adaptively generated data stream to guarantee the convergence of SGD. We show that the convergence speed of SGD with adaptive data is largely similar to the classical iid setting, as long as the mixing time of the policy-induced dynamics is factored in. Our Lyapunov-function analysis allows one to translate existing stability analysis of stochastic systems studied in operations research into convergence rates for SGD, and we demonstrate this for queueing and inventory management problems. We also showcase how our result can be applied to study the sample complexity of an actor-critic policy gradient algorithm.

Wasserstein gradient flow for optimal probability measure decomposition

We examine the infinite-dimensional optimization problem of finding a decomposition of a probability measure into K probability sub-measures to minimize specific loss functions inspired by applications in clustering and user grouping. We analytically explore the structures of the support of optimal sub-measures and introduce algorithms based on Wasserstein gradient flow, demonstrating their convergence. Numerical results illustrate the implementability of our algorithms and provide further insights.

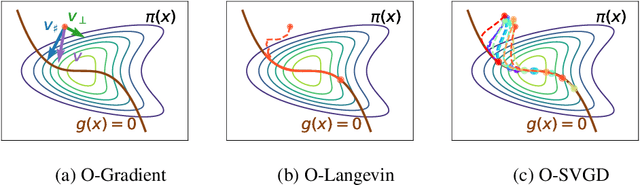
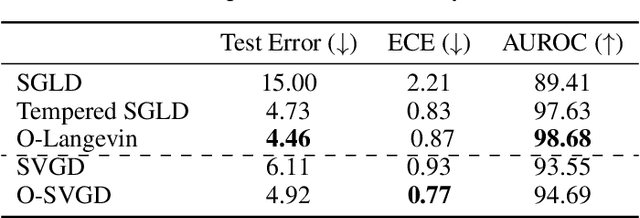
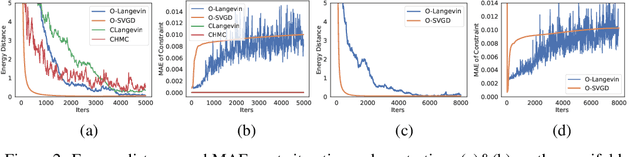
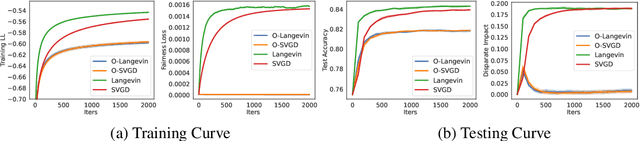
Sampling in Constrained Domains with Orthogonal-Space Variational Gradient Descent

Sampling methods, as important inference and learning techniques, are typically designed for unconstrained domains. However, constraints are ubiquitous in machine learning problems, such as those on safety, fairness, robustness, and many other properties that must be satisfied to apply sampling results in real-life applications. Enforcing these constraints often leads to implicitly-defined manifolds, making efficient sampling with constraints very challenging. In this paper, we propose a new variational framework with a designed orthogonal-space gradient flow (O-Gradient) for sampling on a manifold $\mathcal{G}_0$ defined by general equality constraints. O-Gradient decomposes the gradient into two parts: one decreases the distance to $\mathcal{G}_0$ and the other decreases the KL divergence in the orthogonal space. While most existing manifold sampling methods require initialization on $\mathcal{G}_0$, O-Gradient does not require such prior knowledge. We prove that O-Gradient converges to the target constrained distribution with rate $\widetilde{O}(1/\text{the number of iterations})$ under mild conditions. Our proof relies on a new Stein characterization of conditional measure which could be of independent interest. We implement O-Gradient through both Langevin dynamics and Stein variational gradient descent and demonstrate its effectiveness in various experiments, including Bayesian deep neural networks.

Can We Do Better Than Random Start? The Power of Data Outsourcing

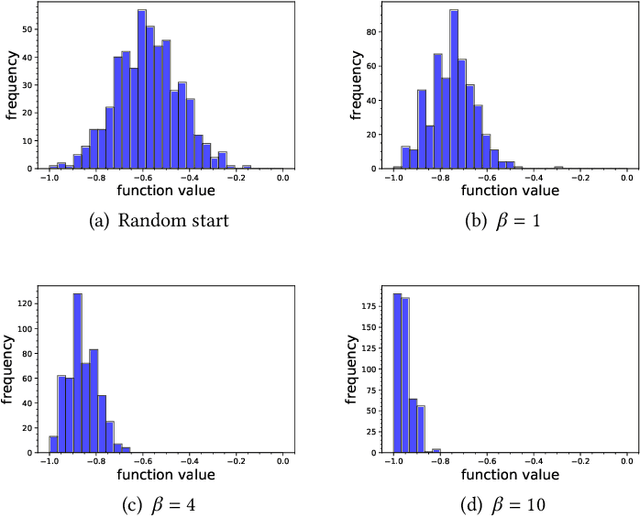
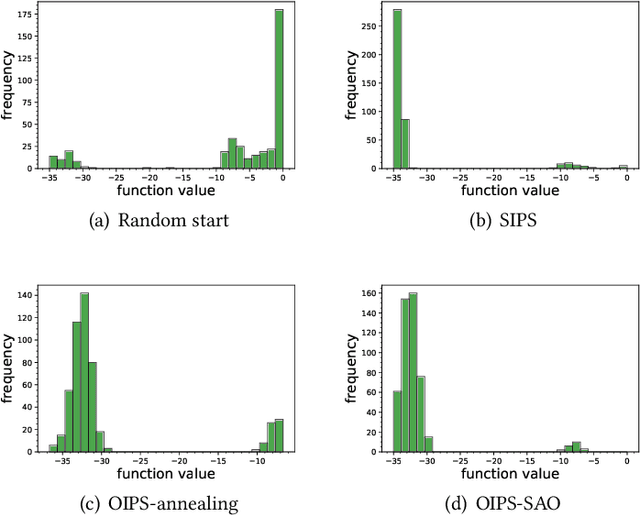
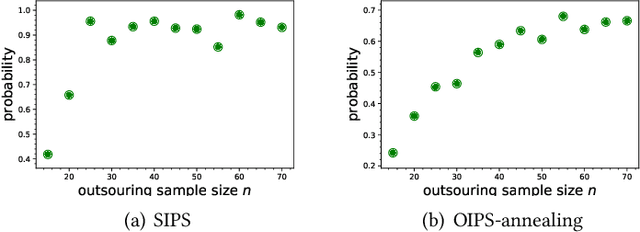
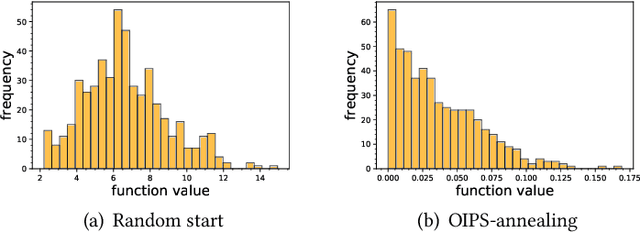
Many organizations have access to abundant data but lack the computational power to process the data. While they can outsource the computational task to other facilities, there are various constraints on the amount of data that can be shared. It is natural to ask what can data outsourcing accomplish under such constraints. We address this question from a machine learning perspective. When training a model with optimization algorithms, the quality of the results often relies heavily on the points where the algorithms are initialized. Random start is one of the most popular methods to tackle this issue, but it can be computationally expensive and not feasible for organizations lacking computing resources. Based on three different scenarios, we propose simulation-based algorithms that can utilize a small amount of outsourced data to find good initial points accordingly. Under suitable regularity conditions, we provide theoretical guarantees showing the algorithms can find good initial points with high probability. We also conduct numerical experiments to demonstrate that our algorithms perform significantly better than the random start approach.

Stochastic Gradient Descent with Dependent Data for Offline Reinforcement Learning

In reinforcement learning (RL), offline learning decoupled learning from data collection and is useful in dealing with exploration-exploitation tradeoff and enables data reuse in many applications. In this work, we study two offline learning tasks: policy evaluation and policy learning. For policy evaluation, we formulate it as a stochastic optimization problem and show that it can be solved using approximate stochastic gradient descent (aSGD) with time-dependent data. We show aSGD achieves $\tilde O(1/t)$ convergence when the loss function is strongly convex and the rate is independent of the discount factor $\gamma$. This result can be extended to include algorithms making approximately contractive iterations such as TD(0). The policy evaluation algorithm is then combined with the policy iteration algorithm to learn the optimal policy. To achieve an $\epsilon$ accuracy, the complexity of the algorithm is $\tilde O(\epsilon^{-2}(1-\gamma)^{-5})$, which matches the complexity bound for classic online RL algorithms such as Q-learning.

Consistency analysis of bilevel data-driven learning in inverse problems

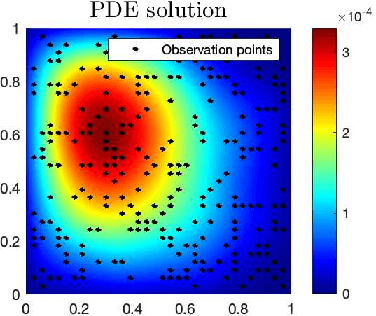
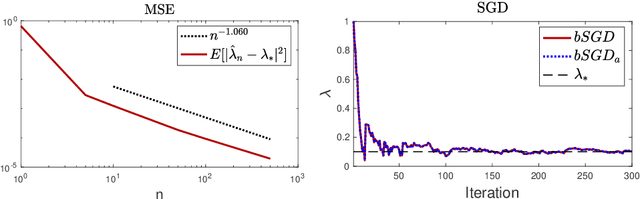
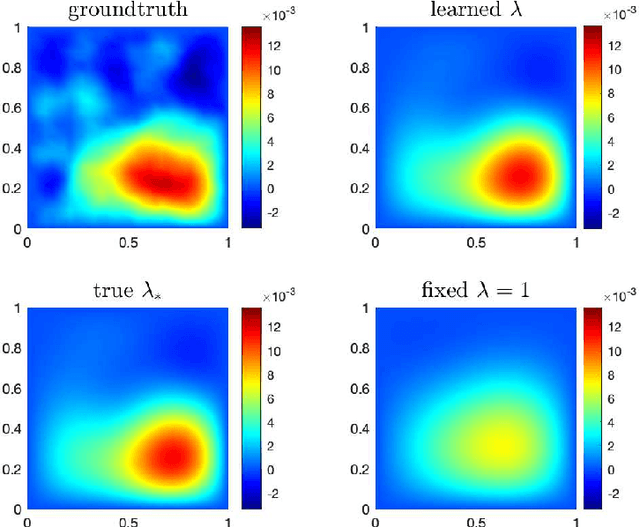
One fundamental problem when solving inverse problems is how to find regularization parameters. This article considers solving this problem using data-driven bilevel optimization, i.e. we consider the adaptive learning of the regularization parameter from data by means of optimization. This approach can be interpreted as solving an empirical risk minimization problem, and we analyze its performance in the large data sample size limit for general nonlinear problems. To reduce the associated computational cost, online numerical schemes are derived using the stochastic gradient method. We prove convergence of these numerical schemes under suitable assumptions on the forward problem. Numerical experiments are presented illustrating the theoretical results and demonstrating the applicability and efficiency of the proposed approaches for various linear and nonlinear inverse problems, including Darcy flow, the eikonal equation, and an image denoising example.

Dimension Independent Generalization Error with Regularized Online Optimization

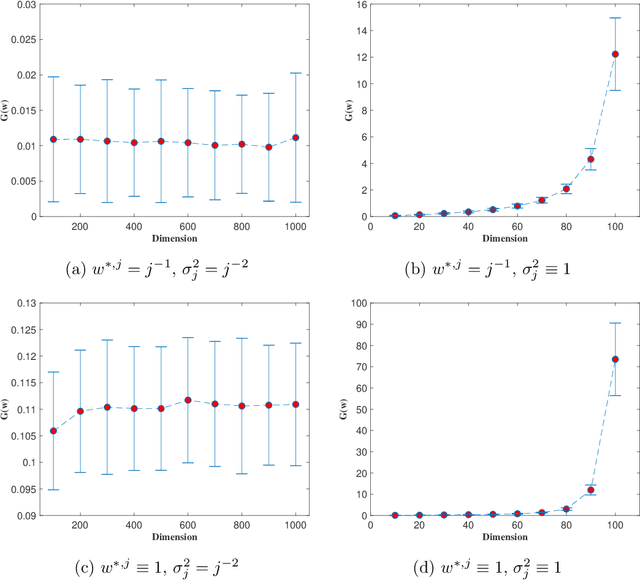
One classical canon of statistics is that large models are prone to overfitting and model selection procedures are necessary for high-dimensional data. However, many overparameterized models such as neural networks, which are often trained with simple online methods and regularization, perform very well in practice. The empirical success of overparameterized models, which is often known as benign overfitting, motivates us to have a new look at the statistical generalization theory for online optimization. In particular, we present a general theory on the generalization error of stochastic gradient descent (SGD) for both convex and non-convex loss functions. We further provide the definition of "low effective dimension" so that the generalization error either does not depend on the ambient dimension $p$ or depends on $p$ via a poly-logarithmic factor. We also demonstrate on several widely used statistical models that the "low effect dimension" arises naturally in overparameterized settings. The studied statistical applications include both convex models such as linear regression and logistic regression, and non-convex models such as $M$-estimator and two-layer neural networks.