Learning dynamical systems from data: Gradient-based dictionary optimization

The Koopman operator plays a crucial role in analyzing the global behavior of dynamical systems. Existing data-driven methods for approximating the Koopman operator or discovering the governing equations of the underlying system typically require a fixed set of basis functions, also called dictionary. The optimal choice of basis functions is highly problem-dependent and often requires domain knowledge. We present a novel gradient descent-based optimization framework for learning suitable and interpretable basis functions from data and show how it can be used in combination with EDMD, SINDy, and PDE-FIND. We illustrate the efficacy of the proposed approach with the aid of various benchmark problems such as the Ornstein-Uhlenbeck process, Chua's circuit, a nonlinear heat equation, as well as protein-folding data.

Unbiased Kinetic Langevin Monte Carlo with Inexact Gradients

We present an unbiased method for Bayesian posterior means based on kinetic Langevin dynamics that combines advanced splitting methods with enhanced gradient approximations. Our approach avoids Metropolis correction by coupling Markov chains at different discretization levels in a multilevel Monte Carlo approach. Theoretical analysis demonstrates that our proposed estimator is unbiased, attains finite variance, and satisfies a central limit theorem. It can achieve accuracy $\epsilon>0$ for estimating expectations of Lipschitz functions in $d$ dimensions with $\mathcal{O}(d^{1/4}\epsilon^{-2})$ expected gradient evaluations, without assuming warm start. We exhibit similar bounds using both approximate and stochastic gradients, and our method's computational cost is shown to scale logarithmically with the size of the dataset. The proposed method is tested using a multinomial regression problem on the MNIST dataset and a Poisson regression model for soccer scores. Experiments indicate that the number of gradient evaluations per effective sample is independent of dimension, even when using inexact gradients. For product distributions, we give dimension-independent variance bounds. Our results demonstrate that the unbiased algorithm we present can be much more efficient than the ``gold-standard" randomized Hamiltonian Monte Carlo.

A Data-Adaptive Prior for Bayesian Learning of Kernels in Operators

Kernels are efficient in representing nonlocal dependence and they are widely used to design operators between function spaces. Thus, learning kernels in operators from data is an inverse problem of general interest. Due to the nonlocal dependence, the inverse problem can be severely ill-posed with a data-dependent singular inversion operator. The Bayesian approach overcomes the ill-posedness through a non-degenerate prior. However, a fixed non-degenerate prior leads to a divergent posterior mean when the observation noise becomes small, if the data induces a perturbation in the eigenspace of zero eigenvalues of the inversion operator. We introduce a data-adaptive prior to achieve a stable posterior whose mean always has a small noise limit. The data-adaptive prior's covariance is the inversion operator with a hyper-parameter selected adaptive to data by the L-curve method. Furthermore, we provide a detailed analysis on the computational practice of the data-adaptive prior, and demonstrate it on Toeplitz matrices and integral operators. Numerical tests show that a fixed prior can lead to a divergent posterior mean in the presence of any of the four types of errors: discretization error, model error, partial observation and wrong noise assumption. In contrast, the data-adaptive prior always attains posterior means with small noise limits.

Unbiased Estimation using the Underdamped Langevin Dynamics

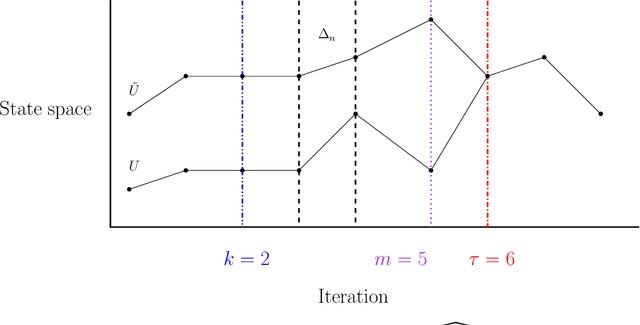
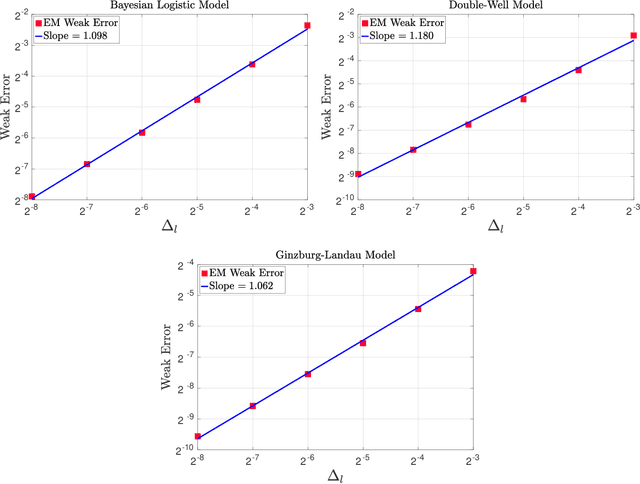
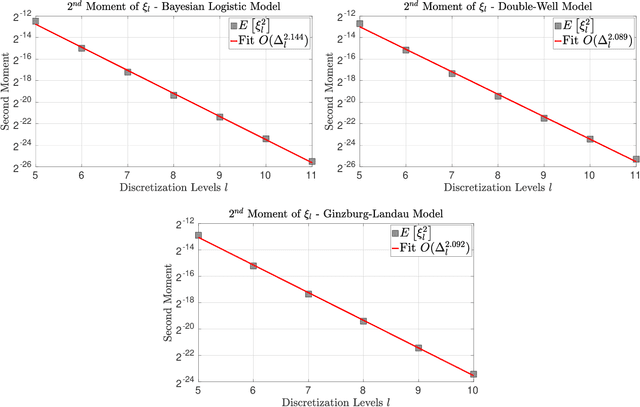
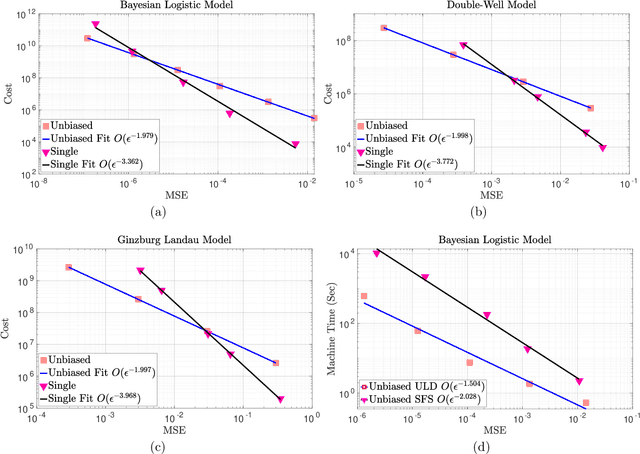
In this work we consider the unbiased estimation of expectations w.r.t.~probability measures that have non-negative Lebesgue density, and which are known point-wise up-to a normalizing constant. We focus upon developing an unbiased method via the underdamped Langevin dynamics, which has proven to be popular of late due to applications in statistics and machine learning. Specifically in continuous-time, the dynamics can be constructed to admit the probability of interest as a stationary measure. We develop a novel scheme based upon doubly randomized estimation, which requires access only to time-discretized versions of the dynamics and are the ones that are used in practical algorithms. We prove, under standard assumptions, that our estimator is of finite variance and either has finite expected cost, or has finite cost with a high probability. To illustrate our theoretical findings we provide numerical experiments that verify our theory, which include challenging examples from Bayesian statistics and statistical physics.

Multilevel Bayesian Deep Neural Networks

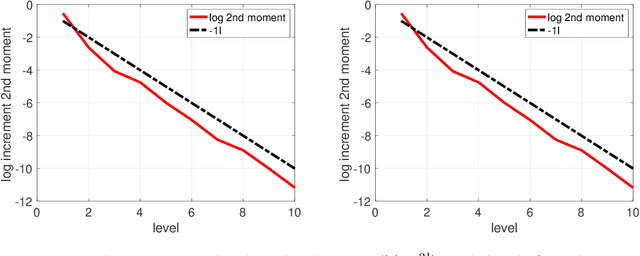
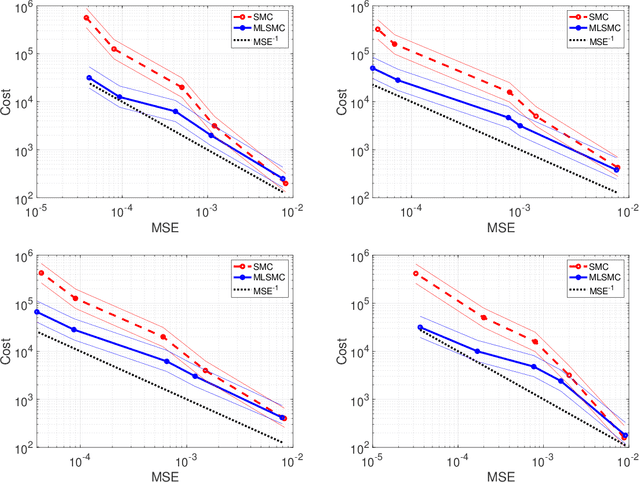
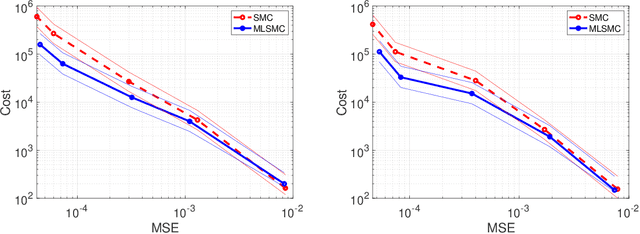
In this article we consider Bayesian inference associated to deep neural networks (DNNs) and in particular, trace-class neural network (TNN) priors which were proposed by Sell et al. [39]. Such priors were developed as more robust alternatives to classical architectures in the context of inference problems. For this work we develop multilevel Monte Carlo (MLMC) methods for such models. MLMC is a popular variance reduction technique, with particular applications in Bayesian statistics and uncertainty quantification. We show how a particular advanced MLMC method that was introduced in [4] can be applied to Bayesian inference from DNNs and establish mathematically, that the computational cost to achieve a particular mean square error, associated to posterior expectation computation, can be reduced by several orders, versus more conventional techniques. To verify such results we provide numerous numerical experiments on model problems arising in machine learning. These include Bayesian regression, as well as Bayesian classification and reinforcement learning.

Consistency analysis of bilevel data-driven learning in inverse problems

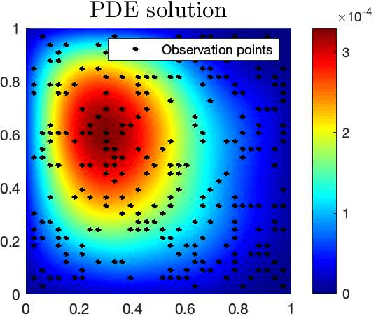
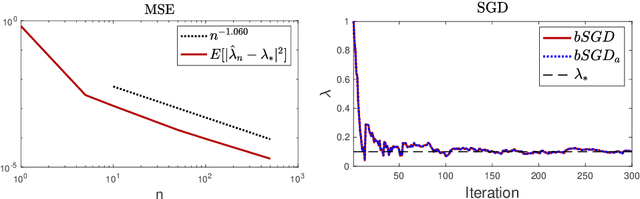
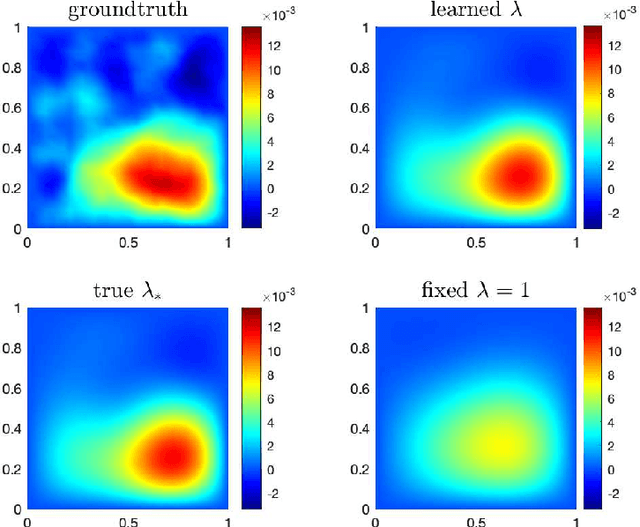
One fundamental problem when solving inverse problems is how to find regularization parameters. This article considers solving this problem using data-driven bilevel optimization, i.e. we consider the adaptive learning of the regularization parameter from data by means of optimization. This approach can be interpreted as solving an empirical risk minimization problem, and we analyze its performance in the large data sample size limit for general nonlinear problems. To reduce the associated computational cost, online numerical schemes are derived using the stochastic gradient method. We prove convergence of these numerical schemes under suitable assumptions on the forward problem. Numerical experiments are presented illustrating the theoretical results and demonstrating the applicability and efficiency of the proposed approaches for various linear and nonlinear inverse problems, including Darcy flow, the eikonal equation, and an image denoising example.