Learning Chaotic Dynamics with Neuromorphic Network Dynamics

This study investigates how dynamical systems may be learned and modelled with a neuromorphic network which is itself a dynamical system. The neuromorphic network used in this study is based on a complex electrical circuit comprised of memristive elements that produce neuro-synaptic nonlinear responses to input electrical signals. To determine how computation may be performed using the physics of the underlying system, the neuromorphic network was simulated and evaluated on autonomous prediction of a multivariate chaotic time series, implemented with a reservoir computing framework. Through manipulating only input electrodes and voltages, optimal nonlinear dynamical responses were found when input voltages maximise the number of memristive components whose internal dynamics explore the entire dynamical range of the memristor model. Increasing the network coverage with the input electrodes was found to suppress other nonlinear responses that are less conducive to learning. These results provide valuable insights into how a practical neuromorphic network device can be optimised for learning complex dynamical systems using only external control parameters.

UNO: Unlearning via Orthogonalization in Generative models

As generative models become increasingly powerful and pervasive, the ability to unlearn specific data, whether due to privacy concerns, legal requirements, or the correction of harmful content, has become increasingly important. Unlike in conventional training, where data are accumulated and knowledge is reinforced, unlearning aims to selectively remove the influence of particular data points without costly retraining from scratch. To be effective and reliable, such algorithms need to achieve (i) forgetting of the undesired data, (ii) preservation of the quality of the generation, (iii) preservation of the influence of the desired training data on the model parameters, and (iv) small number of training steps. We propose fast unlearning algorithms based on loss gradient orthogonalization. We show that our algorithms are able to forget data while maintaining the fidelity of the original model. Using MNIST and CelebA data, we demonstrate that our algorithms achieve orders of magnitude faster unlearning times than their predecessors, such as gradient surgery.

Dynamic Reservoir Computing with Physical Neuromorphic Networks

Reservoir Computing (RC) with physical systems requires an understanding of the underlying structure and internal dynamics of the specific physical reservoir. In this study, physical nano-electronic networks with neuromorphic dynamics are investigated for their use as physical reservoirs in an RC framework. These neuromorphic networks operate as dynamic reservoirs, with node activities in general coupled to the edge dynamics through nonlinear nano-electronic circuit elements, and the reservoir outputs influenced by the underlying network connectivity structure. This study finds that networks with varying degrees of sparsity generate more useful nonlinear temporal outputs for dynamic RC compared to dense networks. Dynamic RC is also tested on an autonomous multivariate chaotic time series prediction task with networks of varying densities, which revealed the importance of network sparsity in maintaining network activity and overall dynamics, that in turn enabled the learning of the chaotic Lorenz63 system's attractor behavior.

Localized Diffusion Models for High Dimensional Distributions Generation

Diffusion models are the state-of-the-art tools for various generative tasks. However, estimating high-dimensional score functions makes them potentially suffer from the curse of dimensionality (CoD). This underscores the importance of better understanding and exploiting low-dimensional structure in the target distribution. In this work, we consider locality structure, which describes sparse dependencies between model components. Under locality structure, the score function is effectively low-dimensional, so that it can be estimated by a localized neural network with significantly reduced sample complexity. This motivates the localized diffusion model, where a localized score matching loss is used to train the score function within a localized hypothesis space. We prove that such localization enables diffusion models to circumvent CoD, at the price of additional localization error. Under realistic sample size scaling, we show both theoretically and numerically that a moderate localization radius can balance the statistical and localization error, leading to a better overall performance. The localized structure also facilitates parallel training of diffusion models, making it potentially more efficient for large-scale applications.

Learning dynamical systems with hit-and-run random feature maps

We show how random feature maps can be used to forecast dynamical systems with excellent forecasting skill. We consider the tanh activation function and judiciously choose the internal weights in a data-driven manner such that the resulting features explore the nonlinear, non-saturated regions of the activation function. We introduce skip connections and construct a deep variant of random feature maps by combining several units. To mitigate the curse of dimensionality, we introduce localization where we learn local maps, employing conditional independence. Our modified random feature maps provide excellent forecasting skill for both single trajectory forecasts as well as long-time estimates of statistical properties, for a range of chaotic dynamical systems with dimensions up to 512. In contrast to other methods such as reservoir computers which require extensive hyperparameter tuning, we effectively need to tune only a single hyperparameter, and are able to achieve state-of-the-art forecast skill with much smaller networks.

Localized Schrödinger Bridge Sampler

We consider the generative problem of sampling from an unknown distribution for which only a sufficiently large number of training samples are available. In this paper, we build on previous work combining Schr\"odinger bridges and Langevin dynamics. A key bottleneck of this approach is the exponential dependence of the required training samples on the dimension, $d$, of the ambient state space. We propose a localization strategy which exploits conditional independence of conditional expectation values. Localization thus replaces a single high-dimensional Schr\"odinger bridge problem by $d$ low-dimensional Schr\"odinger bridge problems over the available training samples. As for the original approach, the localized sampler is stable and geometric ergodic. The sampler also naturally extends to conditional sampling and to Bayesian inference. We demonstrate the performance of our proposed scheme through experiments on a Gaussian problem with increasing dimensions and on a stochastic subgrid-scale parametrization conditional sampling problem.

On the choice of the non-trainable internal weights in random feature maps

The computationally cheap machine learning architecture of random feature maps can be viewed as a single-layer feedforward network in which the weights of the hidden layer are random but fixed and only the outer weights are learned via linear regression. The internal weights are typically chosen from a prescribed distribution. The choice of the internal weights significantly impacts the accuracy of random feature maps. We address here the task of how to best select the internal weights. In particular, we consider the forecasting problem whereby random feature maps are used to learn a one-step propagator map for a dynamical system. We provide a computationally cheap hit-and-run algorithm to select good internal weights which lead to good forecasting skill. We show that the number of good features is the main factor controlling the forecasting skill of random feature maps and acts as an effective feature dimension. Lastly, we compare random feature maps with single-layer feedforward neural networks in which the internal weights are now learned using gradient descent. We find that random feature maps have superior forecasting capabilities whilst having several orders of magnitude lower computational cost.

Combining machine learning and data assimilation to forecast dynamical systems from noisy partial observations

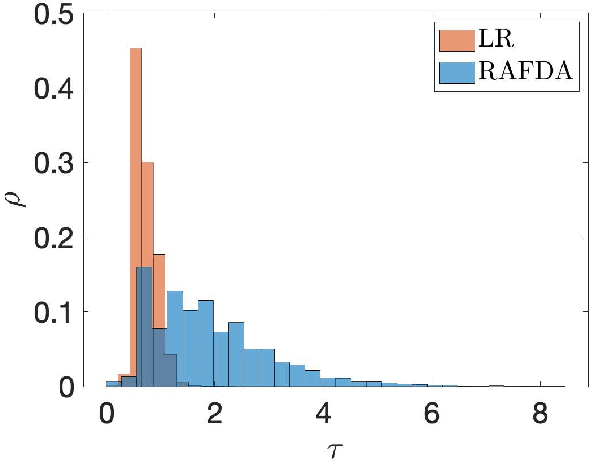
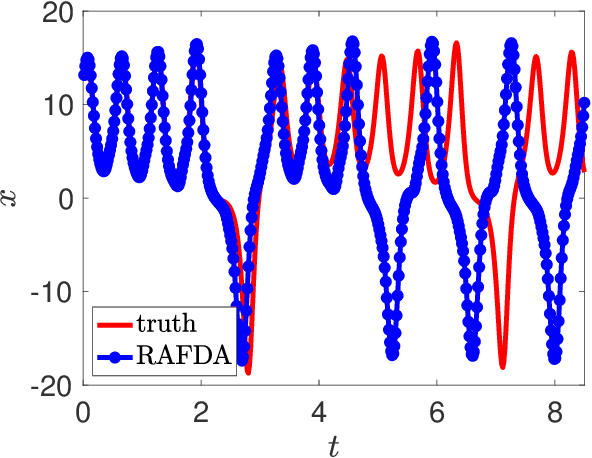
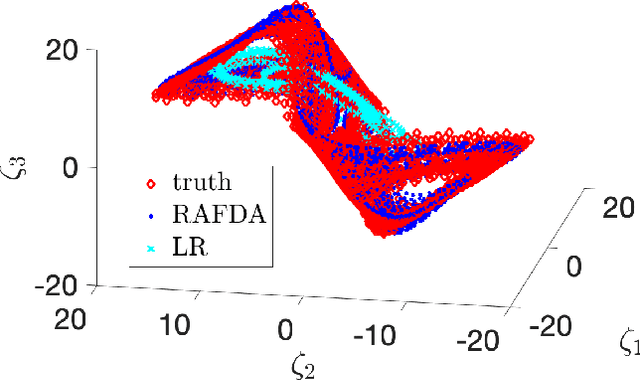
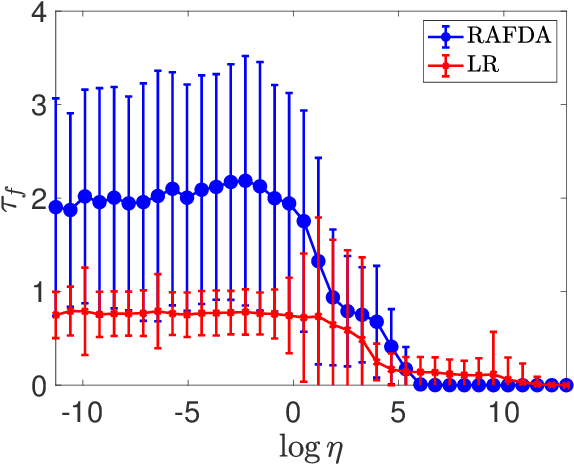
We present a supervised learning method to learn the propagator map of a dynamical system from partial and noisy observations. In our computationally cheap and easy-to-implement framework a neural network consisting of random feature maps is trained sequentially by incoming observations within a data assimilation procedure. By employing Takens' embedding theorem, the network is trained on delay coordinates. We show that the combination of random feature maps and data assimilation, called RAFDA, outperforms standard random feature maps for which the dynamics is learned using batch data.

Supervised learning from noisy observations: Combining machine-learning techniques with data assimilation

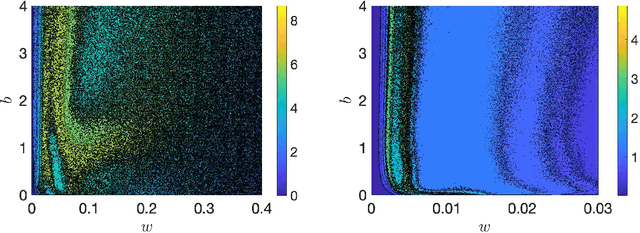
Data-driven prediction and physics-agnostic machine-learning methods have attracted increased interest in recent years achieving forecast horizons going well beyond those to be expected for chaotic dynamical systems. In a separate strand of research data-assimilation has been successfully used to optimally combine forecast models and their inherent uncertainty with incoming noisy observations. The key idea in our work here is to achieve increased forecast capabilities by judiciously combining machine-learning algorithms and data assimilation. We combine the physics-agnostic data-driven approach of random feature maps as a forecast model within an ensemble Kalman filter data assimilation procedure. The machine-learning model is learned sequentially by incorporating incoming noisy observations. We show that the obtained forecast model has remarkably good forecast skill while being computationally cheap once trained. Going beyond the task of forecasting, we show that our method can be used to generate reliable ensembles for probabilistic forecasting as well as to learn effective model closure in multi-scale systems.