Xiaoou Tang
Recover Canonical-View Faces in the Wild with Deep Neural Networks
Apr 16, 2014
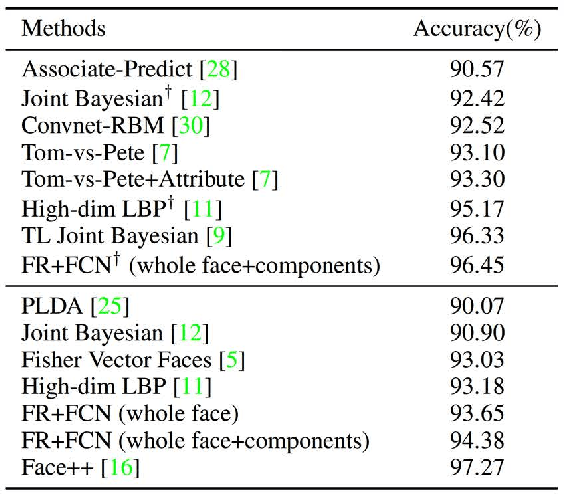

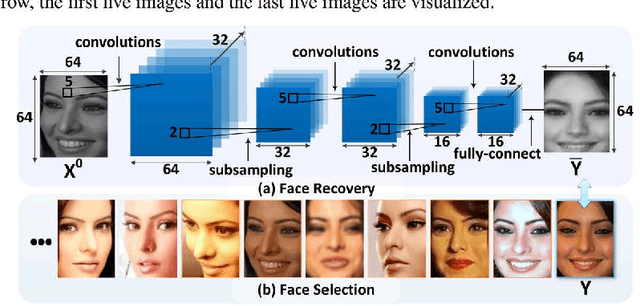
Abstract:Face images in the wild undergo large intra-personal variations, such as poses, illuminations, occlusions, and low resolutions, which cause great challenges to face-related applications. This paper addresses this challenge by proposing a new deep learning framework that can recover the canonical view of face images. It dramatically reduces the intra-person variances, while maintaining the inter-person discriminativeness. Unlike the existing face reconstruction methods that were either evaluated in controlled 2D environment or employed 3D information, our approach directly learns the transformation from the face images with a complex set of variations to their canonical views. At the training stage, to avoid the costly process of labeling canonical-view images from the training set by hand, we have devised a new measurement to automatically select or synthesize a canonical-view image for each identity. As an application, this face recovery approach is used for face verification. Facial features are learned from the recovered canonical-view face images by using a facial component-based convolutional neural network. Our approach achieves the state-of-the-art performance on the LFW dataset.
Graph Degree Linkage: Agglomerative Clustering on a Directed Graph
Aug 25, 2012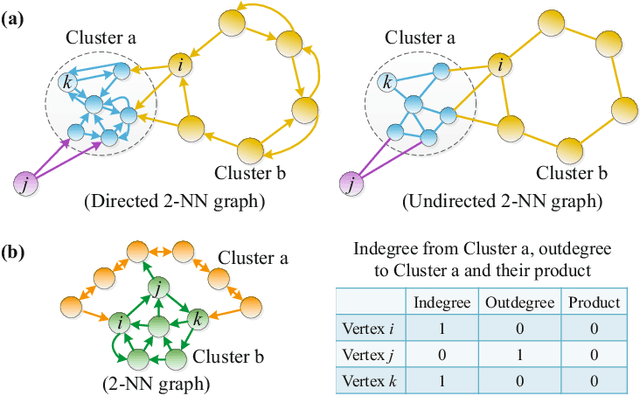
Abstract:This paper proposes a simple but effective graph-based agglomerative algorithm, for clustering high-dimensional data. We explore the different roles of two fundamental concepts in graph theory, indegree and outdegree, in the context of clustering. The average indegree reflects the density near a sample, and the average outdegree characterizes the local geometry around a sample. Based on such insights, we define the affinity measure of clusters via the product of average indegree and average outdegree. The product-based affinity makes our algorithm robust to noise. The algorithm has three main advantages: good performance, easy implementation, and high computational efficiency. We test the algorithm on two fundamental computer vision problems: image clustering and object matching. Extensive experiments demonstrate that it outperforms the state-of-the-arts in both applications.
Clustering with Transitive Distance and K-Means Duality
Nov 22, 2007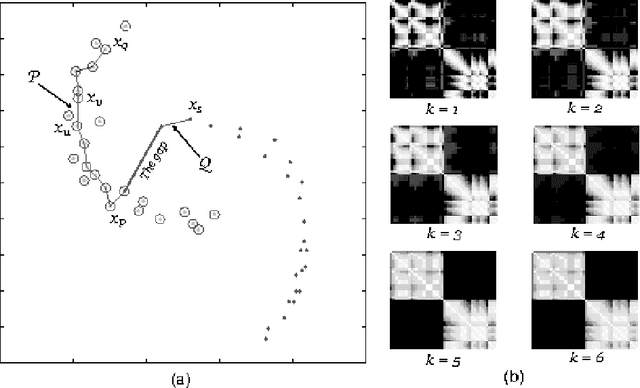

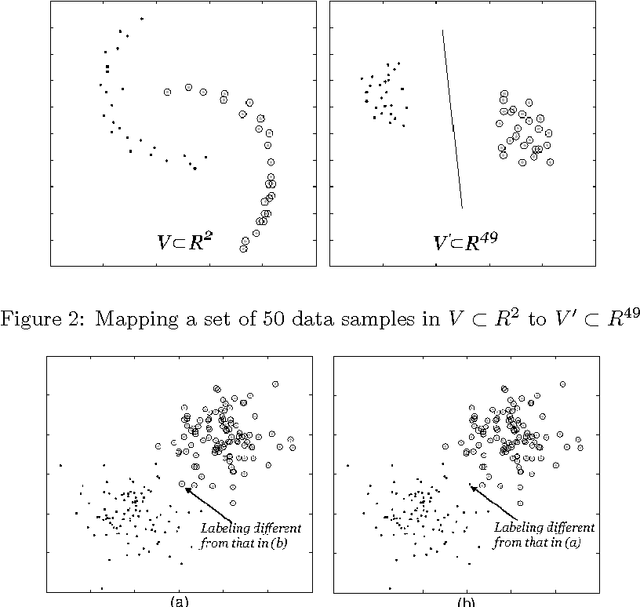
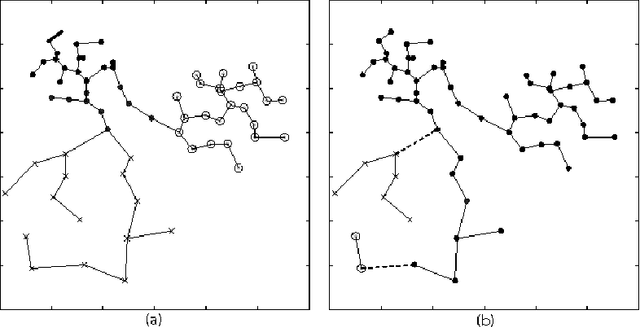
Abstract:Recent spectral clustering methods are a propular and powerful technique for data clustering. These methods need to solve the eigenproblem whose computational complexity is $O(n^3)$, where $n$ is the number of data samples. In this paper, a non-eigenproblem based clustering method is proposed to deal with the clustering problem. Its performance is comparable to the spectral clustering algorithms but it is more efficient with computational complexity $O(n^2)$. We show that with a transitive distance and an observed property, called K-means duality, our algorithm can be used to handle data sets with complex cluster shapes, multi-scale clusters, and noise. Moreover, no parameters except the number of clusters need to be set in our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge