Finite-Time Frequentist Regret Bounds of Multi-Agent Thompson Sampling on Sparse Hypergraphs

We study the multi-agent multi-armed bandit (MAMAB) problem, where $m$ agents are factored into $\rho$ overlapping groups. Each group represents a hyperedge, forming a hypergraph over the agents. At each round of interaction, the learner pulls a joint arm (composed of individual arms for each agent) and receives a reward according to the hypergraph structure. Specifically, we assume there is a local reward for each hyperedge, and the reward of the joint arm is the sum of these local rewards. Previous work introduced the multi-agent Thompson sampling (MATS) algorithm \citep{verstraeten2020multiagent} and derived a Bayesian regret bound. However, it remains an open problem how to derive a frequentist regret bound for Thompson sampling in this multi-agent setting. To address these issues, we propose an efficient variant of MATS, the $\epsilon$-exploring Multi-Agent Thompson Sampling ($\epsilon$-MATS) algorithm, which performs MATS exploration with probability $\epsilon$ while adopts a greedy policy otherwise. We prove that $\epsilon$-MATS achieves a worst-case frequentist regret bound that is sublinear in both the time horizon and the local arm size. We also derive a lower bound for this setting, which implies our frequentist regret upper bound is optimal up to constant and logarithm terms, when the hypergraph is sufficiently sparse. Thorough experiments on standard MAMAB problems demonstrate the superior performance and the improved computational efficiency of $\epsilon$-MATS compared with existing algorithms in the same setting.

Optimal Cooperative Multiplayer Learning Bandits with Noisy Rewards and No Communication

We consider a cooperative multiplayer bandit learning problem where the players are only allowed to agree on a strategy beforehand, but cannot communicate during the learning process. In this problem, each player simultaneously selects an action. Based on the actions selected by all players, the team of players receives a reward. The actions of all the players are commonly observed. However, each player receives a noisy version of the reward which cannot be shared with other players. Since players receive potentially different rewards, there is an asymmetry in the information used to select their actions. In this paper, we provide an algorithm based on upper and lower confidence bounds that the players can use to select their optimal actions despite the asymmetry in the reward information. We show that this algorithm can achieve logarithmic $O(\frac{\log T}{\Delta_{\bm{a}}})$ (gap-dependent) regret as well as $O(\sqrt{T\log T})$ (gap-independent) regret. This is asymptotically optimal in $T$. We also show that it performs empirically better than the current state of the art algorithm for this environment.

No-Regret Online Reinforcement Learning with Adversarial Losses and Transitions

Existing online learning algorithms for adversarial Markov Decision Processes achieve ${O}(\sqrt{T})$ regret after $T$ rounds of interactions even if the loss functions are chosen arbitrarily by an adversary, with the caveat that the transition function has to be fixed. This is because it has been shown that adversarial transition functions make no-regret learning impossible. Despite such impossibility results, in this work, we develop algorithms that can handle both adversarial losses and adversarial transitions, with regret increasing smoothly in the degree of maliciousness of the adversary. More concretely, we first propose an algorithm that enjoys $\widetilde{{O}}(\sqrt{T} + C^{\textsf{P}})$ regret where $C^{\textsf{P}}$ measures how adversarial the transition functions are and can be at most ${O}(T)$. While this algorithm itself requires knowledge of $C^{\textsf{P}}$, we further develop a black-box reduction approach that removes this requirement. Moreover, we also show that further refinements of the algorithm not only maintains the same regret bound, but also simultaneously adapts to easier environments (where losses are generated in a certain stochastically constrained manner as in Jin et al. [2021]) and achieves $\widetilde{{O}}(U + \sqrt{UC^{\textsf{L}}} + C^{\textsf{P}})$ regret, where $U$ is some standard gap-dependent coefficient and $C^{\textsf{L}}$ is the amount of corruption on losses.

Approximation Capabilities of Neural Networks using Morphological Perceptrons and Generalizations

Standard artificial neural networks (ANNs) use sum-product or multiply-accumulate node operations with a memoryless nonlinear activation. These neural networks are known to have universal function approximation capabilities. Previously proposed morphological perceptrons use max-sum, in place of sum-product, node processing and have promising properties for circuit implementations. In this paper we show that these max-sum ANNs do not have universal approximation capabilities. Furthermore, we consider proposed signed-max-sum and max-star-sum generalizations of morphological ANNs and show that these variants also do not have universal approximation capabilities. We contrast these variations to log-number system (LNS) implementations which also avoid multiplications, but do exhibit universal approximation capabilities.

Online Learning for Cooperative Multi-Player Multi-Armed Bandits

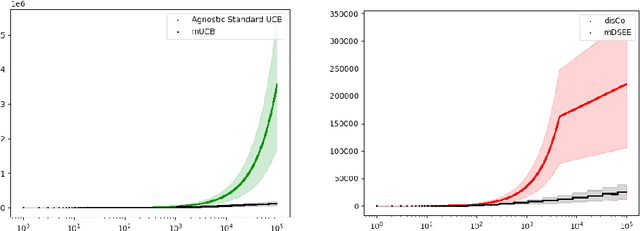
We introduce a framework for decentralized online learning for multi-armed bandits (MAB) with multiple cooperative players. The reward obtained by the players in each round depends on the actions taken by all the players. It's a team setting, and the objective is common. Information asymmetry is what makes the problem interesting and challenging. We consider three types of information asymmetry: action information asymmetry when the actions of the players can't be observed but the rewards received are common; reward information asymmetry when the actions of the other players are observable but rewards received are IID from the same distribution; and when we have both action and reward information asymmetry. For the first setting, we propose a UCB-inspired algorithm that achieves $O(\log T)$ regret whether the rewards are IID or Markovian. For the second section, we offer an environment such that the algorithm given for the first setting gives linear regret. For the third setting, we show that a variation of the `explore then commit' algorithm achieves almost log regret.

Toward Automatic Threat Recognition for Airport X-ray Baggage Screening with Deep Convolutional Object Detection

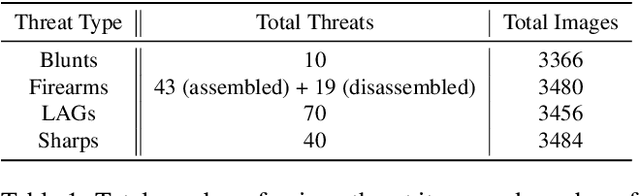
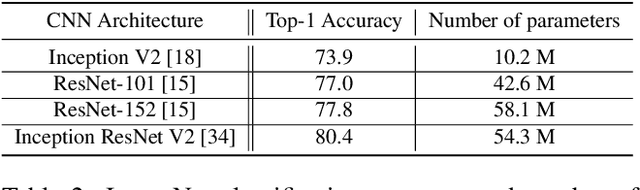
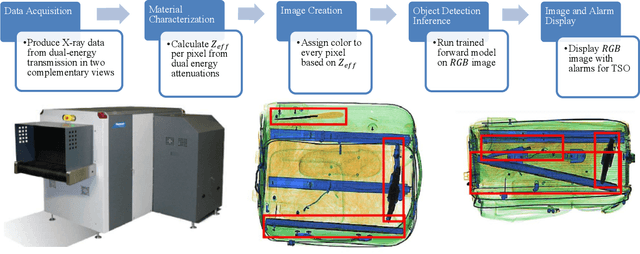
For the safety of the traveling public, the Transportation Security Administration (TSA) operates security checkpoints at airports in the United States, seeking to keep dangerous items off airplanes. At these checkpoints, the TSA employs a fleet of X-ray scanners, such as the Rapiscan 620DV, so Transportation Security Officers (TSOs) can inspect the contents of carry-on possessions. However, identifying and locating all potential threats can be a challenging task. As a result, the TSA has taken a recent interest in deep learning-based automated detection algorithms that can assist TSOs. In a collaboration funded by the TSA, we collected a sizable new dataset of X-ray scans with a diverse set of threats in a wide array of contexts, trained several deep convolutional object detection models, and integrated such models into the Rapiscan 620DV, resulting in functional prototypes capable of operating in real time. We show performance of our models on held-out evaluation sets, analyze several design parameters, and demonstrate the potential of such systems for automated detection of threats that can be found in airports.