No-Regret Online Reinforcement Learning with Adversarial Losses and Transitions

Existing online learning algorithms for adversarial Markov Decision Processes achieve ${O}(\sqrt{T})$ regret after $T$ rounds of interactions even if the loss functions are chosen arbitrarily by an adversary, with the caveat that the transition function has to be fixed. This is because it has been shown that adversarial transition functions make no-regret learning impossible. Despite such impossibility results, in this work, we develop algorithms that can handle both adversarial losses and adversarial transitions, with regret increasing smoothly in the degree of maliciousness of the adversary. More concretely, we first propose an algorithm that enjoys $\widetilde{{O}}(\sqrt{T} + C^{\textsf{P}})$ regret where $C^{\textsf{P}}$ measures how adversarial the transition functions are and can be at most ${O}(T)$. While this algorithm itself requires knowledge of $C^{\textsf{P}}$, we further develop a black-box reduction approach that removes this requirement. Moreover, we also show that further refinements of the algorithm not only maintains the same regret bound, but also simultaneously adapts to easier environments (where losses are generated in a certain stochastically constrained manner as in Jin et al. [2021]) and achieves $\widetilde{{O}}(U + \sqrt{UC^{\textsf{L}}} + C^{\textsf{P}})$ regret, where $U$ is some standard gap-dependent coefficient and $C^{\textsf{L}}$ is the amount of corruption on losses.

A Near-Optimal Best-of-Both-Worlds Algorithm for Online Learning with Feedback Graphs

We consider online learning with feedback graphs, a sequential decision-making framework where the learner's feedback is determined by a directed graph over the action set. We present a computationally efficient algorithm for learning in this framework that simultaneously achieves near-optimal regret bounds in both stochastic and adversarial environments. The bound against oblivious adversaries is $\tilde{O} (\sqrt{\alpha T})$, where $T$ is the time horizon and $\alpha$ is the independence number of the feedback graph. The bound against stochastic environments is $O\big( (\ln T)^2 \max_{S\in \mathcal I(G)} \sum_{i \in S} \Delta_i^{-1}\big)$ where $\mathcal I(G)$ is the family of all independent sets in a suitably defined undirected version of the graph and $\Delta_i$ are the suboptimality gaps. The algorithm combines ideas from the EXP3++ algorithm for stochastic and adversarial bandits and the EXP3.G algorithm for feedback graphs with a novel exploration scheme. The scheme, which exploits the structure of the graph to reduce exploration, is key to obtain best-of-both-worlds guarantees with feedback graphs. We also extend our algorithm and results to a setting where the feedback graphs are allowed to change over time.

An Algorithm for Stochastic and Adversarial Bandits with Switching Costs

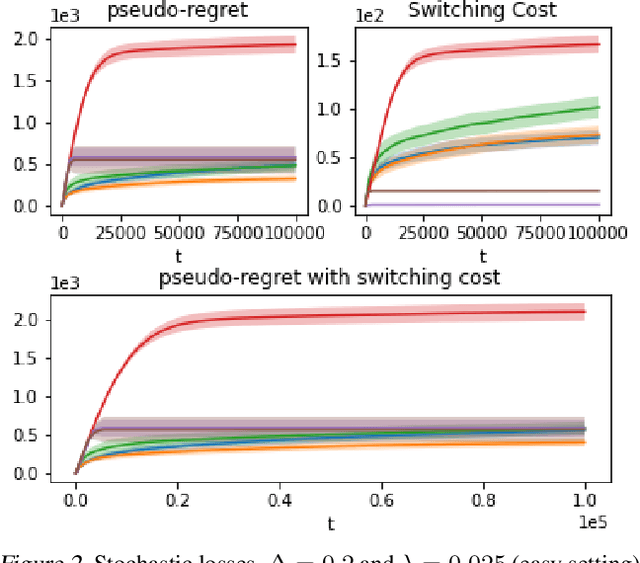
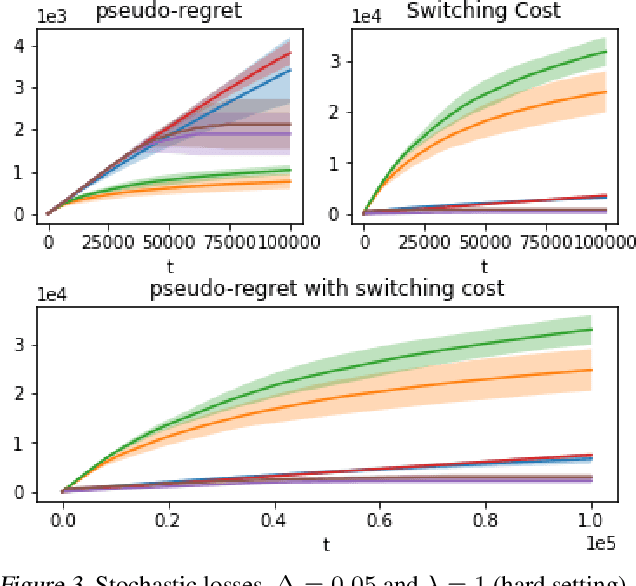
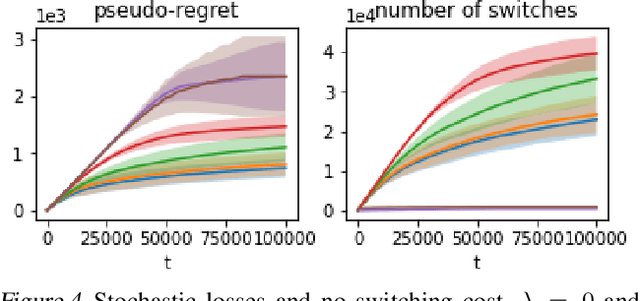
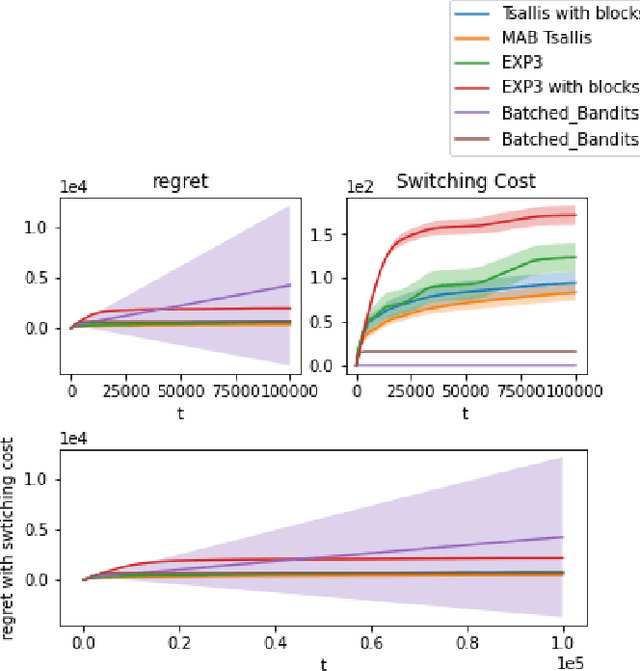
We propose an algorithm for stochastic and adversarial multiarmed bandits with switching costs, where the algorithm pays a price $\lambda$ every time it switches the arm being played. Our algorithm is based on adaptation of the Tsallis-INF algorithm of Zimmert and Seldin (2021) and requires no prior knowledge of the regime or time horizon. In the oblivious adversarial setting it achieves the minimax optimal regret bound of $O\big((\lambda K)^{1/3}T^{2/3} + \sqrt{KT}\big)$, where $T$ is the time horizon and $K$ is the number of arms. In the stochastically constrained adversarial regime, which includes the stochastic regime as a special case, it achieves a regret bound of $O\left(\big((\lambda K)^{2/3} T^{1/3} + \ln T\big)\sum_{i \neq i^*} \Delta_i^{-1}\right)$, where $\Delta_i$ are the suboptimality gaps and $i^*$ is a unique optimal arm. In the special case of $\lambda = 0$ (no switching costs), both bounds are minimax optimal within constants. We also explore variants of the problem, where switching cost is allowed to change over time. We provide experimental evaluation showing competitiveness of our algorithm with the relevant baselines in the stochastic, stochastically constrained adversarial, and adversarial regimes with fixed switching cost.