Achieving O(1/N) Optimality Gap in Restless Bandits through Diffusion Approximation

We study the finite horizon Restless Multi-Armed Bandit (RMAB) problem with $N$ homogeneous arms, focusing on the challenges posed by degenerate RMABs, which are prevalent in practical applications. While previous work has shown that Linear Programming (LP)-based policies achieve exponentially fast convergence relative to the LP upper bound in non-degenerate models, applying these LP-based policies to degenerate RMABs results in slower convergence rates of $O(1/\sqrt{N})$. We construct a diffusion system that incorporates both the mean and variance of the stochastic processes, in contrast to the fluid system from the LP, which only accounts for the mean, thereby providing a more accurate representation of RMAB dynamics. Consequently, our novel diffusion-resolving policy achieves an optimality gap of $O(1/N)$ relative to the true optimal value, rather than the LP upper bound, revealing that the fluid approximation and the LP upper bound are too loose in degenerate settings. These insights pave the way for constructing policies that surpass the $O(1/\sqrt{N})$ optimality gap for any RMAB, whether degenerate or not.

When is exponential asymptotic optimality achievable in average-reward restless bandits?

We consider the discrete-time infinite-horizon average-reward restless bandit problem. We propose a novel policy that maintains two dynamic subsets of arms: one subset of arms has a nearly optimal state distribution and takes actions according to an Optimal Local Control routine; the other subset of arms is driven towards the optimal state distribution and gradually merged into the first subset. We show that our policy is asymptotically optimal with an $O(\exp(-C N))$ optimality gap for an $N$-armed problem, under the mild assumptions of aperiodic-unichain, non-degeneracy, and local stability. Our policy is the first to achieve exponential asymptotic optimality under the above set of easy-to-verify assumptions, whereas prior work either requires a strong Global Attractor assumption or only achieves an $O(1/\sqrt{N})$ optimality gap. We further discuss the fundamental obstacles in significantly weakening our assumptions. In particular, we prove a lower bound showing that local stability is fundamental for exponential asymptotic optimality.

Unichain and Aperiodicity are Sufficient for Asymptotic Optimality of Average-Reward Restless Bandits

We consider the infinite-horizon, average-reward restless bandit problem in discrete time. We propose a new class of policies that are designed to drive a progressively larger subset of arms toward the optimal distribution. We show that our policies are asymptotically optimal with an $O(1/\sqrt{N})$ optimality gap for an $N$-armed problem, provided that the single-armed relaxed problem is unichain and aperiodic. Our approach departs from most existing work that focuses on index or priority policies, which rely on the Uniform Global Attractor Property (UGAP) to guarantee convergence to the optimum, or a recently developed simulation-based policy, which requires a Synchronization Assumption (SA).

Efficient Reinforcement Learning for Routing Jobs in Heterogeneous Queueing Systems

We consider the problem of efficiently routing jobs that arrive into a central queue to a system of heterogeneous servers. Unlike homogeneous systems, a threshold policy, that routes jobs to the slow server(s) when the queue length exceeds a certain threshold, is known to be optimal for the one-fast-one-slow two-server system. But an optimal policy for the multi-server system is unknown and non-trivial to find. While Reinforcement Learning (RL) has been recognized to have great potential for learning policies in such cases, our problem has an exponentially large state space size, rendering standard RL inefficient. In this work, we propose ACHQ, an efficient policy gradient based algorithm with a low dimensional soft threshold policy parameterization that leverages the underlying queueing structure. We provide stationary-point convergence guarantees for the general case and despite the low-dimensional parameterization prove that ACHQ converges to an approximate global optimum for the special case of two servers. Simulations demonstrate an improvement in expected response time of up to ~30% over the greedy policy that routes to the fastest available server.

Restless Bandits with Average Reward: Breaking the Uniform Global Attractor Assumption

We study the infinite-horizon restless bandit problem with the average reward criterion, under both discrete-time and continuous-time settings. A fundamental question is how to design computationally efficient policies that achieve a diminishing optimality gap as the number of arms, $N$, grows large. Existing results on asymptotical optimality all rely on the uniform global attractor property (UGAP), a complex and challenging-to-verify assumption. In this paper, we propose a general, simulation-based framework that converts any single-armed policy into a policy for the original $N$-armed problem. This is accomplished by simulating the single-armed policy on each arm and carefully steering the real state towards the simulated state. Our framework can be instantiated to produce a policy with an $O(1/\sqrt{N})$ optimality gap. In the discrete-time setting, our result holds under a simpler synchronization assumption, which covers some problem instances that do not satisfy UGAP. More notably, in the continuous-time setting, our result does not require any additional assumptions beyond the standard unichain condition. In both settings, we establish the first asymptotic optimality result that does not require UGAP.

Sample Efficient Reinforcement Learning in Mixed Systems through Augmented Samples and Its Applications to Queueing Networks

This paper considers a class of reinforcement learning problems, which involve systems with two types of states: stochastic and pseudo-stochastic. In such systems, stochastic states follow a stochastic transition kernel while the transitions of pseudo-stochastic states are deterministic given the stochastic states/transitions. We refer to such systems as mixed systems, which are widely used in various applications, including manufacturing systems, communication networks, and queueing networks. We propose a sample efficient RL method that accelerates learning by generating augmented data samples. The proposed algorithm is data-driven and learns the policy from data samples from both real and augmented samples. This method significantly improves learning by reducing the sample complexity such that the dataset only needs to have sufficient coverage of the stochastic states. We analyze the sample complexity of the proposed method under Fitted Q Iteration (FQI) and demonstrate that the optimality gap decreases as $\tilde{\mathcal{O}}(\sqrt{{1}/{n}}+\sqrt{{1}/{m}}),$ where $n$ is the number of real samples and $m$ is the number of augmented samples per real sample. It is important to note that without augmented samples, the optimality gap is $\tilde{\mathcal{O}}(1)$ due to insufficient data coverage of the pseudo-stochastic states. Our experimental results on multiple queueing network applications confirm that the proposed method indeed significantly accelerates learning in both deep Q-learning and deep policy gradient.

Job Dispatching Policies for Queueing Systems with Unknown Service Rates

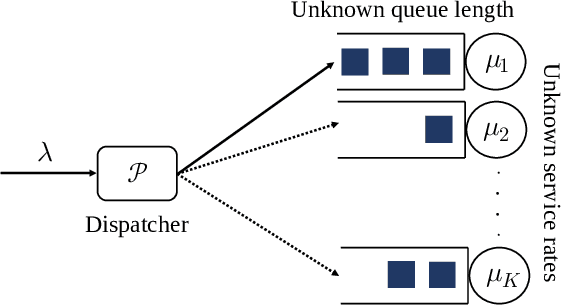
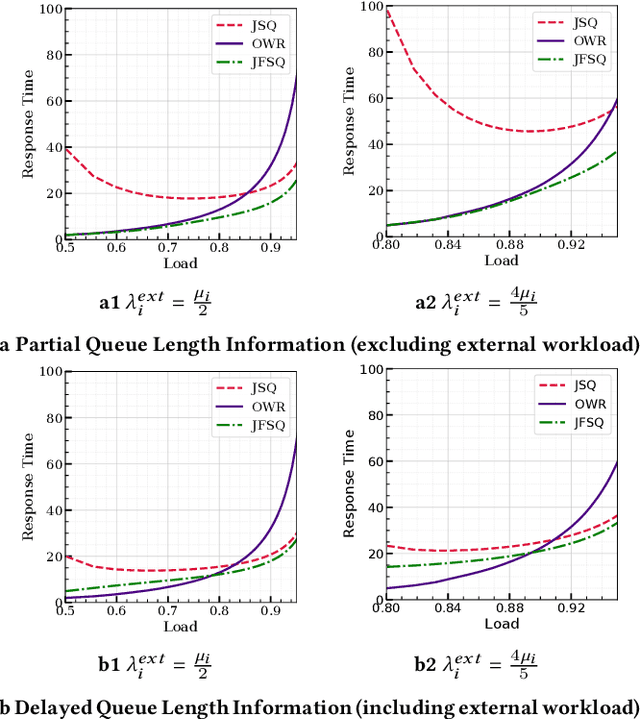
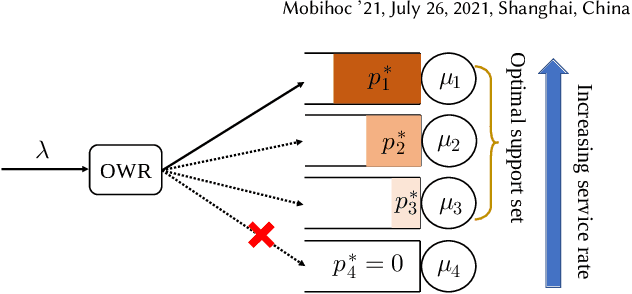
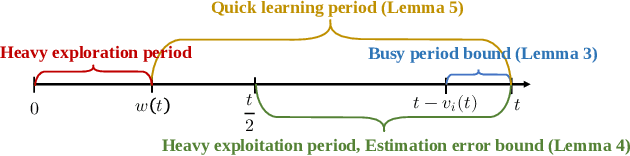
In multi-server queueing systems where there is no central queue holding all incoming jobs, job dispatching policies are used to assign incoming jobs to the queue at one of the servers. Classic job dispatching policies such as join-the-shortest-queue and shortest expected delay assume that the service rates and queue lengths of the servers are known to the dispatcher. In this work, we tackle the problem of job dispatching without the knowledge of service rates and queue lengths, where the dispatcher can only obtain noisy estimates of the service rates by observing job departures. This problem presents a novel exploration-exploitation trade-off between sending jobs to all the servers to estimate their service rates, and exploiting the currently known fastest servers to minimize the expected queueing delay. We propose a bandit-based exploration policy that learns the service rates from observed job departures. Unlike the standard multi-armed bandit problem where only one out of a finite set of actions is optimal, here the optimal policy requires identifying the optimal fraction of incoming jobs to be sent to each server. We present a regret analysis and simulations to demonstrate the effectiveness of the proposed bandit-based exploration policy.

On the Privacy-Utility Tradeoff in Peer-Review Data Analysis

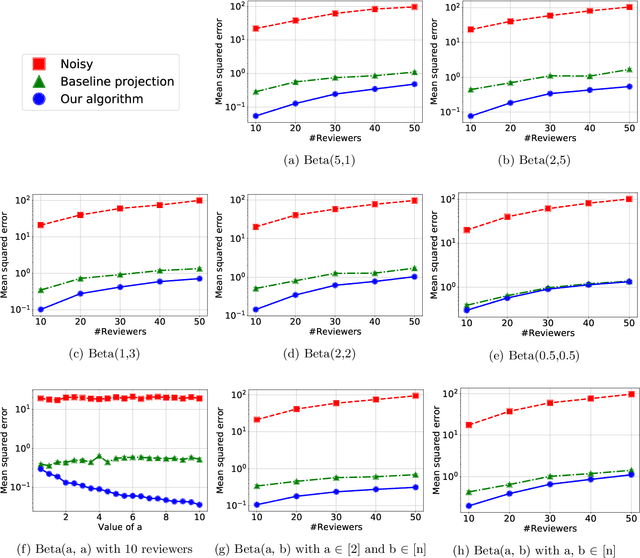
A major impediment to research on improving peer review is the unavailability of peer-review data, since any release of such data must grapple with the sensitivity of the peer review data in terms of protecting identities of reviewers from authors. We posit the need to develop techniques to release peer-review data in a privacy-preserving manner. Identifying this problem, in this paper we propose a framework for privacy-preserving release of certain conference peer-review data -- distributions of ratings, miscalibration, and subjectivity -- with an emphasis on the accuracy (or utility) of the released data. The crux of the framework lies in recognizing that a part of the data pertaining to the reviews is already available in public, and we use this information to post-process the data released by any privacy mechanism in a manner that improves the accuracy (utility) of the data while retaining the privacy guarantees. Our framework works with any privacy-preserving mechanism that operates via releasing perturbed data. We present several positive and negative theoretical results, including a polynomial-time algorithm for improving on the privacy-utility tradeoff.

QuickStop: A Markov Optimal Stopping Approach for Quickest Misinformation Detection

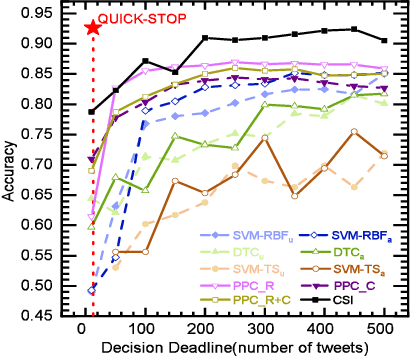
This paper combines data-driven and model-driven methods for real-time misinformation detection. Our algorithm, named QuickStop, is an optimal stopping algorithm based on a probabilistic information spreading model obtained from labeled data. The algorithm consists of an offline machine learning algorithm for learning the probabilistic information spreading model and an online optimal stopping algorithm to detect misinformation. The online detection algorithm has both low computational and memory complexities. Our numerical evaluations with a real-world dataset show that QuickStop outperforms existing misinformation detection algorithms in terms of both accuracy and detection time (number of observations needed for detection). Our evaluations with synthetic data further show that QuickStop is robust to (offline) learning errors.

Almost Boltzmann Exploration

Boltzmann exploration is widely used in reinforcement learning to provide a trade-off between exploration and exploitation. Recently, in (Cesa-Bianchi et al., 2017) it has been shown that pure Boltzmann exploration does not perform well from a regret perspective, even in the simplest setting of stochastic multi-armed bandit (MAB) problems. In this paper, we show that a simple modification to Boltzmann exploration, motivated by a variation of the standard doubling trick, achieves $O(K\log^{1+\alpha} T)$ regret for a stochastic MAB problem with $K$ arms, where $\alpha>0$ is a parameter of the algorithm. This improves on the result in (Cesa-Bianchi et al., 2017), where an algorithm inspired by the Gumbel-softmax trick achieves $O(K\log^2 T)$ regret. We also show that our algorithm achieves $O(\beta(G) \log^{1+\alpha} T)$ regret in stochastic MAB problems with graph-structured feedback, without knowledge of the graph structure, where $\beta(G)$ is the independence number of the feedback graph. Additionally, we present extensive experimental results on real datasets and applications for multi-armed bandits with both traditional bandit feedback and graph-structured feedback. In all cases, our algorithm performs as well or better than the state-of-the-art.