Job Dispatching Policies for Queueing Systems with Unknown Service Rates

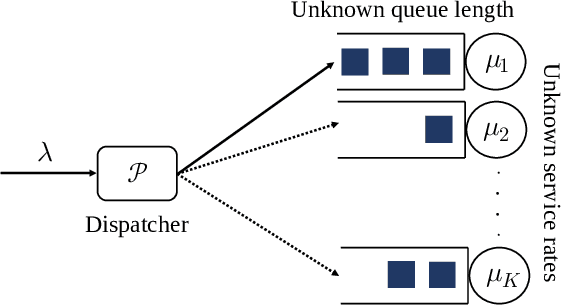
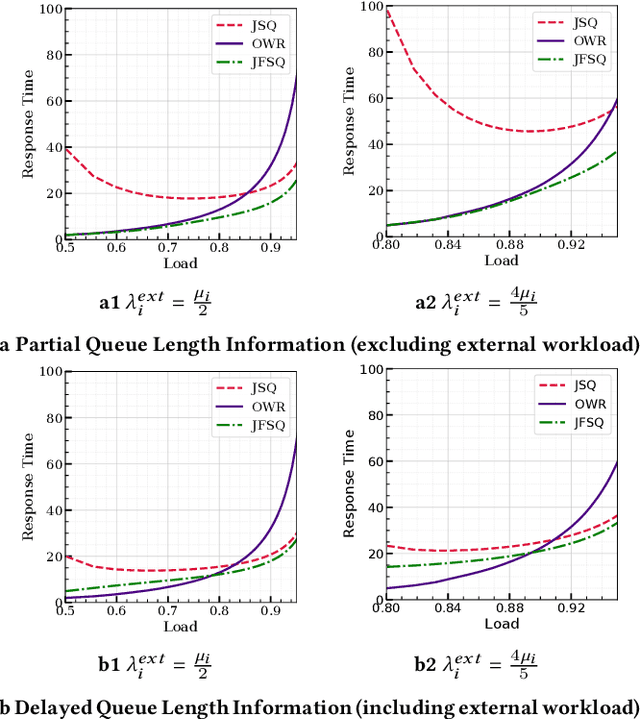
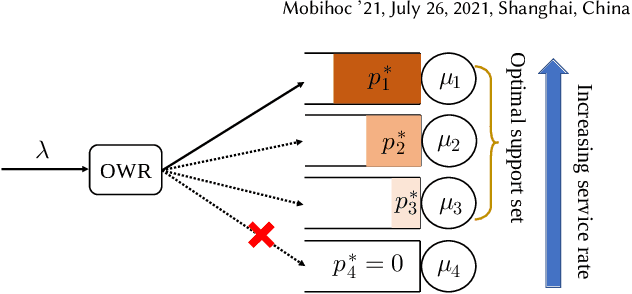
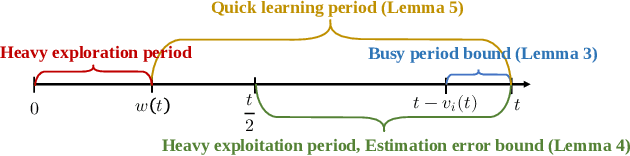
In multi-server queueing systems where there is no central queue holding all incoming jobs, job dispatching policies are used to assign incoming jobs to the queue at one of the servers. Classic job dispatching policies such as join-the-shortest-queue and shortest expected delay assume that the service rates and queue lengths of the servers are known to the dispatcher. In this work, we tackle the problem of job dispatching without the knowledge of service rates and queue lengths, where the dispatcher can only obtain noisy estimates of the service rates by observing job departures. This problem presents a novel exploration-exploitation trade-off between sending jobs to all the servers to estimate their service rates, and exploiting the currently known fastest servers to minimize the expected queueing delay. We propose a bandit-based exploration policy that learns the service rates from observed job departures. Unlike the standard multi-armed bandit problem where only one out of a finite set of actions is optimal, here the optimal policy requires identifying the optimal fraction of incoming jobs to be sent to each server. We present a regret analysis and simulations to demonstrate the effectiveness of the proposed bandit-based exploration policy.

Sequential Mode Estimation with Oracle Queries

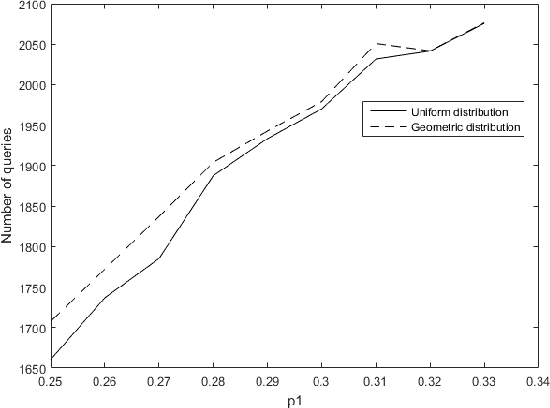
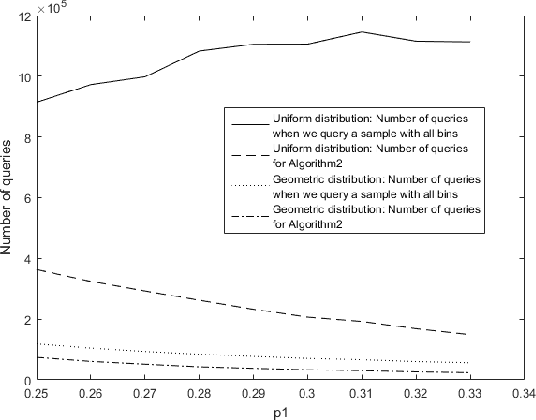
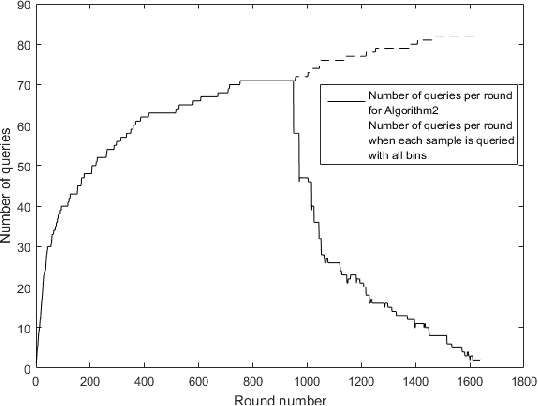
We consider the problem of adaptively PAC-learning a probability distribution $\mathcal{P}$'s mode by querying an oracle for information about a sequence of i.i.d. samples $X_1, X_2, \ldots$ generated from $\mathcal{P}$. We consider two different query models: (a) each query is an index $i$ for which the oracle reveals the value of the sample $X_i$, (b) each query is comprised of two indices $i$ and $j$ for which the oracle reveals if the samples $X_i$ and $X_j$ are the same or not. For these query models, we give sequential mode-estimation algorithms which, at each time $t$, either make a query to the corresponding oracle based on past observations, or decide to stop and output an estimate for the distribution's mode, required to be correct with a specified confidence. We analyze the query complexity of these algorithms for any underlying distribution $\mathcal{P}$, and derive corresponding lower bounds on the optimal query complexity under the two querying models.