Online Statistical Inference of Constrained Stochastic Optimization via Random Scaling

Constrained stochastic nonlinear optimization problems have attracted significant attention for their ability to model complex real-world scenarios in physics, economics, and biology. As datasets continue to grow, online inference methods have become crucial for enabling real-time decision-making without the need to store historical data. In this work, we develop an online inference procedure for constrained stochastic optimization by leveraging a method called Sketched Stochastic Sequential Quadratic Programming (SSQP). As a direct generalization of sketched Newton methods, SSQP approximates the objective with a quadratic model and the constraints with a linear model at each step, then applies a sketching solver to inexactly solve the resulting subproblem. Building on this design, we propose a new online inference procedure called random scaling. In particular, we construct a test statistic based on SSQP iterates whose limiting distribution is free of any unknown parameters. Compared to existing online inference procedures, our approach offers two key advantages: (i) it enables the construction of asymptotically valid confidence intervals; and (ii) it is matrix-free, i.e. the computation involves only primal-dual SSQP iterates $(\boldsymbol{x}_t, \boldsymbol{\lambda}_t)$ without requiring any matrix inversions. We validate our theory through numerical experiments on nonlinearly constrained regression problems and demonstrate the superior performance of our random scaling method over existing inference procedures.

Smoothed SGD for quantiles: Bahadur representation and Gaussian approximation

This paper considers the estimation of quantiles via a smoothed version of the stochastic gradient descent (SGD) algorithm. By smoothing the score function in the conventional SGD quantile algorithm, we achieve monotonicity in the quantile level in that the estimated quantile curves do not cross. We derive non-asymptotic tail probability bounds for the smoothed SGD quantile estimate both for the case with and without Polyak-Ruppert averaging. For the latter, we also provide a uniform Bahadur representation and a resulting Gaussian approximation result. Numerical studies show good finite sample behavior for our theoretical results.

Sharp Gaussian approximations for Decentralized Federated Learning

Federated Learning has gained traction in privacy-sensitive collaborative environments, with local SGD emerging as a key optimization method in decentralized settings. While its convergence properties are well-studied, asymptotic statistical guarantees beyond convergence remain limited. In this paper, we present two generalized Gaussian approximation results for local SGD and explore their implications. First, we prove a Berry-Esseen theorem for the final local SGD iterates, enabling valid multiplier bootstrap procedures. Second, motivated by robustness considerations, we introduce two distinct time-uniform Gaussian approximations for the entire trajectory of local SGD. The time-uniform approximations support Gaussian bootstrap-based tests for detecting adversarial attacks. Extensive simulations are provided to support our theoretical results.

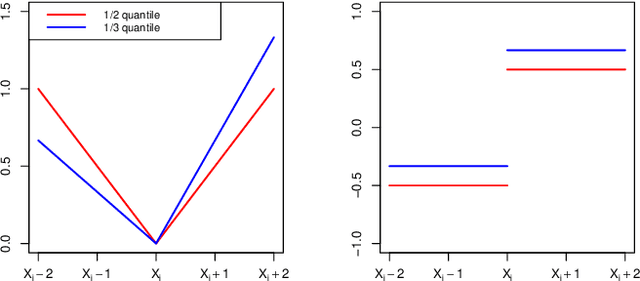
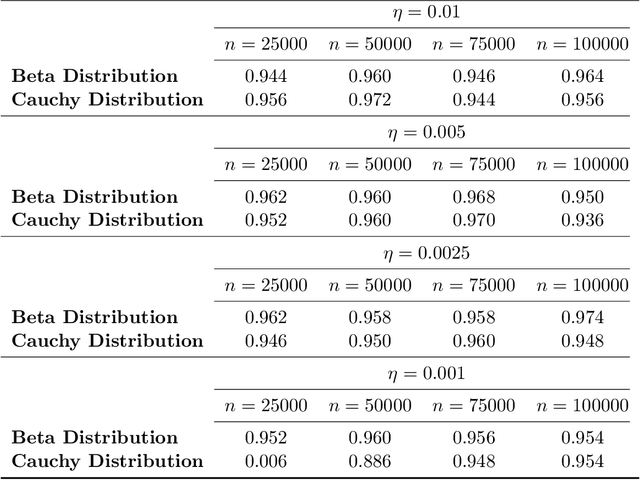
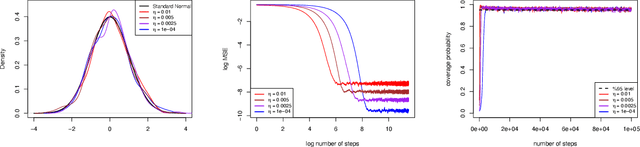
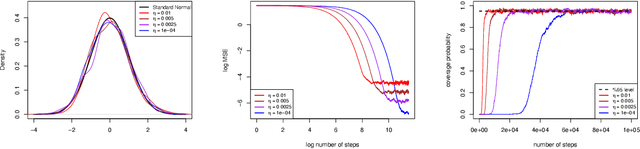
Online Inference for Quantiles by Constant Learning-Rate Stochastic Gradient Descent

This paper proposes an online inference method of the stochastic gradient descent (SGD) with a constant learning rate for quantile loss functions with theoretical guarantees. Since the quantile loss function is neither smooth nor strongly convex, we view such SGD iterates as an irreducible and positive recurrent Markov chain. By leveraging this interpretation, we show the existence of a unique asymptotic stationary distribution, regardless of the arbitrarily fixed initialization. To characterize the exact form of this limiting distribution, we derive bounds for its moment generating function and tail probabilities, controlling over the first and second moments of SGD iterates. By these techniques, we prove that the stationary distribution converges to a Gaussian distribution as the constant learning rate $\eta\rightarrow0$. Our findings provide the first central limit theorem (CLT)-type theoretical guarantees for the last iterate of constant learning-rate SGD in non-smooth and non-strongly convex settings. We further propose a recursive algorithm to construct confidence intervals of SGD iterates in an online manner. Numerical studies demonstrate strong finite-sample performance of our proposed quantile estimator and inference method. The theoretical tools in this study are of independent interest to investigate general transition kernels in Markov chains.

Asymptotics of Stochastic Gradient Descent with Dropout Regularization in Linear Models

This paper proposes an asymptotic theory for online inference of the stochastic gradient descent (SGD) iterates with dropout regularization in linear regression. Specifically, we establish the geometric-moment contraction (GMC) for constant step-size SGD dropout iterates to show the existence of a unique stationary distribution of the dropout recursive function. By the GMC property, we provide quenched central limit theorems (CLT) for the difference between dropout and $\ell^2$-regularized iterates, regardless of initialization. The CLT for the difference between the Ruppert-Polyak averaged SGD (ASGD) with dropout and $\ell^2$-regularized iterates is also presented. Based on these asymptotic normality results, we further introduce an online estimator for the long-run covariance matrix of ASGD dropout to facilitate inference in a recursive manner with efficiency in computational time and memory. The numerical experiments demonstrate that for sufficiently large samples, the proposed confidence intervals for ASGD with dropout nearly achieve the nominal coverage probability.

High Confidence Level Inference is Almost Free using Parallel Stochastic Optimization

Uncertainty quantification for estimation through stochastic optimization solutions in an online setting has gained popularity recently. This paper introduces a novel inference method focused on constructing confidence intervals with efficient computation and fast convergence to the nominal level. Specifically, we propose to use a small number of independent multi-runs to acquire distribution information and construct a t-based confidence interval. Our method requires minimal additional computation and memory beyond the standard updating of estimates, making the inference process almost cost-free. We provide a rigorous theoretical guarantee for the confidence interval, demonstrating that the coverage is approximately exact with an explicit convergence rate and allowing for high confidence level inference. In particular, a new Gaussian approximation result is developed for the online estimators to characterize the coverage properties of our confidence intervals in terms of relative errors. Additionally, our method also allows for leveraging parallel computing to further accelerate calculations using multiple cores. It is easy to implement and can be integrated with existing stochastic algorithms without the need for complicated modifications.

Weighted Averaged Stochastic Gradient Descent: Asymptotic Normality and Optimality

Stochastic Gradient Descent (SGD) is one of the simplest and most popular algorithms in modern statistical and machine learning due to its computational and memory efficiency. Various averaging schemes have been proposed to accelerate the convergence of SGD in different settings. In this paper, we explore a general averaging scheme for SGD. Specifically, we establish the asymptotic normality of a broad range of weighted averaged SGD solutions and provide asymptotically valid online inference approaches. Furthermore, we propose an adaptive averaging scheme that exhibits both optimal statistical rate and favorable non-asymptotic convergence, drawing insights from the optimal weight for the linear model in terms of non-asymptotic mean squared error (MSE).

Explainable AI for a No-Teardown Vehicle Component Cost Estimation: A Top-Down Approach

The broader ambition of this article is to popularize an approach for the fair distribution of the quantity of a system's output to its subsystems, while allowing for underlying complex subsystem level interactions. Particularly, we present a data-driven approach to vehicle price modeling and its component price estimation by leveraging a combination of concepts from machine learning and game theory. We show an alternative to common teardown methodologies and surveying approaches for component and vehicle price estimation at the manufacturer's suggested retail price (MSRP) level that has the advantage of bypassing the uncertainties involved in 1) the gathering of teardown data, 2) the need to perform expensive and biased surveying, and 3) the need to perform retail price equivalent (RPE) or indirect cost multiplier (ICM) adjustments to mark up direct manufacturing costs to MSRP. This novel exercise not only provides accurate pricing of the technologies at the customer level, but also shows the, a priori known, large gaps in pricing strategies between manufacturers, vehicle sizes, classes, market segments, and other factors. There is also clear synergism or interaction between the price of certain technologies and other specifications present in the same vehicle. Those (unsurprising) results are indication that old methods of manufacturer-level component costing, aggregation, and the application of a flat and rigid RPE or ICM adjustment factor should be carefully examined. The findings are based on an extensive database, developed by Argonne National Laboratory, that includes more than 64,000 vehicles covering MY1990 to MY2020 over hundreds of vehicle specs.

A Fully Online Approach for Covariance Matrices Estimation of Stochastic Gradient Descent Solutions

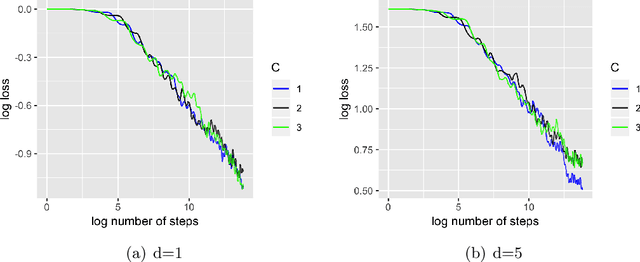
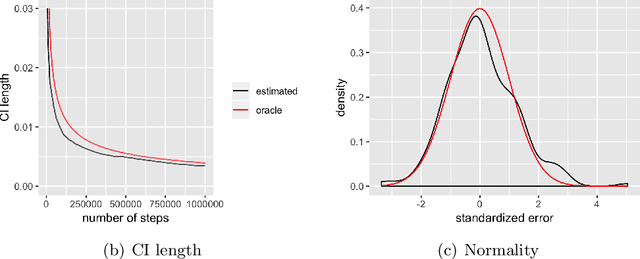
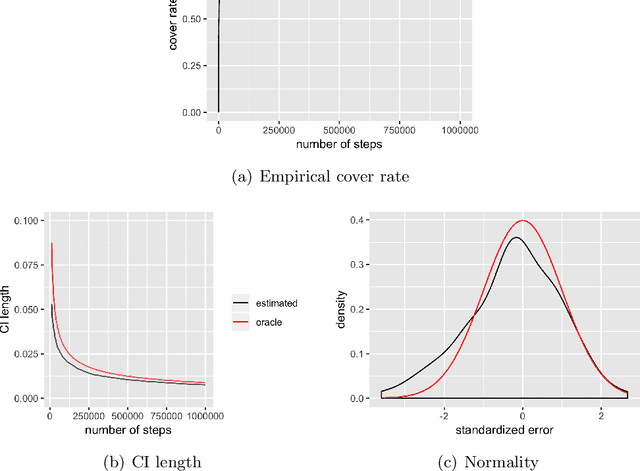
Stochastic gradient descent (SGD) algorithm is widely used for parameter estimation especially in online setting. While this recursive algorithm is popular for computation and memory efficiency, the problem of quantifying variability and randomness of the solutions has been rarely studied. This paper aims at conducting statistical inference of SGD-based estimates in online setting. In particular, we propose a fully online estimator for the covariance matrix of averaged SGD iterates (ASGD). Based on the classic asymptotic normality results of ASGD, we construct asymptotically valid confidence intervals for model parameters. Upon receiving new observations, we can quickly update the covariance estimator and confidence intervals. This approach fits in online setting even if the total number of data is unknown and takes the full advantage of SGD: efficiency in both computation and memory.