Online Statistical Inference of Constrained Stochastic Optimization via Random Scaling

Constrained stochastic nonlinear optimization problems have attracted significant attention for their ability to model complex real-world scenarios in physics, economics, and biology. As datasets continue to grow, online inference methods have become crucial for enabling real-time decision-making without the need to store historical data. In this work, we develop an online inference procedure for constrained stochastic optimization by leveraging a method called Sketched Stochastic Sequential Quadratic Programming (SSQP). As a direct generalization of sketched Newton methods, SSQP approximates the objective with a quadratic model and the constraints with a linear model at each step, then applies a sketching solver to inexactly solve the resulting subproblem. Building on this design, we propose a new online inference procedure called random scaling. In particular, we construct a test statistic based on SSQP iterates whose limiting distribution is free of any unknown parameters. Compared to existing online inference procedures, our approach offers two key advantages: (i) it enables the construction of asymptotically valid confidence intervals; and (ii) it is matrix-free, i.e. the computation involves only primal-dual SSQP iterates $(\boldsymbol{x}_t, \boldsymbol{\lambda}_t)$ without requiring any matrix inversions. We validate our theory through numerical experiments on nonlinearly constrained regression problems and demonstrate the superior performance of our random scaling method over existing inference procedures.

High Probability Complexity Bounds of Trust-Region Stochastic Sequential Quadratic Programming with Heavy-Tailed Noise

In this paper, we consider nonlinear optimization problems with a stochastic objective and deterministic equality constraints. We propose a Trust-Region Stochastic Sequential Quadratic Programming (TR-SSQP) method and establish its high-probability iteration complexity bounds for identifying first- and second-order $\epsilon$-stationary points. In our algorithm, we assume that exact objective values, gradients, and Hessians are not directly accessible but can be estimated via zeroth-, first-, and second-order probabilistic oracles. Compared to existing complexity studies of SSQP methods that rely on a zeroth-order oracle with sub-exponential tail noise (i.e., light-tailed) and focus mostly on first-order stationarity, our analysis accommodates irreducible and heavy-tailed noise in the zeroth-order oracle and significantly extends the analysis to second-order stationarity. We show that under weaker noise conditions, our method achieves the same high-probability first-order iteration complexity bounds, while also exhibiting promising second-order iteration complexity bounds. Specifically, the method identifies a first-order $\epsilon$-stationary point in $\mathcal{O}(\epsilon^{-2})$ iterations and a second-order $\epsilon$-stationary point in $\mathcal{O}(\epsilon^{-3})$ iterations with high probability, provided that $\epsilon$ is lower bounded by a constant determined by the irreducible noise level in estimation. We validate our theoretical findings and evaluate the practical performance of our method on CUTEst benchmark test set.

Online Covariance Matrix Estimation in Sketched Newton Methods

Given the ubiquity of streaming data, online algorithms have been widely used for parameter estimation, with second-order methods particularly standing out for their efficiency and robustness. In this paper, we study an online sketched Newton method that leverages a randomized sketching technique to perform an approximate Newton step in each iteration, thereby eliminating the computational bottleneck of second-order methods. While existing studies have established the asymptotic normality of sketched Newton methods, a consistent estimator of the limiting covariance matrix remains an open problem. We propose a fully online covariance matrix estimator that is constructed entirely from the Newton iterates and requires no matrix factorization. Compared to covariance estimators for first-order online methods, our estimator for second-order methods is batch-free. We establish the consistency and convergence rate of our estimator, and coupled with asymptotic normality results, we can then perform online statistical inference for the model parameters based on sketched Newton methods. We also discuss the extension of our estimator to constrained problems, and demonstrate its superior performance on regression problems as well as benchmark problems in the CUTEst set.

Online Covariance Estimation in Nonsmooth Stochastic Approximation

We consider applying stochastic approximation (SA) methods to solve nonsmooth variational inclusion problems. Existing studies have shown that the averaged iterates of SA methods exhibit asymptotic normality, with an optimal limiting covariance matrix in the local minimax sense of H\'ajek and Le Cam. However, no methods have been proposed to estimate this covariance matrix in a nonsmooth and potentially non-monotone (nonconvex) setting. In this paper, we study an online batch-means covariance matrix estimator introduced in Zhu et al.(2023). The estimator groups the SA iterates appropriately and computes the sample covariance among batches as an estimate of the limiting covariance. Its construction does not require prior knowledge of the total sample size, and updates can be performed recursively as new data arrives. We establish that, as long as the batch size sequence is properly specified (depending on the stepsize sequence), the estimator achieves a convergence rate of order $O(\sqrt{d}n^{-1/8+\varepsilon})$ for any $\varepsilon>0$, where $d$ and $n$ denote the problem dimensionality and the number of iterations (or samples) used. Although the problem is nonsmooth and potentially non-monotone (nonconvex), our convergence rate matches the best-known rate for covariance estimation methods using only first-order information in smooth and strongly-convex settings. The consistency of this covariance estimator enables asymptotically valid statistical inference, including constructing confidence intervals and performing hypothesis testing.

Physics-Informed Neural Networks with Trust-Region Sequential Quadratic Programming

Physics-Informed Neural Networks (PINNs) represent a significant advancement in Scientific Machine Learning (SciML), which integrate physical domain knowledge into an empirical loss function as soft constraints and apply existing machine learning methods to train the model. However, recent research has noted that PINNs may fail to learn relatively complex Partial Differential Equations (PDEs). This paper addresses the failure modes of PINNs by introducing a novel, hard-constrained deep learning method -- trust-region Sequential Quadratic Programming (trSQP-PINN). In contrast to directly training the penalized soft-constrained loss as in PINNs, our method performs a linear-quadratic approximation of the hard-constrained loss, while leveraging the soft-constrained loss to adaptively adjust the trust-region radius. We only trust our model approximations and make updates within the trust region, and such an updating manner can overcome the ill-conditioning issue of PINNs. We also address the computational bottleneck of second-order SQP methods by employing quasi-Newton updates for second-order information, and importantly, we introduce a simple pretraining step to further enhance training efficiency of our method. We demonstrate the effectiveness of trSQP-PINN through extensive experiments. Compared to existing hard-constrained methods for PINNs, such as penalty methods and augmented Lagrangian methods, trSQP-PINN significantly improves the accuracy of the learned PDE solutions, achieving up to 1-3 orders of magnitude lower errors. Additionally, our pretraining step is generally effective for other hard-constrained methods, and experiments have shown the robustness of our method against both problem-specific parameters and algorithm tuning parameters.

Constrained Optimization via Exact Augmented Lagrangian and Randomized Iterative Sketching

We consider solving equality-constrained nonlinear, nonconvex optimization problems. This class of problems appears widely in a variety of applications in machine learning and engineering, ranging from constrained deep neural networks, to optimal control, to PDE-constrained optimization. We develop an adaptive inexact Newton method for this problem class. In each iteration, we solve the Lagrangian Newton system inexactly via a randomized iterative sketching solver, and select a suitable stepsize by performing line search on an exact augmented Lagrangian merit function. The randomized solvers have advantages over deterministic linear system solvers by significantly reducing per-iteration flops complexity and storage cost, when equipped with suitable sketching matrices. Our method adaptively controls the accuracy of the randomized solver and the penalty parameters of the exact augmented Lagrangian, to ensure that the inexact Newton direction is a descent direction of the exact augmented Lagrangian. This allows us to establish a global almost sure convergence. We also show that a unit stepsize is admissible locally, so that our method exhibits a local linear convergence. Furthermore, we prove that the linear convergence can be strengthened to superlinear convergence if we gradually sharpen the adaptive accuracy condition on the randomized solver. We demonstrate the superior performance of our method on benchmark nonlinear problems in CUTEst test set, constrained logistic regression with data from LIBSVM, and a PDE-constrained problem.

Fully Stochastic Trust-Region Sequential Quadratic Programming for Equality-Constrained Optimization Problems

We propose a trust-region stochastic sequential quadratic programming algorithm (TR-StoSQP) to solve nonlinear optimization problems with stochastic objectives and deterministic equality constraints. We consider a fully stochastic setting, where in each iteration a single sample is generated to estimate the objective gradient. The algorithm adaptively selects the trust-region radius and, compared to the existing line-search StoSQP schemes, allows us to employ indefinite Hessian matrices (i.e., Hessians without modification) in SQP subproblems. As a trust-region method for constrained optimization, our algorithm needs to address an infeasibility issue -- the linearized equality constraints and trust-region constraints might lead to infeasible SQP subproblems. In this regard, we propose an \textit{adaptive relaxation technique} to compute the trial step that consists of a normal step and a tangential step. To control the lengths of the two steps, we adaptively decompose the trust-region radius into two segments based on the proportions of the feasibility and optimality residuals to the full KKT residual. The normal step has a closed form, while the tangential step is solved from a trust-region subproblem, to which a solution ensuring the Cauchy reduction is sufficient for our study. We establish the global almost sure convergence guarantee for TR-StoSQP, and illustrate its empirical performance on both a subset of problems in the CUTEst test set and constrained logistic regression problems using data from the LIBSVM collection.

Asymptotic Convergence Rate and Statistical Inference for Stochastic Sequential Quadratic Programming

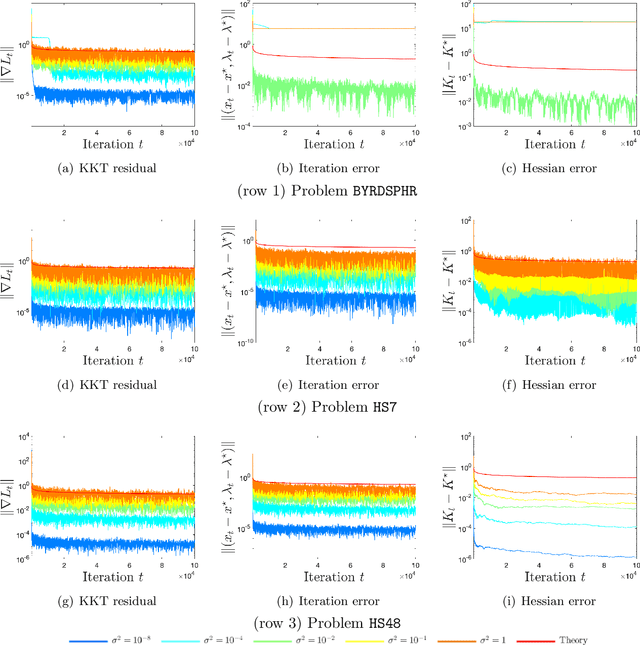
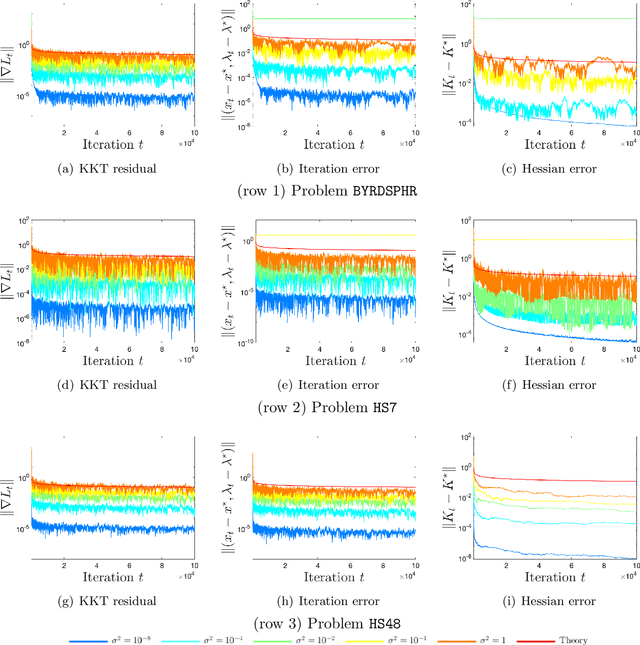
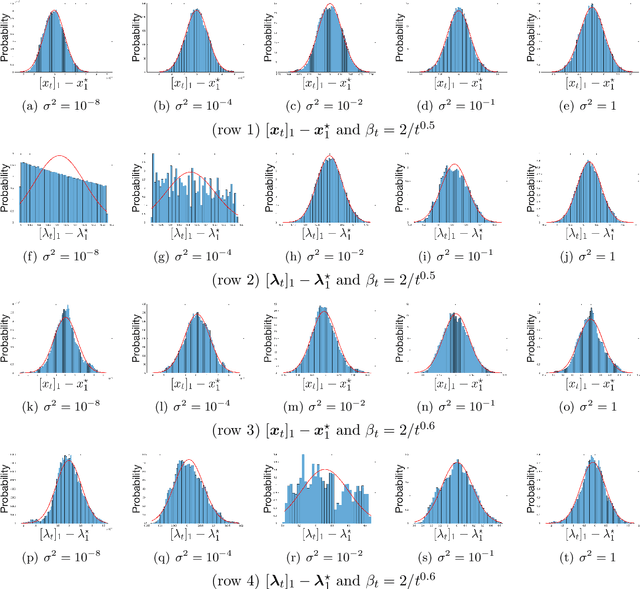
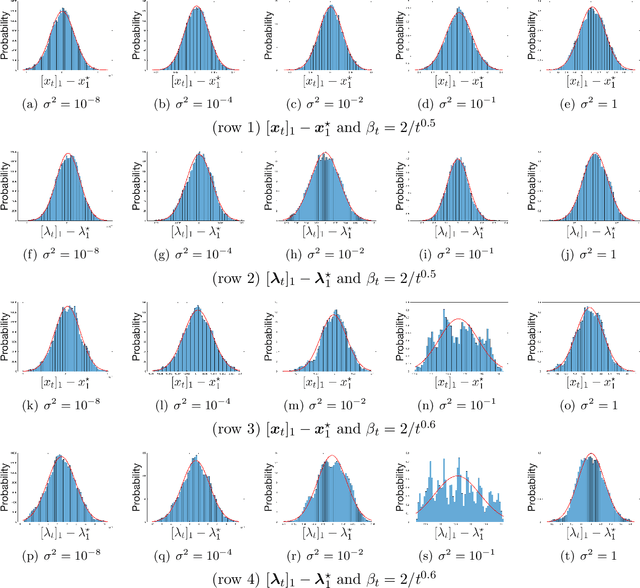
We apply a stochastic sequential quadratic programming (StoSQP) algorithm to solve constrained nonlinear optimization problems, where the objective is stochastic and the constraints are deterministic. We study a fully stochastic setup, where only a single sample is available in each iteration for estimating the gradient and Hessian of the objective. We allow StoSQP to select a random stepsize $\bar{\alpha}_t$ adaptively, such that $\beta_t\leq \bar{\alpha}_t \leq \beta_t+\chi_t$, where $\beta_t$, $\chi_t=o(\beta_t)$ are prespecified deterministic sequences. We also allow StoSQP to solve Newton system inexactly via randomized iterative solvers, e.g., with the sketch-and-project method; and we do not require the approximation error of inexact Newton direction to vanish. For this general StoSQP framework, we establish the asymptotic convergence rate for its last iterate, with the worst-case iteration complexity as a byproduct; and we perform statistical inference. In particular, with proper decaying $\beta_t,\chi_t$, we show that: (i) the StoSQP scheme can take at most $O(1/\epsilon^4)$ iterations to achieve $\epsilon$-stationarity; (ii) asymptotically and almost surely, $\|(x_t -x^\star, \lambda_t - \lambda^\star)\| = O(\sqrt{\beta_t\log(1/\beta_t)})+O(\chi_t/\beta_t)$, where $(x_t,\lambda_t)$ is the primal-dual StoSQP iterate; (iii) the sequence $1/\sqrt{\beta_t}\cdot (x_t -x^\star, \lambda_t - \lambda^\star)$ converges to a mean zero Gaussian distribution with a nontrivial covariance matrix. Moreover, we establish the Berry-Esseen bound for $(x_t, \lambda_t)$ to measure quantitatively the convergence of its distribution function. We also provide a practical estimator for the covariance matrix, from which the confidence intervals of $(x^\star, \lambda^\star)$ can be constructed using iterates $\{(x_t,\lambda_t)\}_t$. Our theorems are validated using nonlinear problems in CUTEst test set.

Hessian Averaging in Stochastic Newton Methods Achieves Superlinear Convergence

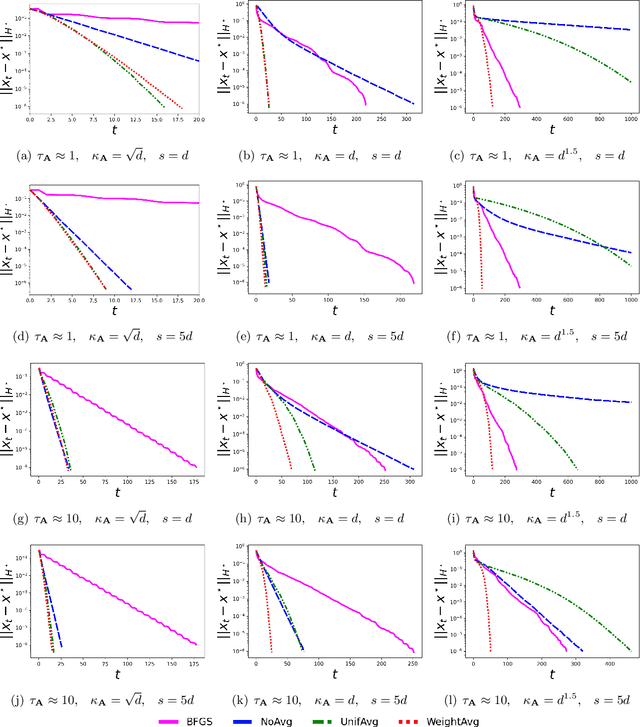
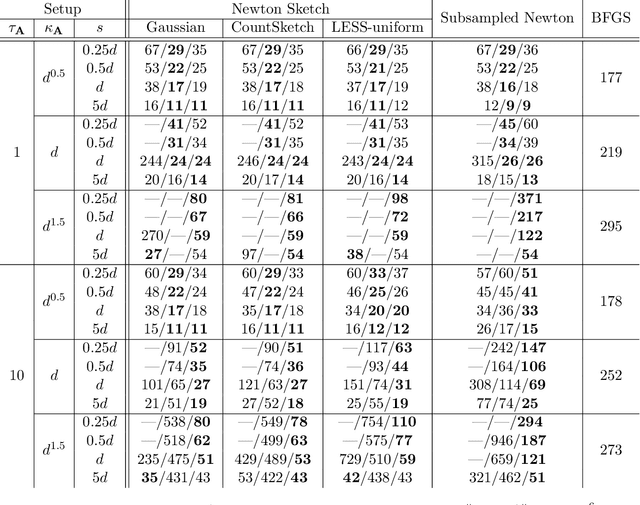
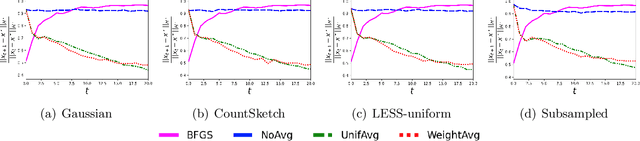
We consider minimizing a smooth and strongly convex objective function using a stochastic Newton method. At each iteration, the algorithm is given an oracle access to a stochastic estimate of the Hessian matrix. The oracle model includes popular algorithms such as the Subsampled Newton and Newton Sketch, which can efficiently construct stochastic Hessian estimates for many tasks. Despite using second-order information, these existing methods do not exhibit superlinear convergence, unless the stochastic noise is gradually reduced to zero during the iteration, which would lead to a computational blow-up in the per-iteration cost. We address this limitation with Hessian averaging: instead of using the most recent Hessian estimate, our algorithm maintains an average of all past estimates. This reduces the stochastic noise while avoiding the computational blow-up. We show that this scheme enjoys local $Q$-superlinear convergence with a non-asymptotic rate of $(\Upsilon\sqrt{\log (t)/t}\,)^{t}$, where $\Upsilon$ is proportional to the level of stochastic noise in the Hessian oracle. A potential drawback of this (uniform averaging) approach is that the averaged estimates contain Hessian information from the global phase of the iteration, i.e., before the iterates converge to a local neighborhood. This leads to a distortion that may substantially delay the superlinear convergence until long after the local neighborhood is reached. To address this drawback, we study a number of weighted averaging schemes that assign larger weights to recent Hessians, so that the superlinear convergence arises sooner, albeit with a slightly slower rate. Remarkably, we show that there exists a universal weighted averaging scheme that transitions to local convergence at an optimal stage, and still enjoys a superlinear convergence~rate nearly (up to a logarithmic factor) matching that of uniform Hessian averaging.

Inequality Constrained Stochastic Nonlinear Optimization via Active-Set Sequential Quadratic Programming

We study nonlinear optimization problems with stochastic objective and deterministic equality and inequality constraints, which emerge in numerous applications including finance, manufacturing, power systems and, recently, deep neural networks. We propose an active-set stochastic sequential quadratic programming algorithm, using a differentiable exact augmented Lagrangian as the merit function. The algorithm adaptively selects the penalty parameters of augmented Lagrangian and performs stochastic line search to decide the stepsize. The global convergence is established: for any initialization, the "liminf" of the KKT residuals converges to zero almost surely. Our algorithm and analysis further develop the prior work \cite{Na2021Adaptive} by allowing nonlinear inequality constraints. We demonstrate the performance of the algorithm on a subset of nonlinear problems collected in the CUTEst test set.