Smoothed SGD for quantiles: Bahadur representation and Gaussian approximation

This paper considers the estimation of quantiles via a smoothed version of the stochastic gradient descent (SGD) algorithm. By smoothing the score function in the conventional SGD quantile algorithm, we achieve monotonicity in the quantile level in that the estimated quantile curves do not cross. We derive non-asymptotic tail probability bounds for the smoothed SGD quantile estimate both for the case with and without Polyak-Ruppert averaging. For the latter, we also provide a uniform Bahadur representation and a resulting Gaussian approximation result. Numerical studies show good finite sample behavior for our theoretical results.

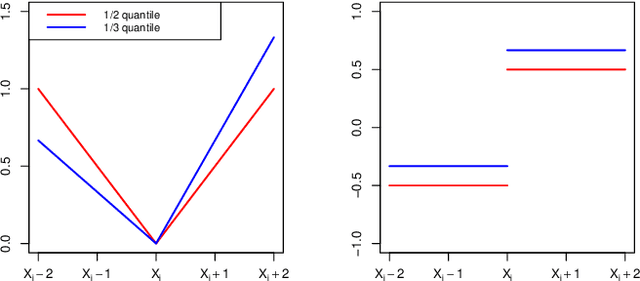
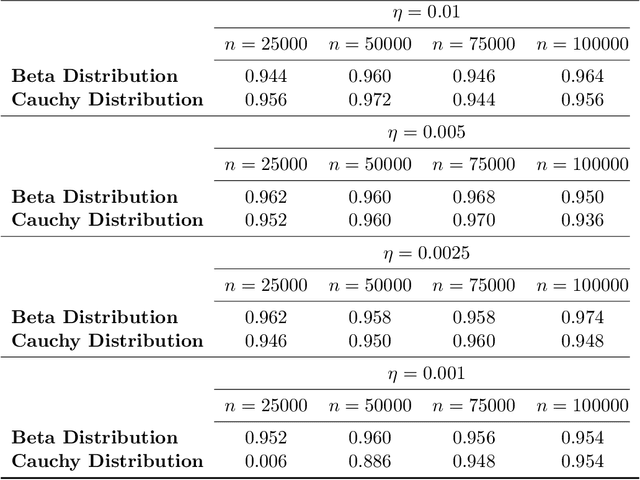
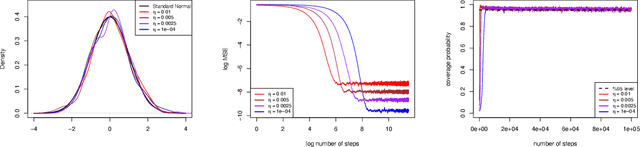
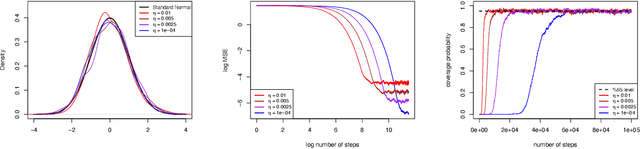
Online Inference for Quantiles by Constant Learning-Rate Stochastic Gradient Descent

This paper proposes an online inference method of the stochastic gradient descent (SGD) with a constant learning rate for quantile loss functions with theoretical guarantees. Since the quantile loss function is neither smooth nor strongly convex, we view such SGD iterates as an irreducible and positive recurrent Markov chain. By leveraging this interpretation, we show the existence of a unique asymptotic stationary distribution, regardless of the arbitrarily fixed initialization. To characterize the exact form of this limiting distribution, we derive bounds for its moment generating function and tail probabilities, controlling over the first and second moments of SGD iterates. By these techniques, we prove that the stationary distribution converges to a Gaussian distribution as the constant learning rate $\eta\rightarrow0$. Our findings provide the first central limit theorem (CLT)-type theoretical guarantees for the last iterate of constant learning-rate SGD in non-smooth and non-strongly convex settings. We further propose a recursive algorithm to construct confidence intervals of SGD iterates in an online manner. Numerical studies demonstrate strong finite-sample performance of our proposed quantile estimator and inference method. The theoretical tools in this study are of independent interest to investigate general transition kernels in Markov chains.