Learning AC Power Flow Solutions using a Data-Dependent Variational Quantum Circuit

Interconnection studies require solving numerous instances of the AC load or power flow (AC PF) problem to simulate diverse scenarios as power systems navigate the ongoing energy transition. To expedite such studies, this work leverages recent advances in quantum computing to find or predict AC PF solutions using a variational quantum circuit (VQC). VQCs are trainable models that run on modern-day noisy intermediate-scale quantum (NISQ) hardware to accomplish elaborate optimization and machine learning (ML) tasks. Our first contribution is to pose a single instance of the AC PF as a nonlinear least-squares fit over the VQC trainable parameters (weights) and solve it using a hybrid classical/quantum computing approach. The second contribution is to feed PF specifications as features into a data-embedded VQC and train the resultant quantum ML (QML) model to predict general PF solutions. The third contribution is to develop a novel protocol to efficiently measure AC-PF quantum observables by exploiting the graph structure of a power network. Preliminary numerical tests indicate that the proposed VQC models attain enhanced prediction performance over a deep neural network despite using much fewer weights. The proposed quantum AC-PF framework sets the foundations for addressing more elaborate grid tasks via quantum computing.

Variational Quantum Eigensolver with Constraints (VQEC): Solving Constrained Optimization Problems via VQE

Variational quantum approaches have shown great promise in finding near-optimal solutions to computationally challenging tasks. Nonetheless, enforcing constraints in a disciplined fashion has been largely unexplored. To address this gap, this work proposes a hybrid quantum-classical algorithmic paradigm termed VQEC that extends the celebrated VQE to handle optimization with constraints. As with the standard VQE, the vector of optimization variables is captured by the state of a variational quantum circuit (VQC). To deal with constraints, VQEC optimizes a Lagrangian function classically over both the VQC parameters as well as the dual variables associated with constraints. To comply with the quantum setup, variables are updated via a perturbed primal-dual method leveraging the parameter shift rule. Among a wide gamut of potential applications, we showcase how VQEC can approximately solve quadratically-constrained binary optimization (QCBO) problems, find stochastic binary policies satisfying quadratic constraints on the average and in probability, and solve large-scale linear programs (LP) over the probability simplex. Under an assumption on the error for the VQC to approximate an arbitrary probability mass function (PMF), we provide bounds on the optimality gap attained by a VQC. Numerical tests on a quantum simulator investigate the effect of various parameters and corroborate that VQEC can generate high-quality solutions.

Data-driven Forced Oscillation Localization using Inferred Impulse Responses

Poorly damped oscillations pose threats to the stability and reliability of interconnected power systems. In this work, we propose a comprehensive data-driven framework for inferring the sources of forced oscillation (FO) using only synchrophasor measurements. During normal grid operations, fast-rate ambient data are collected to recover the impulse responses in the small-signal regime, without requiring the system models. When FO events occur, the source is estimated based on the frequency domain analysis by fitting the least-squares (LS) error for the FO data using the impulse responses recovered previously. Although the proposed framework is purely data-driven, the result has been established theoretically via model-based analysis of linearized dynamics under a few realistic assumptions. Numerical validations demonstrate its applicability to realistic power systems including nonlinear, higher-order dynamics with control effects using the IEEE 68-bus system. The generalizability of the proposed methodology has been validated using different types of measurements and partial sensor coverage conditions.

Scalable Optimal Design of Incremental Volt/VAR Control using Deep Neural Networks

Volt/VAR control rules facilitate the autonomous operation of distributed energy resources (DER) to regulate voltage in power distribution grids. According to non-incremental control rules, such as the one mandated by the IEEE Standard 1547, the reactive power setpoint of each DER is computed as a piecewise-linear curve of the local voltage. However, the slopes of such curves are upper-bounded to ensure stability. On the other hand, incremental rules add a memory term into the setpoint update, rendering them universally stable. They can thus attain enhanced steady-state voltage profiles. Optimal rule design (ORD) for incremental rules can be formulated as a bilevel program. We put forth a scalable solution by reformulating ORD as training a deep neural network (DNN). This DNN emulates the Volt/VAR dynamics for incremental rules derived as iterations of proximal gradient descent (PGD). Analytical findings and numerical tests corroborate that the proposed ORD solution can be neatly adapted to single/multi-phase feeders.

Deep Learning for Optimal Volt/VAR Control using Distributed Energy Resources

Given their intermittency, distributed energy resources (DERs) have been commissioned with regulating voltages at fast timescales. Although the IEEE 1547 standard specifies the shape of Volt/VAR control rules, it is not clear how to optimally customize them per DER. Optimal rule design (ORD) is a challenging problem as Volt/VAR rules introduce nonlinear dynamics, require bilinear optimization models, and lurk trade-offs between stability and steady-state performance. To tackle ORD, we develop a deep neural network (DNN) that serves as a digital twin of Volt/VAR dynamics. The DNN takes grid conditions as inputs, uses rule parameters as weights, and computes equilibrium voltages as outputs. Thanks to this genuine design, ORD is reformulated as a deep learning task using grid scenarios as training data and aiming at driving the predicted variables being the equilibrium voltages close to unity. The learning task is solved by modifying efficient deep-learning routines to enforce constraints on rule parameters. In the course of DNN-based ORD, we also review and expand on stability conditions and convergence rates for Volt/VAR rules on single-/multi-phase feeders. To benchmark the optimality and runtime of DNN-based ORD, we also devise a novel mixed-integer nonlinear program formulation. Numerical tests showcase the merits of DNN-based ORD.

Dynamic Response Recovery Using Ambient Synchrophasor Data: A Synthetic Texas Interconnection Case Study

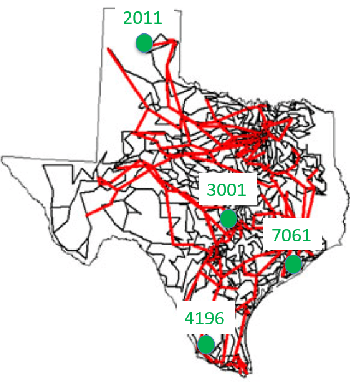
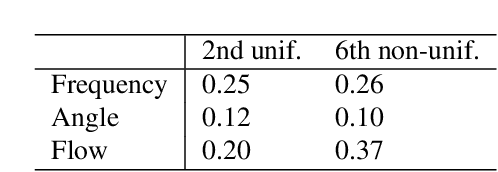
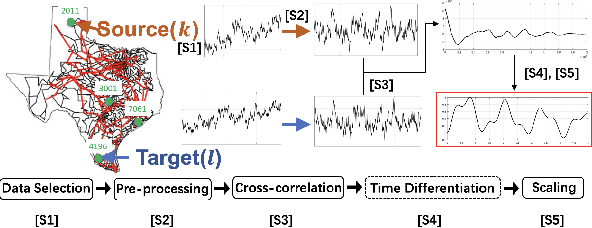
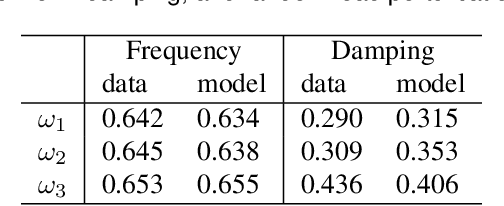
Wide-area dynamic studies are of paramount importance to ensure the stability and reliability of power grids. This paper puts forth a comprehensive framework for inferring the dynamic responses in the small-signal regime using ubiquitous fast-rate ambient data collected during normal grid operations. We have shown that the impulse response between any pair of locations can be recovered in a model-free fashion by cross-correlating angle and power flow data streams collected only at these two locations, going beyond previous work based on frequency data only. The result has been established via model-based analysis of linearized second-order swing dynamics under certain conditions. Numerical validations demonstrate its applicability to realistic power system models including nonlinear, higher-order dynamics. In particular, the case study using synthetic PMU data on a synthetic Texas Interconnection (TI) system strongly corroborates the benefit of using angle PMU data over frequency data for real-world power system dynamic modeling.

Learning Distribution Grid Topologies: A Tutorial

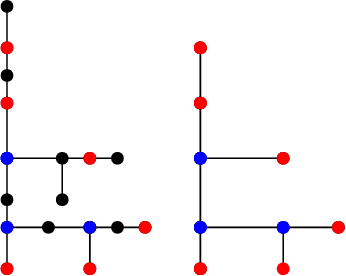
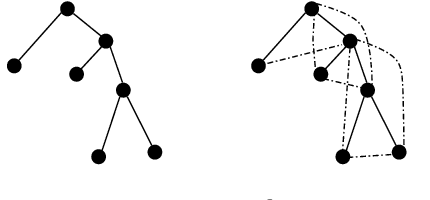
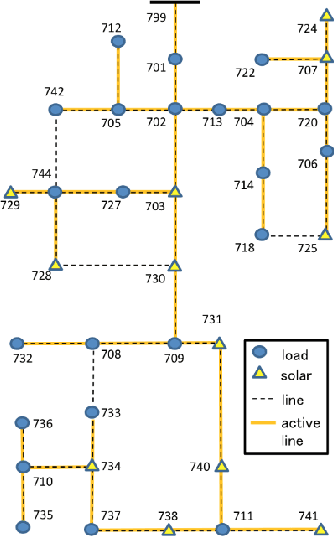
Unveiling feeder topologies from data is of paramount importance to advance situational awareness and proper utilization of smart resources in power distribution grids. This tutorial summarizes, contrasts, and establishes useful links between recent works on topology identification and detection schemes that have been proposed for power distribution grids.% under different regimes of measurement type, observability, and sampling. The primary focus is to highlight methods that overcome the limited availability of measurement devices in distribution grids, while enhancing topology estimates using conservation laws of power-flow physics and structural properties of feeders. Grid data from phasor measurement units or smart meters can be collected either passively in the traditional way, or actively, upon actuating grid resources and measuring the feeder's voltage response. Analytical claims on feeder identifiability and detectability are reviewed under disparate meter placement scenarios. Such topology learning claims can be attained exactly or approximately so via algorithmic solutions with various levels of computational complexity, ranging from least-squares fits to convex optimization problems, and from polynomial-time searches over graphs to mixed-integer programs. This tutorial aspires to provide researchers and engineers with knowledge of the current state-of-the-art in tractable distribution grid learning and insights into future directions of work.

Learning Neural Networks under Input-Output Specifications

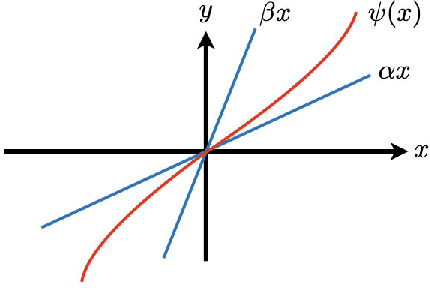
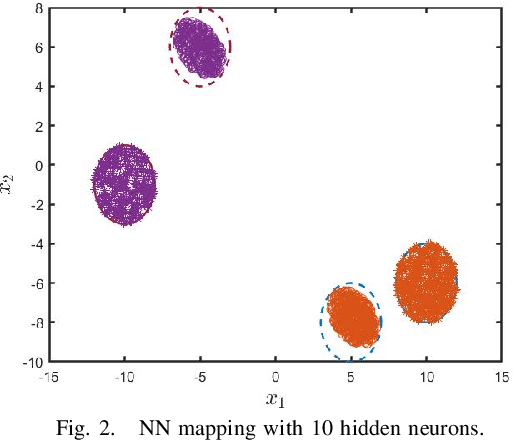
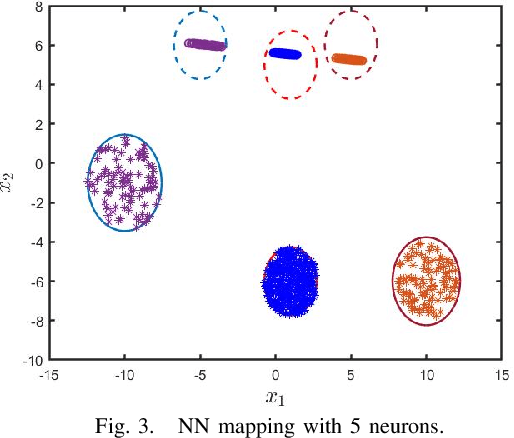
In this paper, we examine an important problem of learning neural networks that certifiably meet certain specifications on input-output behaviors. Our strategy is to find an inner approximation of the set of admissible policy parameters, which is convex in a transformed space. To this end, we address the key technical challenge of convexifying the verification condition for neural networks, which is derived by abstracting the nonlinear specifications and activation functions with quadratic constraints. In particular, we propose a reparametrization scheme of the original neural network based on loop transformation, which leads to a convex condition that can be enforced during learning. This theoretical construction is validated in an experiment that specifies reachable sets for different regions of inputs.

Fast Inverter Control by Learning the OPF Mapping using Sensitivity-Informed Gaussian Processes

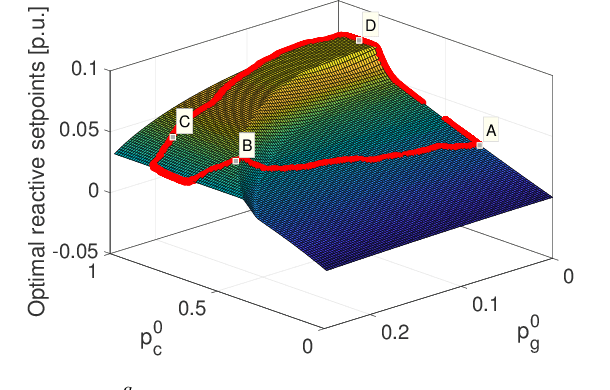
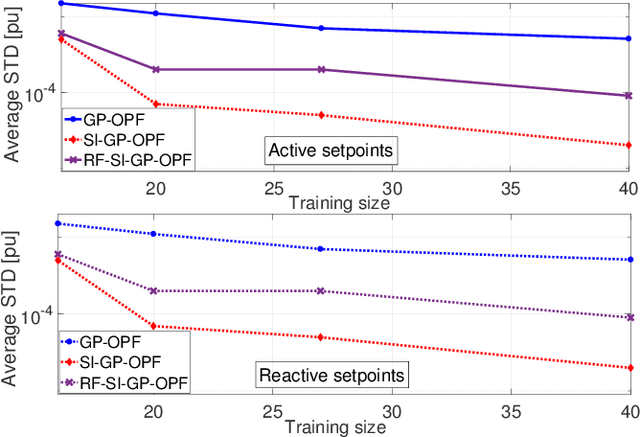
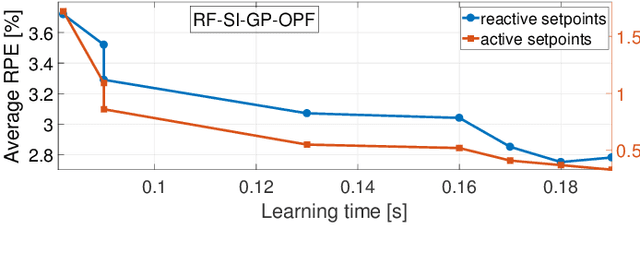
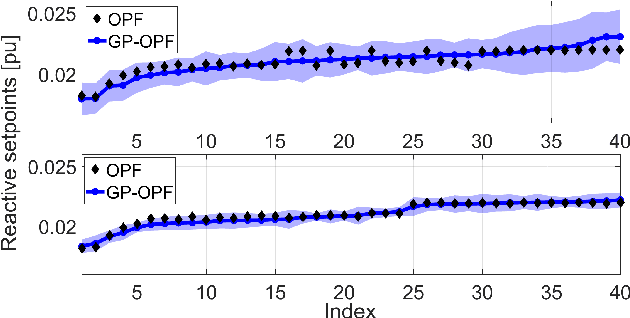
Fast inverter control is a desideratum towards the smoother integration of renewables. Adjusting inverter injection setpoints for distributed energy resources can be an effective grid control mechanism. However, finding such setpoints optimally requires solving an optimal power flow (OPF), which can be computationally taxing in real time. This work proposes learning the mapping from grid conditions to OPF minimizers using Gaussian processes (GPs). This GP-OPF model predicts inverter setpoints when presented with a new instance of grid conditions. Training enjoys closed-form expressions, and GP-OPF predictions come with confidence intervals. To improve upon data efficiency, we uniquely incorporate the sensitivities (partial derivatives) of the OPF mapping into GP-OPF. This expedites the process of generating a training dataset as fewer OPF instances need to be solved to attain the same accuracy. To further reduce computational efficiency, we approximate the kernel function of GP-OPF leveraging the concept of random features, which is neatly extended to sensitivity data. We perform sensitivity analysis for the second-order cone program (SOCP) relaxation of the OPF, whose sensitivities can be computed by merely solving a system of linear equations. Extensive numerical tests using real-world data on the IEEE 13- and 123-bus benchmark feeders corroborate the merits of GP-OPF.

DNN-based Policies for Stochastic AC OPF

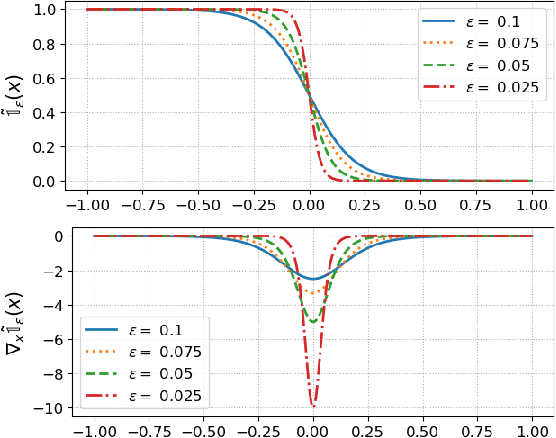
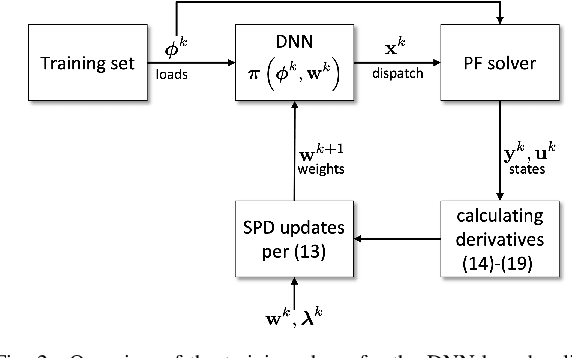
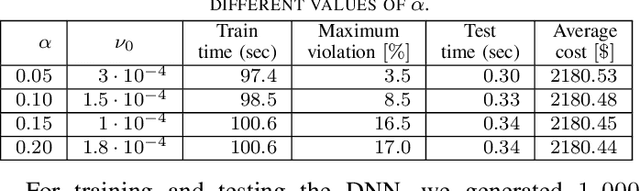
A prominent challenge to the safe and optimal operation of the modern power grid arises due to growing uncertainties in loads and renewables. Stochastic optimal power flow (SOPF) formulations provide a mechanism to handle these uncertainties by computing dispatch decisions and control policies that maintain feasibility under uncertainty. Most SOPF formulations consider simple control policies such as affine policies that are mathematically simple and resemble many policies used in current practice. Motivated by the efficacy of machine learning (ML) algorithms and the potential benefits of general control policies for cost and constraint enforcement, we put forth a deep neural network (DNN)-based policy that predicts the generator dispatch decisions in real time in response to uncertainty. The weights of the DNN are learnt using stochastic primal-dual updates that solve the SOPF without the need for prior generation of training labels and can explicitly account for the feasibility constraints in the SOPF. The advantages of the DNN policy over simpler policies and their efficacy in enforcing safety limits and producing near optimal solutions are demonstrated in the context of a chance constrained formulation on a number of test cases.